Опытная проверка распределения Максвелла: Методические указания к лабораторной работе № 6э по физике

Министерство образования Российской Федерации

Сибирский государственный индустриальный университет

Кафедра общей физики

Опытная проверка распределения Максвелла:

Методические указания к лабораторной работе №6э по физике

          для студентов всех видов обучения всех специальностей

Новокузнецк · 2001

          УДК 533.082 (075.8)

          ОПЫТНАЯ ПРОВЕРКА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА:

Методические указания к лабораторной работе №6э по физике. – Новокузнецк: изд. СибГИУ, 2001. – 15с., рис.6.

            На примере равновесного электронного газа в электронной лампе осуществляется опытная проверка распределения Максвелла. Для проведения эксперимента и обработки экспериментальных данных используется учебно-исследовательский вычислительный комплекс на базе ПК IBM386 и выше.

            Предназначена для студентов всех видов обучения всех специальностей.

          Составили:

          И.Н. Воронов

          С.В. Коновалов

Ó Сибирский государственный индустриальный университет, 2001

Задачи работы:

1. Экспериментально установить вид распределения  электронов по скоростям в вакууме, определить наиболее вероятную скорость  электронов и температуру T электронного газа.

2. Найти функцию распределения F(V) по формуле Максвелла для данной температуры T и представить её графически. Объяснить причины неполного совпадения экспериментальной и теоретической кривых функций F(V) и .

I.  Распределение частиц равновесной макроскопической системы по скоростям теплового движения

Отличительной особенностью любой макроскопической системы является беспорядочное тепловое движение образующих её частиц. Скорости этого движения могут принимать любые значения от нуля до сколь угодно больших. При столкновениях частицы системы обмениваются скоростями, импульсами, энергией. Если система находится в термодинамическом равновесии, то в ней устанавливается не зависящее от времени распределение частиц по скоростям V. Это означает, что в любые два момента времени среднее число частиц dN или доля  их общего числа, скорости которых лежат в данном интервале скоростей dV, одинаково и зависит только от величины этого интервала, его положении на оси скоростей и температуры Tсистемы. Формула, описывающая это распределение, была получена теоретически английским физиком Максвеллом в виде:

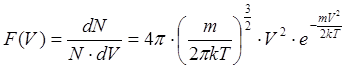.                      (1)

Функция F(V) называется функцией распределения частиц равновесной макроскопической системы по скоростям теплового движения.

В формуле (1):

m –    масса частицы;

T –     абсолютная температура системы;

V –     рассматриваемая скорость;

k –      Дж/К – постоянная Больцмана;

dN –   число частиц, скорости которых лежат в интервале от V до V+dV, т.е. число частиц, скорости которых близки к V;

 - относительное число (доля) частиц, скорости которых лежат в интервале от V до V+dV, или вероятность dP того, что скорость данной частицы лежит в этом интервале;

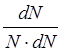 -       плотность вероятности  того, что скорость данной частицы имеет значение в интервале от V до V+dV.

Таким образом, функция распределения Максвелла F(V) есть плотность вероятность того, что скорость данной частицы имеет значение в интервале от V до V+dV.

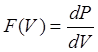
График F(V) изображен на рис.1

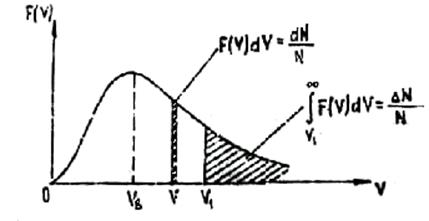
Рис. 1. График функции распределения Максвелла.

Скорость , соответствует максимуму функции F(V), называется наиболее вероятной. Продифференцировав F(V) по скорости V и приравняв полученную производную к нулю,  получим

.

II.  Идеальный газ. Объект исследования

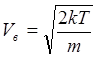Простейшей макроскопической системой является идеальный газ. Это система, для каждой частицы которой выполняется условие:

где      -     среднее время, в течение которого движение частицы можно считать свободным;

          - среднее время, в течение которого частица взаимодействует при столкновении с другой частицей.

          Известным приближением к модели идеального газа может служить облако электронов, испаряющихся при термоэлектронной эмиссии из раскаленной лампы. В данной работе используется пентод 6Ж8.

III.  Идея метода

В пентоде 6Ж8 расположение электронов – анода, катода и трех сеток – цилиндрическое (рис.2). Исследуется равновесное электронное облако, заключенное между катодом и первой сеткой. Концентрация электронов такова, что их длина свободного пробега значительно меньше расстояния между катодом и первой сеткой. В результате многочисленных столкновений электронов друг с другом в этом облаке установится равномерное распределение по направлениям теплового движения (все направления движения равновероятны) и максвелловское распределение по модулям скоростей.

Рис.2. Взаимное расположение катода, одной из сеток катода и анода в пентоде 6Ж8

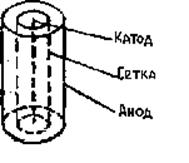
Электронное облако обладает осевой симметрией. Вследствие этого через первую сетку из облака в отсутствие электрического поля в лампе могут пройти лишь те электроны, скорость которых имеют радиальную составляющую , направленную к аноду, т.е. половина их количества.

Поэтому распределение электронов по значениям  описывается выражением типа (1) с той лишь разницей, что числовой коэффициент уменьшается в два раза:

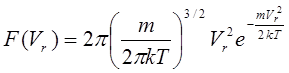                      (2)

На пути электронов, вылетающих из катода, между катодом и первой сеткой создается задерживающее электрическое поле. Преодолеть это поле могут лишь те электроны, у которых радиальная составляющая   скорости удовлетворяет условию

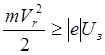
Где     - модуль заряда электрона;

 - задерживающая разность потенциалов между катодом и первой сеткой.

Другими словами, кинетическая энергия таких электронов должна быть больше или равна высоте потенциального барьера , создаваемого задерживающим полем.

Регистрируя зависимость от задерживающего напряжения  относительно числа  электронов, преодолевших задерживающее поле, можно получить экспериментальную кривую функции распределения  для электронов. Как следует из (3), радиальные скорости  электронов, достигших анода, должны превышать минимальное значение :