Определение средней длины свободного пробега и эффективного диаметра молекул воздуха по коэффициенту внутреннего трения: Руководство к лабораторной работе № 5 мол

СИБИРСКИЙ МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ

им. Серго Орджоникидзе

Кафедра физики

Руководство к лабораторной работе № 5 мол

(Молекулярная физика)

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ

СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО

ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА

ПО КОЭФФИЦИЕНТУ ВНУТРЕННЕГО ТРЕНИЯ

Приборы и принадлежности:

1. Сосуд с краном в нижней части и с капилляром, пропущенным через верхнюю пробку.
2. Мензурка мерная на 200 см³ и два химических стакана.
3. Секундомер.
4. Термометр.

Цель работы

Уяснить следующие вопросы:

1.  Что такое средняя длина свободного пробега?

2.  Что называется силой внутреннего трения?

3.  Что называется коэффициентом внутреннего трения и от чего он зависит?

4.  Что называется градиентом скорости?

Краткая теория

Молекулы газа, находясь в непрерывном хаотическом движении, сталкиваются друг с другом. Путь, проходимый молекулой от одного столкновения до другого, называется длиной свободного пробега (l).Так как молекулы движутся хаотически, то длина свободного пробега всякий раз меняется.

Неизменным при данных условиях остается лишь их среднее значение.

(1)

где z - число столкновений,

l - средняя длина свободного пробега молекул.

Кинетическая теория газа устанавливает определенное соотношение между коэффициентом внутреннего трения идеальных газов h, средней длиной свободного пробега молекулы газа l и средней скоростью их движения n. Это соотношение выражается формулой:

(2)

где r - плотность газа при данных условиях.

Более точный вывод соотношения (2), принимающий во внимание распределение скоростей молекул по закону Максвелла, приводит к такому же выражению, только постоянный коэффициент получается другим.

Для воздуха коэффициент пропорциональности принимается равным 1/2. Тогда соотношение (2) примет вид:

отсюда получим:

(2а)

Среднеарифметическая скорость молекул газа определяется по формуле:

(4)

где R – универсальная газовая постоянная,

m - молекулярный вес газа.

Для воздуха m = 29

Плотность газа определяется из уравнения Менделеева – Клапейрона:

(5)

где р - давление, определяемое по барометру,

Т - абсолютная температура газа.

Подставив в уравнение (3) u и r из уравнений (4) и (5), получим:

(6)

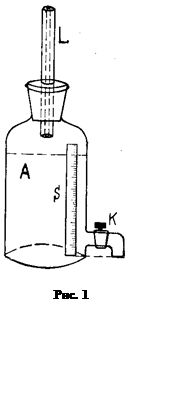Коэффициент внутреннего трения h определяется экспериментально с помощью установки (рис. 1).

При движении слоев газа с различными скоростями между ними возникает сила внутреннего трения, которая ускоряет слой газа, двигающийся более медленно, и замедляет слой, двигающийся с большей скоростью.

Сила трения между слоями газа выражается формулой:

(7)

где  градиент скорости, показывающий величину изменения скорости одного слоя относительно другого, находящегося на расстоянии DZ.

DS - величина площадки соприкасающихся слоев.

Коэффициентом внутреннего трения называется сила внутреннего трения, приходящаяся на единицу площади при градиенте скорости, равном единице.

Для измерения коэффициента внутреннего трения газа используется метод протекания его через капиллярную (узкую) трубку. Объем газа, протекшего через капиллярную трубку, определяется формулой Пуазейля:

(8)

Отсюда получим формулу для определения коэффициента внутреннего трения газа:

(9)

где R - радиус капиллярной трубки,

l - длина капиллярной трубки,

t - время протекания объема газа,

Dр - давление, под которым протекает газ; оно определяется высотой водяного столба.

Экспериментальная часть работы

Сосуд А с краном К в нижней части наполняется водой так, чтобы уровень воды не выходил за пределы шкалы S. Капилляр, пропущенный сквозь пробку в верхней части сосуда, не должен касаться воды. Если открыть кран К, то вода будет вытекать из сосуда под действием разности давлений Dр, равной гидростатическому давлению жидкости, а воздух через капилляр L будет поступать в сосуд А. При этом следует иметь в виду, что правильные результаты эксперимента будут в том случае, если истечение воды определяется диаметром капилляра, а не диаметром отверстия крана. Следовательно, отверстие крана должно быть значительно больше отверстия капилляра.

При закрытом кране К давление воздуха над жидкостью внутри сосуда А равно атмосферному.

Как только открывается кран, начинается истечение жидкости под действием гидростатического давления жидкости, находящейся над уровнем отверстия крана. Непрерывное истечение жидкости будет происходить до тех пор, пока суммарное давление газа и жидкости внутри сосуда на уровне отверстия крана К не станет равным атмосферному, т. е.

где p₁ - давление газа в сосуде в данный момент времени,

h₁ - высота столба жидкости в тот же момент.

При этом на концах капилляра установится разность давлений

обусловливающая протекание воздуха через капилляр в сосуд.

Так как гидростатическое давление мало по сравнению с р_атм, то можно считать, что объем поступающего из атмосферы воздуха DV равен изменению объема в сосуде. По мере поступления воздуха в сосуд вода будет вытесняться из сосуда через кран К сериями капель.

При этом объем протекшего через капилляр газа будет равен объему жидкости, вытекшей, каплями за то же время.

Разность давлении на концах капилляра, равная mgh₁, со временем будет меняться, так как высота столба жидкости будет уменьшаться, но поскольку площадь сечения сосуда велика, а объем вытекающей жидкости сравнительно мал, то изменение h будет незначительное, а, следовательно, и изменение давления Dр будет мало. Поэтому гидростатическое давление Dр можно принять как среднюю разность давлений на концах капилляра в начале и в конце эксперимента:

(10)

где r - плотность жидкости,

g - ускорение силы тяжести.

Для определения Dр нужно: 1) открыть кран К, 2) когда вода станет вытекать сериями капель, подставить стакан, одновременно включить секундомер и произвести отсчет по шкале S высоты h₁, 3) когда в стакане будет 100-200 см³ воды, кран закрыть, одновременно выключить секундомер и произвести отсчет по шкале высоты h₂, 4) произвести отсчет времени и записать, 5) подставить значение h₁ и h₂ в формулу (10) и вычислить Dр, 6) определить объем жидкости с помощью мерной мензурки. Радиус и длина капилляра измерены заранее и указаны на приборе.

Подставив экспериментальные данные в формулу (9), вычислить h. Эксперимент повторить три раза и вычислить среднее значение коэффициента внутреннего трения. Определить абсолютную и относительную ошибки.

По формуле (6) вычислить среднюю длину свободного пробега молекул воздуха.

Известное соотношение

(11)

позволяет вычислить эффективный диаметр (s) молекул газа, если известны l и n - число молекул газа в одном см³ при данных условиях (температуре и давлении).

Из формулы

где k=l,38×10^-16  - постоянная Больцмана.

Подставив значение n в формулу (11) и решив ее относительно s, получим формулу для вычисления эффективного диаметра молекул газа

(12)

Эффективным диаметром молекул газа называется минимальное расстояние, на которое сближаются при столкновении центры двух молекул.

ЛИТЕРАТУРА

1. Фриш С. Э. и Тиморева А. В. Курс общей физики, т. 1,

2. Яворский Б. М. и др. Курс физики, т. 1.

3. Зисман Г. А. и Т оде с О. М. Курс общей физики, т. 1.

4. Савельев И. В. Курс общей физики, т. 1.