Определение средней длины свободного пробега молекул воздуха и коэффициента внутреннего трения (Лабораторная работа № 5мс)

Лабораторная    работа №5мс

ОПРДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА

МОЛЕУЛ ВОЗДУХА И КОЭФФИЦИЕНТА

ВНУТРЕННЕГО ТРЕНИЯ

Краткая теория

Молекулы газа находятся в постоянном и хаотическом движении. Средняя скорость хаотического движения исчисляется сотнями и да­же тысячами метров в  секунду. Но перемещение молекул по объёму происходит с меньшими скоростями. Это вызвано тем, что в процессе хаотического движения происходит постоянное сближение молекул. Сблизившись друг с другом, молекулы под действием сил взаимного отталкивания изменяют направление своего движения. Заметное откло­нение молекул от прямолинейных траекторий при тепловом движении происходит только при их достаточном сближении. Такое взаимодейст­вие между молекулами называется столкновением. Расстояние, кото­рое проходит молекула между двумя последовательными столкновения­ми, назовется длиной свободного пробега. Так как при хаотическом движении соударения носят случайный характер, то длина свободного пробега все время меняется. Поэтому можно говорить только о средней длине свободного пробега.

Молекулярно-кинетичская теория устанавливает определенное соотношение между коэффициентом внутреннего трения, средней длиной свободного пробега молекулы и средней скоростью движения:

                                                                               (1)                                                            

где  - r плотность газа при данных условиях; `l - средняя длина свободного пробега; `v - средняя арифметическая скорость движения молекулы, которая определяется по формуле

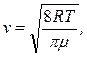                                                                              (2)

где R - универсальная газовая постоянная, m - молекулярная масса газа, для воздуха принимаемая 29 кг/кмоль.

Плотность газа определяется из уравнения Менделеева-Клапейрона:

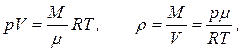                                     (3)

где р - давление, определяемое по барометру; Т - абсолютная тем­пература газа, определяемая по термометру. Из формулы (I) получаем

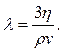
С учётом (2) и (3) среднюю длину свободного пробега можно представить формулой:

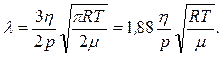                                          (4)

Коэффициент внутреннего трения определяется экспериментально. При движении слоев газа с различными скоростями между ними возникает сила внутреннего трения, которая  ускоряет слой газа, двигаю­щийся более медленно, и замедляет слои, двигающийся с большей скоростью вследствие переноса импульса молекул.

Рассмотрим ламинарное течение воздуха в капилляре. Наличие сил внутреннего трения приводит к возникновению градиента скорос­ти упорядоченного движения . Очевидно, что наибольшая скорость - на оси симметрии капилляра. Вырежем мысленно в газе цилиндрический слой с внутренним радиусом r, внешним радиусом r+dr. На этот слой со стороны более быстрых слоев действует "ускорявшая" сила внутреннего трения

                                                                        (5)

где s - площадь боковой поверхности цилиндра S = 2 prL.

Соотношение (5) можно записать в виде

.                                                                  (6)

Течение воздуха через капилляр радиусом r_o происходит под действием перепада давлений на концах капилляра р₁ – р₂.

Интегрируя (6) по всей площади поперечного сечения (от r = 0 до r = r_o ), получим          

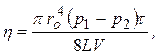                                                            (7)

где V - объём воздуха, протекающий через капилляр (определяет­ся по изменению уровня воды в мерной ёмкости): t - время истече­ния данного объёма воздуха.

Разность давлений на концах капилляра равна

р₁ – р₂ = r_Вg×(h₁ – h₂),                                                           (8)

где h₁ – h₂- разность уровней воls в манометре; r_В - плотность воды; g - ускорение силы тяжести;  r_o, L - радиус и длина капиллярной трубки, соответственно.

Постановка задачи

Используя формулу (7), находим коэффициент внутреннего тре­тий. Зная h, определяем среднюю длину свободного пробега молекул воздуха по формуле (4).                               .

Теория измерений и описание установки

Установка для выполнения работы состоит из двух сосудов, двух клапанов, капилляра и манометра. Схема установки приведена на рисунке.

Мерная ёмкость 4 соединена резиновой трубкой с вспомогатель