Определение логарифмического декремента затухания пружинного маятника и снятие его резонансной кривой: Лабораторный практикум по курсу «Общая физика»

Государственный комитет РФ по высшему образованию

Сибирский государственный индустриальный университет

Кафедра физики

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО

ДЕКРЕМЕНТА ЗАТУХАНИЯ ПРУЖИННОГО

МАЯТНИКА И СНЯТИЕ ЕГО

РЕЗОНАНСНОЙ КРИВОЙ

Лабораторный практикум по курсу «Общая физика»

Новокузнецк 200012001

ТЕОРИЯ  ИССЛЕДУЕМОГО  ЯВЛЕНИЯ

Колебательными называются процессы, точно или приблизительно повторяющиеся через определённый промежуток времени. Теория колебательных процессов важна при расчёте на прочность летательных аппаратов, мостов, отдельных видов машин. Колебательные процессы различной природы описываются одинаковыми уравнениями.

Простейшим типом колебаний являются гармонические колебания, когда координата тела, совершающего свободные колебания, изменяется по закону синуса или косинуса. Зависимость смещения x от времени t материальной точки при гармоническом колебании выражается уравнением:

,                                                                    (1) где – A амплитуда колебания;  - циклическая(круговая) частота свободных колебаний системы; α – начальная фаза колебания; x – смещение.

Гармонические колебания осуществляются под действием квазиупругой силы F

F = -kx,                                                                                              (2)

где k -  коэффициент упругости пружины (коэффициент квазиупругой силы).

,                                                                                         (3)

где m - масса колеблющейся точки (тела).

Собственная круговая частота колебаний  определяется соотношением

.                                                                                   (4)

Если колеблющаяся система находится в вязкой среде, то колебания через некоторое время затухнут (прекратятся). Затухающими называются колебания, энергия которых уменьшается с течением времени. Затухающие колебания совершаются при одновременном действии двух сил: упругой силы и силы сопротивления среды. Уравнение затухающих колебаний имеет вид:

ma = -kx-rv,                                                                                       (5)

где а - ускорение;  kx - возвращающая (упругая или квазиупругая) сила; F = - rv - сила сопротивления среды; г - коэффициент сопротивления; v -скорость движения тела в среде.

Решение уравнения (5) имеет вид:

где  - коэффициент затухания;  - циклическая частота затухающих колебаний системы.

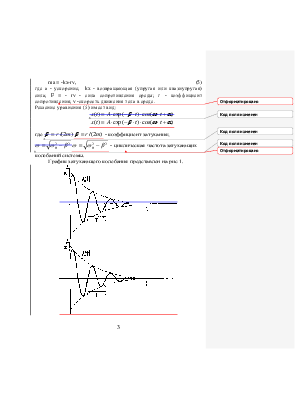
График затухающего колебания представлен на рис 1.

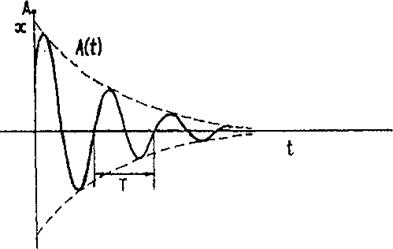
Рис.1. График затухающих колебаний:

А   - амплитуда колебаний в   начальный момент времени;

Т - период колебаний

Логарифмическим декрементом    затухания    называется    логарифм отношения двух последующих амплитуд, отстоящих по времени на период.

             (7)

Для поддержания колебательного процесса приходится прикладывать к системе периодическую внешнюю силу, которая заставляет совершать систему незатухающие вынужденные колебания.

                                                                                   (8)

где F₀ - амплитудное значение внешней вынуждающей силы. Амплитуда вынужденных колебаний системы

                                           (9)

зависит от частоты вынуждающей силы, собственной частоты колебаний и коэффициента затухания β.

Явление резкого возрастания амплитуды вынужденных колебаний, когда частота ω приближается к частоте ω₀ , называется резонансом. При малом коэффициенте затухания β амплитуда вынужденных колебаний достигает очень большой величины.

ЭКСПЕРИМЕНТАЛЬНАЯ  ЧАСТЬ

 Постановка задачи

Задачей эксперимента является:

1. Определение коэффициента упругости. .

2. Определение зависимости периода собственных колебаний пружинного маятника от массы груза и определение частоты собственных колебаний.

3. Определение логарифмического декремента затухания маятника методом сравнения амплитуд.

4. Снятие резонансной кривой колебаний пружинного маятника.

Теория измерений и принципиальная схема установки

Свободные, затухающие и вынужденные колебания можно изучать на пружинном маятнике (рис. 2).

Он состоит из спиральной пружины, на нижнем конце которой подвешен груз массой m. Если вывести маятник из положения равновесия, то он будет совершать свободные затухающие колебания. Маятник может также совершать и вынужденные колебания. Для их получения верхний конец пружинного маятника прикрепляется к нити, которая перекинута через блок и присоединена к эксцентрику, вращаемому электродвигателем. Вращение двигателя с частотой ω передается грузу, который представляет собой тело обтекаемой формы. Это предотвращает возникновение вихревых движений в среде. Груз под влиянием вынуждающей силы (двигателя) придет в колебательное движение с частотой .

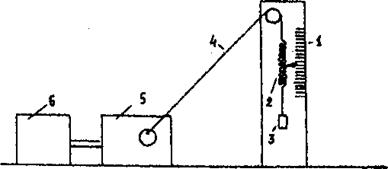
Рис.2. Пружинный маятник:

1 - шкала;  2 - пружина;  3  - груз;   4  - нить, связанная с эксцентриком; 5 - редуктор; 6 - электродвигатель

Он состоит из спиральной пружины, на нижнем конце которой подвешен груз массой m. Если вывести маятник из положения равновесия, то он будет совершать свободные затухающие колебания. Маятник может также совершать и вынужденные колебания. Для их получения верхний конец пружинного маятника прикрепляется к нити, которая перекинута через блок и присоединена к эксцентрику, вращаемому электродвигателем. Вращение двигателя с частотой ω передается грузу, который представляет собой тело обтекаемой формы. Это предотвращает возникновение вихревых движений в среде. Груз под влиянием вынуждающей силы (двигателя) придет в колебательное движение с частотой .