ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПРОВОДИМОСТИ ПОЛУПРОВОДНИКА, ПОСТОЯННОЙ ХОЛЛА, ПОДВИЖНОСТИ НОСИТЕЛЕЙ ТОКА
Целью данной работы является определение постоянной Холла, определение знака и концентрации носителей тока, удельной проводимости и удельного сопротивления материала образца.
Рассмотрим однородную проводящую пластину, к граням АА’ и СС ' которой приложена некоторая разность потенциалов.
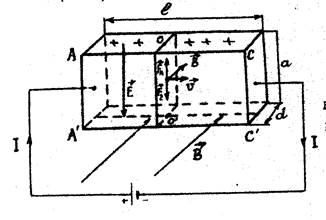
Рис.1. Схема возникновения поперечной разности потенциалов в проводящем образце.
В проводнике возникает электрический ток. При отсутствии магнитного поля потенциалы в симметричных точках, например, О и О`, одинаковы. Если же пластину с током поместить в магнитное поле, направленное перпендикулярно боковым граням (см. рис.1), то между точками О и О` возникает разность потенциалов U. Наблюдаемое явление называется эффектом Холла, а возникающая "поперечная" разность потенциалов — холловским напряжением.
Опытным путем установлено, что возникающая разность потенциалов
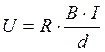 (1)
(1)где R - коэффициент пропорциональности (коэффициент Холла), зависящий от материала пластины;
B-индукция магнитного поля;
I- ток в образце;
d - толщина пластины.
Явление Холла можно объяснить следующим образом. Пусть ток I в пластине обусловлен движением положительных зарядов q , концентрация которых n , а средняя скорость упорядоченного движения V. Тогда сила тока I выразится формулой
![]() (2)
(2)
где S - площадь поперечного сечения пластины.
При наложении магнитного поля, индукция которого равна B на каждый носитель тока действует сила Лоренца, равная
![]() (3)
(3)
в направлении вверх (см. рис. 3).
В результате на верхней грани пластины образуется избыток положительных зарядов, а вблизи нижней грани — их недостаток. Таким образом, в пластине возникает поперечное электрическое поле с напряженностью Е. Это поле действует на носители тока с силой.
![]() ,
(4)
,
(4)
направленной противоположно силе Лоренца. Когда электрическое поле уравновесит силу Лоренца, наступит динамическое равновесие, и между гранями пластины установится холловская разность потенциалов U
Из уравнений (3) и (4) следует, что
![]() (5)
(5)
и численное значение напряженности электрического поля будет
![]() .
(6)
.
(6)
Полагая поперечное электрическое поле однородным, можно записать:
![]() .
(7)
.
(7)
Подставляя в формулу (7) выражение из (2), имеем:
![]()
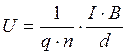 . (8)
. (8)
Таким образом, полученный результат совпадает с экспериментальной формулой (1) и (8) следует, постоянная Холла имеет следующее значение:
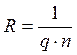 (9)
(9)
Величина R зависит от материала пластины, а ее знак совпадает со знаком заряда q носителей тока. При электронной проводимости R<0, при дырочной R>0.
Зная R , можно также определить концентрацию носителей тока, если известен заряд носителей:
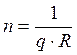 .
(10)
.
(10)
Важными характеристиками проводников и полупроводников являются удельная проводимость s, подвижность m и удельное сопротивление r. Покажем, как, зная постоянную Холла, определить эти характеристики вещества. Плотность электрического тока в образце согласно закону Ома в дифференциальной форме
![]() ,
(11)
,
(11)
где s- удельная проводимость;
E - напряженность электрического поля вдоль образца (направление А — С). (см. рис. 1)
Значение тока в образце
![]() .
(12)
.
(12)
Считая продольное электрическое поле внутри образца однородным, можем выразить Е через напряжение на образце (между, точками А и С) и длину образца l:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.