Определение показателя адиабаты воздуха методом Клемана-Дезорма: Методические указания к выполнению лабораторной работы

Министерство образования Российской Федерации

Сибирский государственный индустриальный университет

Кафедра физики

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА

Методические указания к выполнению лабораторной работы

по курсу «Общая физика»

Новокузнецк

2001

УДК 531

О62

Рецензент

Кандидат технических наук, доцент каф. физики металлов СибГИУ

Н. Н. Кушнаренко

Определение показателя адиабаты воздуха методом Клемана-Дезорма: Метод, указ. / Сост.: Е.А. Будовских, В.А. Петрунин, Н.Н. Назарова, В.Е. Громов: СибГИУ.- Новокузнецк, 2001.- 13с.

В работе определяется показатель адиабаты воздуха, скорость звука в нем и молярные величины внутренней энергии и энтальпии. Непосредственно измеряются: начальное избыточное давление газа в сосуде; время, в течение которого газ находится при постоянном давлении после адиабатического расширения при открытом кране сосуда; соответствующее этому времени избыточное давление, воз­никающее в сосуде после закрытия крана при изохорном нагреве. Измерения проводятся при различных значениях времени.

Работа предназначена для студентов всех специальностей.

ПОСТАНОВКА ЗАДАЧИ

При изменении состояния термодинамической системы в общем случае меняется и ее температура.

Величина С, определяемая формулой

D =CdT

когда приток тепла dQ отнесен к одному молю системы, называется мо­лярной теплоемкостью. Её значение зависит от вида процесса изменения состояния. При адиабатическом процессе в теплоизолированной системе, когда dQ = 0, теплоемкость равна нулю. Если состояние изменяется изо­термически (dТ = 0), то теплоемкость равна бесконечности.

Согласно первому началу термодинамики подводимое к системе те­пло dQ в расчете на один моль в процессе малого изменения его состоя­ния связано с изменением внутренней энергии системы dU и работой рdV , совершаемой системой, соотношением

DQ = dU + pdV

Где p - давление;

V- молярный объем.

Из этого уравнения следует, что при изохорическом изменении со­стояния (dV = 0)

           

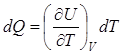
Соответствующая теплоемкость 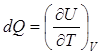 называется теплоемкостью при постоянном объеме.

Помимо внутренней энергии в термодинамике используется еще од­на важная для ряда практических приложений функция состояния I, назы­ваемая теплосодержанием или энтальпией,

            I = U + pV,

или

                       

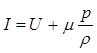
где m - молярная масса;

r - плотность системы. При изобарическом изменении состояния, когда dp=0,

                       

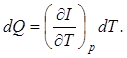
Величина 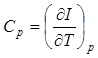 называется теплоемкостью при постоянном давлении.

Таким образом, если объем системы остается постоянным, то приток тепла равен приращению внутренней энергии системы, если же постоянно давление, то он выражается приращением энтальпии.

Так как для идеального газа I = U(T) + pV, то теплосодержание та­кого газа, как и его внутренняя энергия, есть функция только температуры. Теплоемкости С_p и С_V идеального газа и их отношение g = C_p/C_V тоже зависят только от температуры; при этом

                        C_p – C_V =R,

где R - универсальная газовая постоянная.

Так как R > 0 и С_V > 0, то всегда g > 1.

Согласно классическому результату статистической физики энергия молекул газа, находящегося в равновесном состоянии, распределяется одинаковыми долями по всем степеням свободы возможных движений молекулы. Энергия, приходящаяся на одну степень свободы, составляет в расчете на один моль . Таким образом, если i - число степеней свободы движения молекулы, внутренняя энергия одного моля газа U равна

                                   

С учетом уравнения состояния pV = RT  молярное теплосодержание идеального газа

                       

Соответственно теплоемкости С_p и С_V и их отношение у даются формулами

Таким образом, теплоемкости находящегося в равновесном состоя­нии идеального газа с равномерным распределением энергии по степеням свободы постоянны.

Наименьшее число степеней свободы - три - имеют одноатомные га­зы (при нормальных условиях - это гелий Не, неон Nе и др., при высокой температуре - полностью диссоциированные кислород О, азот N и др.). Для таких газов g = 5 / 3, и это значение хорошо подтверждается экспери­ментальными данными. Газы с очень сложными молекулами имеют боль­шое число внутренних степеней свободы и для них g® 1. Таким образом, величина g для идеальных газов заключена в пределах 1 < g < 5 / 3.

Классический результат статистической физики не дает правильного представления о распределении энергии по колебательным степеням сво­боды молекул, а при очень низких температурах - и по вращательным сте­пеням свободы молекул. Так, для двухатомной молекулы (О₂, Н₂ и др.) число степеней свободы i = 7 (три поступательных, две вращательных -вокруг главных осей, две колебательные - симметричные и антисиммет­ричные колебания вокруг центра масс), и согласно классической теории g =9/7.

Однако, как следует из квантовой теории, теплоемкости двухатом­ных молекул при постоянном объеме

при Т<<q                              и  

            при Т>>q                                и    

где q - характеристическая колебательная температура (q для кисло­рода равна 2273 К, для азота - 3393 К).

Таким образом, отношение теплоемкостей у двухатомных газов при нормальной температуре с большой точностью равно 7/5 и, постепенно уменьшаясь с ростом температуры, лишь при температуре в несколько ты­сяч градусов (меньшей, чем температура, при которой существенную роль начинает играть диссоциация) приближается к значению 9/7, следующему из классической теории.

У воздуха, представляющего собой в основном смесь двухатомных газов - азота и кислорода, значения у при нормальных условиях близки к 7/5, т.е. 1,40.