Определение показателя адиабаты воздуха методом Клемана-Дезорма: Методические указания к выполнению лабораторной работы, страница 2

Для идеального газа с постоянными теплоемкостями

U = C_V×T,                            I = C_p×T.

Пользуясь приведенными выше соотношениями, выражениям для U и / можно придать вид

           

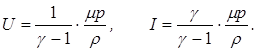
Точное измерение величины C_V затруднительно. Практически удоб­нее измерить величину C_p и g, а теплоемкость вычислить по формуле С_V = С_p /g. Кроме того, отношение теплоемкостей играет большую роль при процессах близких к адиабатическим. В частности, от него зависит скорость звука в газовых средах, параметры течения газов со звуковыми и сверхзвуковыми скоростями по трубам и в соплах.

При адиабатическом обратимом процессе термодинамические пара­метры р и V связаны уравнением Пуассона

           

В дифференциальном виде оно имеет вид

            g×p×dV + V×dp = 0                                                                       (1)

В связи с этим g называют показателем адиабаты.

Скоростью звука  V_ЗВ называют скорость, с которой распространяются в сжимаемых средах ма­лые возмущения давления, и, в частности, звуковые волны.

Характерные значения скорости, с которой звук распространяется в нормальных условиях, для большинства реальных сред лежат в следую­щих пределах: для газов и паров - от 150 до 1000 м/с, для жидкостей от 750 до 2000 м/с, для твердых тел от 2000 до 6000 м/с.

Внутреннюю энергию и теплосодержание идеального газа можно выразить через скорость звука:

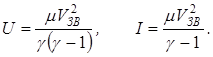                                                       (3)

Задачей данной работы является измерение величины отношения теплоемкостей воздуха, скорости звука и молярных величин внутренней энергии и энтальпии.

ТЕОРИЯ МЕТОДА И ОПИСАНИЕ УСТАНОВКИ

Измерения проводятся по методу, предложенному Клеманом и Дезормом (1819 г.). Стеклянный баллон вместимостью в несколько литров (рисунок 1) наполняют воздухом при атмосферном давлении. С помощью насоса в баллон дополнительно накачивают небольшую порцию воздуха, затем кран k₁ закрывают. Спустя несколько минут температура газа в бал­лоне сравнивается с температурой t₀ окружающего воздуха. После этого водяным манометром измеряют давление р₁ газа в баллоне. Затем на ко­роткое время открывают кран К₂ . При этом часть воздуха выходит из бал­лона, и его давление сравнивается с атмосферным р₀. Газ, оставшийся в баллоне, адиабатически расширяется, вследствие чего его температура по­нижается до значения Т₂. Затем кран К₂ закрывают и газ начинает мед­ленно нагреваться, пока его температура не

сравнивается с температурой Т₀ , при этом давление становится равным р₂. По измеренным давлениям р₁ и р₂ можно вычислить отношение теплоемкостей g.

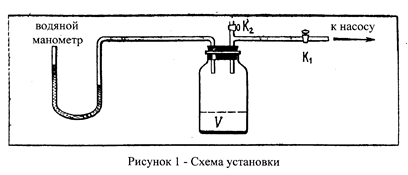Для того, чтобы показать это, мысленно выделим внутри баллона произвольную порцию воздуха, ограниченную замкнутой поверхностью объёмом V (рисунок 1). В моменты отсчётов давления параметры, харак­теризующие состояние газа внутри поверхности, имеют следующие значе­ния:

1-е состояние: р₁, T₀, V₁;

2-е состояние: p₀, T₂, V₂;

3-е состояние: р₃, T₀, V₂.

Разности давлений р₁ – р₀ и р₃ – р₁ в сотни и тысячи раз меньше атмосферного давления p₀, а поэтому для упрощения вычислений с этими разностями можно обращаться как с бесконечно малыми дифференциала­ми. То же относится к соответствующим изменениям объема выделенной порции воздуха. Переход газа из состояния 1 в состояние 2 совершается адиабатически и соответствующие изменения давления и объема связаны уравнением адиабаты (1). Полагая в нем dV = V₂ – V₁, dp = p₀ – р₁, можно записать

gp(V₂ – V₁) + V(p₀ – p₁) = 0.                                                       (4)

В состояниях же 1 и 3 температуры газа одинаковы, и поэтому в этих состояниях произведение pV одно и то же (pV = const). Следова­тельно

PdV + Vdp =0,