Определение показателя адиабаты воздуха методом Клемана-Дезорма: Методические указания к выполнению лабораторной работы, страница 3

Или

p(V₂ – V₁) + V(p₃ – p₁) = 0                                                         (5)

Из соотношений (4) и (5) можно получить, что

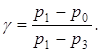
В эту формулу входит отношение разностей давлений, которые удобно измерять в миллиметрах водяного столба с помощью манометра (рисунок 1).

Обозначая разности давлений р₁ – p₀ и р₃ – p₀ как разности уров­ней в коленах манометра Н и h₀ соответственно, последнюю формулу можно записать в виде

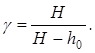                                                                                (6)

Для того, чтобы точно измерить g с использованием этой формулы, кран К₂ надо закрыть именно в тот момент, когда произойдет выравнива­ние давления воздуха внутри и вне сосуда. Время t , при котором кран К₂ должен оставаться открытым, с одной стороны, мало, а с другой - неиз­вестно. Поэтому, если кран К₂ закрыть раньше, чем произойдет выравни­вание давлений, то измеренное значение h₀ окажется завышенным, а, сле­довательно, значение g - заниженным. Если же кран закрыть позже, то по­лучится завышенное значение g.

С тем, чтобы повысить точность измерений, время выдержки t при открытом кране К₂ можно заведомо увеличить по сравнению с малым временем выравнивания давлений. При этом будет происходить теплооб­мен, в процессе которого относительная скорость уменьшения разности температур Q = Т₂ – T₀ адиабатически охлажденного воздуха и комнатной T₀ будет оставаться постоянной:

Эта скорость т, с^-1 называется темпом нагрева. Её величина зависит от физических свойств системы, её формы и размеров, а также коэффици­ента теплоотдачи.

Из последнего уравнения следует, что

,

где Q₀ = T₂ – T₁ разность температур сразу после адиабатического расширения, когда t = 0.

Соответствующую ей разность давлений в формуле (6) можно най­ти, пользуясь тем, что после закрытия крана К₂ процесс теплообмена будет продолжаться изохорически. Следовательно, измеряемое повышение дав­ления h после его окончания будет изменяться по закону

или

ln h = ln h₀ - mt ,                                                            (7)

где h - измеряемое давление, соответствующее времени t.

 Тогда, построив график линейной зависимости (7), значение h₀ можно найти по значению In h₀ , проэкстраполировав график до пересече­ния с осью ординат.

При таком способе измерения величины h₀ необходимо несколько раз провести измерения величин h, соответствующих различным момен­там времени t, каждый раз обеспечивая одну и ту же разность давлений H. Практически же сделать это с помощью ручного насоса не удается. Неточ­ное воспроизведение давления Н является еще одним источником ошибок при определении величины g, который необходимо учесть.

В связи с этим представим выражение (6) в виде

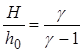
 или с учетом зависимости (7) как

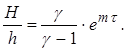
После его логарифмирования будем иметь

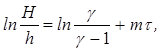
т. е. линейное уравнение

y=a+mt,                                                                                      (8)

где , а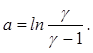  

Отсюда

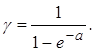                                                                                        (9)

При этом ошибка определения у с использованием формулы для ошибок косвенных измерений может быть записана в виде

                                                                 (10)

где у - среднее значение у, рассчитанное по средним значениям `а и `m.

 Значения констант `а и `m можно определить аналитически путем ап­проксимации прямой (8) методом наименьших квадратов, который обес­печивает минимум ошибок.

Для рассматриваемой задачи оценки значений `а и `т по набору экспериментальных точек (t₁,y₁), ... , (t_N , y_N) могут быть найдены по формулам

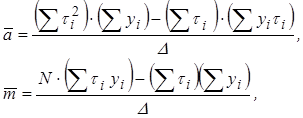                                (11)