Измерение момента инерции маховика методом маятника Максвелла: Методические указания и выполнению лабораторной работы

Министерство Образования РФ

Сибирский государственный индустриальный университет

ИЗМЕРЕНИЕ  МОМЕНТА ИНЕРЦИИ МАХОВИКА  МЕТОДОМ МАЯТНИКА МАКСВЕЛЛА

(Методические указания и выполнению лабораторной работы по курсу "Общая физика")

Издание СМИ                                                     Новокузнецк 1983

УДК  53(075)

Работа проводится по теме "Динамка поступательного и вращательного движений".

Наложена теория колебаний маятника Максвелла. Предлагается метод измерения момента инерции маховика, основанный на теории колебаний маятника Максвелла.

ПРИБОРЫ  И ПРИНАДЛЕЖНОСТИ

Маятник Максвелла, линейка, секундомер.

ТЕОРИЯ КОЛЕБАНИЙ МАЯТНИКА МАКСВЕЛЛА

Цель работы - уяснить теорию колебаний маятника Максвелла, т.е. законы, на которых она построена: законы изменения и сохранения энергии, законы Ньютона, законы изменения и сохранения  импульса и момента импульса системы,  измерить момент инерции махо­вика методом маятника Максвелла, т.е. используя теорию  колебаний маятника Максвелла.

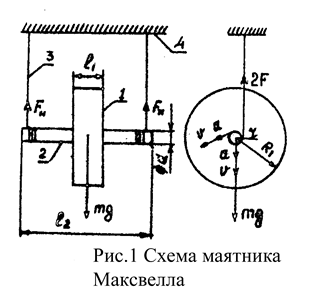
Маятник Максвелла (рис. I) представляет собой маховик 1 с уд­линенной осью 2, висящей на равнодлинных нитях 3.

Накручивая натянутые ни­ти на осевой стержень, мы за­ставляем маховик подняться на высоту Н₁. Представленный самому себе, он, вращаясь, опускается вниз. По мере опу­скания скорость маховика воз­растает. Наконец, нити пол­ностью сматываются со стерж­ня. Маховик проходит нижнее положение ( Н₀ = 0) и,  вращаясь по инерции, накручивая нити на осевой стержень, поднимается вверх на высоту Н₂ ( Н₂<H₁ ).

Затем все повторяется в статном порядке. После  повторного прохождения нижнего положения маховик поднимается на высоту Н₃ (Н₃ < Н₁). Таким образом, маятник совершает колебания с периодом  Т и амплитудой Н.

При движении вниз потенциальная энергия маховика переходит в кинетическую энергию покупательного и вращательного движений. В нижней точке под действием нитей импульс маховика меняется на обратный, но сохраняется момент импульса. При движении вверх кинетическая энергия поступательного и вращательного движений переходит в потенциальную.

Наблюдающееся за период уменьшение амплитуды на  DН = Н₁-Н₂ связано с переходом механической энергии во внутреннюю через  работу сил трения и сопротивления (нагрев нитей, маховика, воздуха, несущей конструкции).

Выражение для момента инерции без учете рассеяния энергии

На маховик действуют нити с силой F_н каждая и сила тяжести

P=mg (рис. 2).

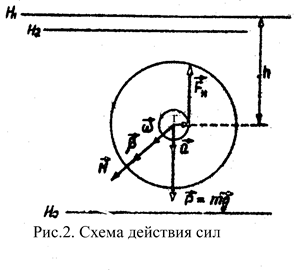
   Для поступательного и вращательного движений в соответствии с основными законами имеем

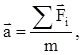                    (1)

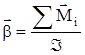,                  (2)

где а и b  - линейное и угловое ускорения; åF_i и åM_i - результирующие сила и момент силы; m и Á - масса  и момент инерции маховика.

В проекциях на направление скорости и ось

                                                                           (3)

                                                                            (4)

где r-радиус осевого стержня.

Для сматывания нитей без проскальзывания и без учета растяжения нитей

V =w×r                                                                                     (5)

где v и w  - скорости поступательного и вращательного движений маховика, и  для тангенциального и углового ускорений получаем                                       

             a=b×r                                                                                          (6)

Из (3):

                                                                                        (7)

из (4),(6)и (7):

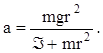                                                                              (8)

Для заданных m, g, r, Á a=const, и закон движения (от Н₁ до Н₀) принимает вид: 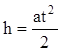 или о учетом (8)

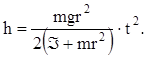                                                                          (9)

 Последнее выражение может быть использовано для косвенного измерения момента инерции, откуда

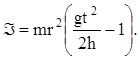                                                                             (10)

  Формула (10) находится в соответствии о законом сохранения механической энергии ( DП = - DТ), по которому

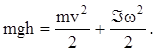                                                                           (11)

Состояния маховика указаны на ряс. 2; изменением энергии нитей  и энергии деформации несущей конструкции маятника пренебрегаем,

Учитывая, что 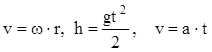 из (11) получаем (10).