Измерение момента инерции маховика методом маятника Максвелла: Методические указания и выполнению лабораторной работы, страница 2

Теоретический момент инерции маховика

  По определению момент инерции система           

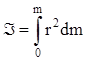                                                                              (12)

зависит от массы и ее распределения около оси вращения, характеризует инерциальные свойства тела. Для заданной оси он может быть рассчитан теоретически при известных форме, размерах и плотности.

Интеграл (12) для исследуемого маховика дает следующее выражение:

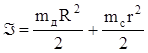    ,                                                               (13)

где m_д и r - масса и радиус диска; r и m_c - радиус и масса осевого стержня вне диска (рис. I).

Массы m_д и m_c находятся по определению плотности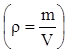

через объемы:

m_д = r×V_д = rpR²l₁;                                                       (14)

m_c = r×V_c = rpr² (l₂ - l₁),                                                          (15)

где r - плотность материала маховика (сталь, r = 7,8×10³ кг/м³);

 l₁ - толщина диска;                          

 l₂ - длина осевого стержня.

Сила натяжения нитей при прохождении нижнего положения

маховика

При падении с высоты Н за время t и полном сматывании  ни­тей скорость маховика достигает максимального значения

В первом приближении изменение импульса маховика на обратный происходит за время перехода его из положения 1 в положение 2 (рис. 3) вращением вокруг конца нити  О с линейной скоростью цент-

ра

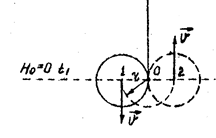       Для оценки можно  принять время перехода из 1 в 2 (время рывка):

На основании закона изменения импульса системы:

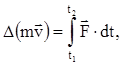
                             (16)

В проекции  на вертикальное направление

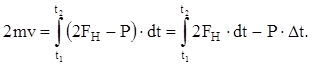                             (17)

Если F^’_H – средняя сила за время Dt ,то

           

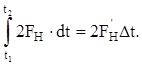
Из (17):

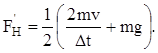                                                                            (18)

С учетом   ,  имеем:

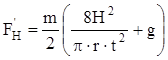            .                                                             (19)

В случае покоящегося подвешенного маховика сила натяжения каждой нити

                                                                                               (20)

ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ

1. Измерьте радиус осевого стержня, толщину, и радиус диска, массу маховика (рис. 1).

2. Возьмите маховик двумя руками за концы осевого стержня и, слегка натягивая нити, намотайте их виток к витку по направлению к центру маховика.

3. Замерьте высоту Н₁, на которую поднялся маховик в  результате накручивания нитей.          

4. Замерьте время движения маховика до нижней точки, повто­рив измерения три раза для одного и того же Н₁.

  5. Рассчитайте среднее значение  момент инерции, используя формулу (10) и доверительный интервал, принимая  g = 9,8 м/с².

6. Рассчитайте момент инерции маховика по формуле (13).

7. Сопоставьте моменты инерции по пунктам 5 и 6 и объясните различие, если. таковое имеется.

8. Рассчитайте среднюю силу натяжения нитей при рывке по формуле (19), при падении с высоты Н до нижнего положения по формуле (18), при покоящемся маховике по формуле (20) и сравните их.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Основные законы динамики поступательного и вращательного движений.

2. Законы сохранения импульса, момента импульса, механической  энергии.

3. Чем определяется  и что характеризует момент инерции?

4. Какие сделаны допущения (чем пренебрегается) при выводах формул (10) и (19)?    

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Савельев И.В. Курс общей физики. – М.: Наука, 1977.

Ч.1. - 416с., ил.

2.Путилов К.А. Курс физики. - М.: Физматгиз,  1963. Т.1.-487с.,ил.

3. Физический практикум. /Под ред. В.И.Ивероновой. - М.:  Наука, 1967. - 352 с., ил.

 4. Определение моментов инерции оборотного маятника и маятника Максвелла. /Под ред. А.В.Росторгуевой. -М.: Изд. Московского высшего технического училища им.Баумана. 1980. - 10 с., ил.

Составители:

Семен Борисович Быков,

 Владимир Никитович Березовский

ИЗМЕРЕНИЕ  МОМЕНТА ИНЕРЦИИ МАХОВИКА  МЕТОДОМ МАЯТНИКА МАКСВЕЛЛА

(Методические указания и выполнению лабораторной работы по курсу "Общая физика")

Утверждены на заседании кафедры физики 26 марта 1983 г., протокол  № 241, и одобрены методической  комиссией

Редактор Калинина Н.П.

Сибирский металлургический институт, 654053 Новокузнецк, ул. Кирова, 42. Лаборатория оргтехники СМИ