Министерство высшего и среднего специального образования РСФСР
Сибирский ордена Трудового Красного Знамени металлургический институт имени Серго Орджоникидзе
ИЗМЕРЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕКМОСТИ ВОЗДУХА
ПРИ ПОСТОЯННОМ ДАВЛЕНИИ К ЕГО ТЕПЛОЕМКОСТИ
ПРИ ПОСТОЯННОМ ОБЪЕМЕ
Лабораторный практикум по курсу "Общая физика"
Издание СМИ Новокузнецк 1969
УДК 533.7:536.63
Рассмотрен метод Клемана-Дезорма. для определения показателя адиабаты газа.
Работа предназначена для студентов всех специальностей дневного, вечернего и заочного обучения.
Рецензент - кафедра высшейматематики Сибирского металлургического института(зав. кафедрой Галкин В.П,).
Печатается по решению редакционно-издательского coветa института, протокол №5 от 7 февраля 1989 г.
Задачей эксперимента является измерение отношения теплоемкости воздуха при постоянном давлении к его теплоемкости при постоянном объеме.
Для измерения предлагается метод адиабатического расширения газа с последующей изохорической выдержкой.
Теплоемкостью тела называется физическая величине, числено равная количеству теплоты, которое необходимо сообщить телу, чтобы повысить его температуру на один градус.
Теплоемкость единицы массы называется удельной теплоемкостью, в теплоемкость одного моля вещества - молярной теплоемкое ты». Таким образом,
 |
Молярная к удельная теплоемкости связаны соотношением
Сm =m×с.
Величина теплоемкости вещества зависит от условий нагревания и температуры.
Рассмотрим теплоемкости идеального газа при его изобарическом (P=const) и изохорическом (V=const) нагревании.
Из первого начала термодинамики следует, что подведенная к газу теплота dQ расходуется на увеличение его внутренней энергии dU и на совершение работы против внешних сил dA:
dQ = dU + dA. (3)
Изменение внутренней энергии идеального газа равно
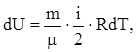 (4)
(4)
где i - число степеней свободы. (Число независимых координат, однозначно определяющих положение частицы в пространстве. Для одноатомных молекул i = 3; двухатомных - i = 5; многотомных - i = 6).
Для изобарического процесса
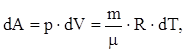 (5)
(5)
тогда из уравнений (3)-(5) имеем:
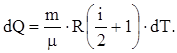
Для изохорического процесса dA=0.
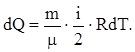 (6)
(6)
Из (2), (5) и (6) имеем:
![]() (7)
(7)
![]() (8)
(8)
отношение теплоемкостей
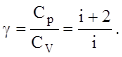 (9)
(9)
Таким образом, теплоемкость идеального газа не зависит от температуры и является функцией процесса.
Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой (dQ=0). Описывается он уравнениями Пуассона:
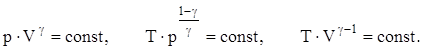 (10)
(10)
Поэтому g называют еще коэффициентом Пуассона или показателем адиабаты.
Идеальная теплоизоляция системы невозможна. В этом смысле адиабатический процесс является реальным. Быстрые реальные процессы можно считать адиабатическими (теплообмен не успевает происходить в заметной степени).
Показатель адиабаты, рассчитанный по формуле (9) через степени свободы, назовем теоретическим, а измеренный с использованием уравнений Пуассона (10) - экспериментальным.
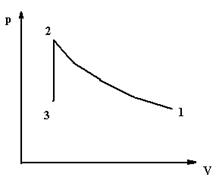 |
Рис.1. Закачивание воздуха в сосуд и его
изохорическая выдержка
Процесс закачивания (1®2) может быть близким к адиабатическому (быстрому) или изотермическому (медленному).
Откроем сосуд, дадим части газа возможность покидать сосуд достаточно быстро (адиабатически) до выравнивания давления внутри
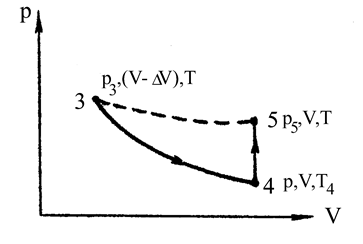 |
Рис.2. Адиабатическое расширение и
изохорическое нагревание газа в сосуде
V - объем сосуда; р - атмосферное давление; Т - температура газа вне сосуда (комнатная); DV- объем газа в состоянии 3 , который покидает сосуд в процессе (3®4); m/m - число молей газа, оставшегося в сосуде в результате процесса (3®4).
Для процесса (3®4)
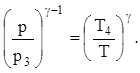 (11)
(11)
Для процесса (4®5)
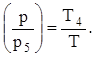 (12)
(12)
Подставляем (12) в (11), после логарифмирования имеем:
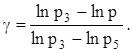 (13)
(13)
Для малых разностей давлений можно записать
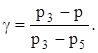 (14)
(14)
При измерении жидкостным манометром разностей
(р3 – р) = H, (p5 – p) = h,
![]() (15)
(15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.