Полиномиальный метод синтеза: стабилизация перевернутого маятника

 СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2012. – № 2(68). – 3–10

автоматическое управление
и идентификация

УДК 681.513

ПОЛИНОМИАЛЬНЫЙ МЕТОД СИНТЕЗА: СТАБИЛИЗАЦИЯ ПЕРЕВЕРНУТОГО МАЯТНИКА*

А.А. Воевода, Е.В.ШОБА

Приводится алгоритм расчёта регулятора для стабилизации положения перевёрнутого маятника. Помимо достижения вертикального положения маятника, так же ставится задача поддержания постоянной скорости движения платформы. Расчёт осуществляется полиномиальным методом в соответствии с разработанной методикой изложенной в диссертации Шобы Е.В. "Полиномиальный синтез многоканальных систем управления". Особенностью данной задачи является "неквадратный объект управления". Система включает ПИ регулятор и ПИД регулятор.

Ключевые слова: перевернутый маятник, тележка, модель объекта, ПИ и ПИД регуляторы, полиномиальный синтез, модальный синтез.

ВВЕДЕНИЕ

Интересным является не просто достижение нулевого отклонения маятника от положения равновесия, но и стабилизация системы по какому либо параметру, например расстоянию или скорости. В предыдущей работе [4] рассматривался расчёт регулятора для стабилизации угла отклонения и выхода на определённое расстояние или скорость. Расчёт проводился без использования матричного полиномиального представления. В данной работе делается попытка применить существующую методику синтеза регуляторов полиномиальным методом для многоканальных систем управления. При этом для решения задачи синтеза необходимо решить матричное характеристическое уравнение системы (диофантово уравнение).

1. ПОСТАНОВКА ЗАДАЧИ

Поставим задачу стабилизации положения маятника в вертикальном положении , во-первых, и во-вторых, достигнуть заданной скорости перемещения тележки. Синтез выполняем полиномиальным методом в соответствии с методикой, изложенной в [5-8].

Перевернутый маятник на тележке с силой , приложенной к тележке, можно рассматривать как "неквадратный" объект с одним входом и двумя выходами , где , - матрица-столбик размером , , - угловое положение маятника, - скорость перемещения тележки. Регулятор выбираем размером : . Передаточные функции объекта и числовые значения параметров возьмем из [3]:

, ,

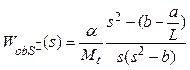где , , , , 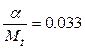.  Откуда

, .

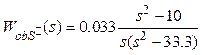Структурная схема системы представлена на Рис 1.

 

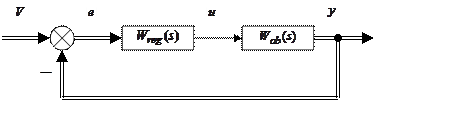Рис 1. Структурная схема системы

Здесь вектор задания имеет первую компоненту равную нулю - задаем положение маятника с нулевым отклонением от вертикали,  - задание на скорость. Задачу будем решать с использованием полиномиального представления объекта и регулятора. Придерживаемся методики, изложенной в [5-8]. Особенностью данной задачи является "не квадратность" объекта.

2. РЕШЕНИЕ ЗАДАЧИ

Найдем левое полиномиальное разложение объекта. Развернем

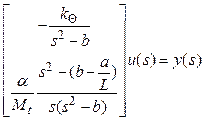
и умножим слева на такую диагональную матрицу, которая позволит избавиться от дробей:

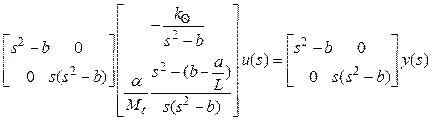
или

.

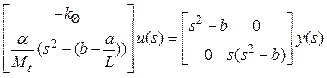Получили левое полиномиальное разложение объекта

,

где

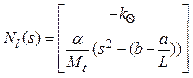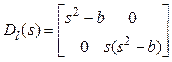, , или .

или в числах

, .

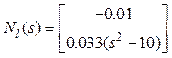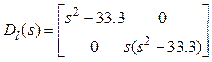Сформируем структуру объекта по заданным передаточным функциям. Введем передаточные функции, описывающие знаменатели объекта:

,.

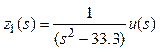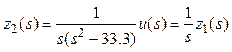Очевидно, что

,.

Теперь несложно получить структурную схему объекта Рис. 1.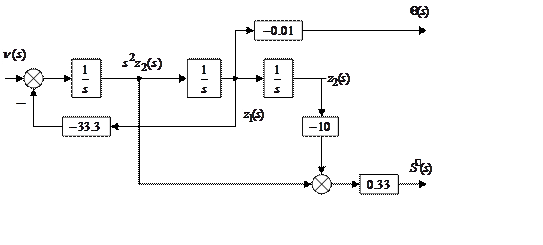

Рис. 1. Структурная схема объекта

Согласно методике синтеза необходимо найти правое полиномиальное разложение объекта, Кроме того, остается открытым вопрос о взаимной простоте левого полиномиального разложения объекта.

Найдем правое полиномиальное разложение объекта. Определим размеры матриц:

.

           

Составляем матрицу , которую необходимо операциями над столбцами привести к нижне треугольному виду. Перейдем к более привычным операциям над строками (приводить к верхне треугольному виду), для чего транспонируем матрицу :

.

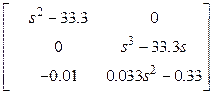
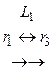
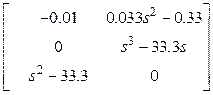
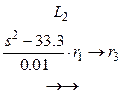
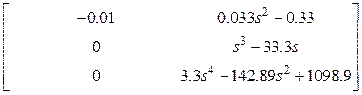
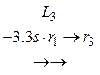
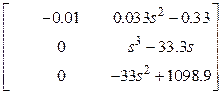
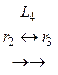
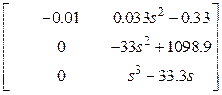
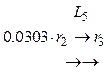
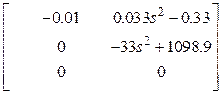Матрица вверху размером  это матрица  - наибольший общий правый делитель левого полиномиального разложения объекта . Она не унимодальная, следовательно, левое разложение не взаимно простое. Выпишем матрицы , выполняющие операции над строчками :

, , , , ,

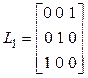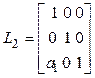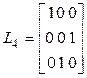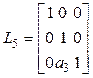где , , . Далее найдем произведение :

.

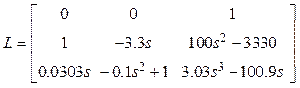Матрицу  можно представить как блочную матрицу

  .

                                                       

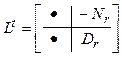
Получили правое полиномиальное разложение объекта:

.

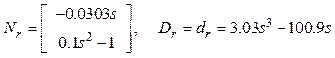Проверим правильность вычисления :

=

.

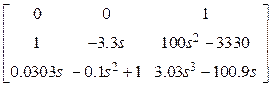
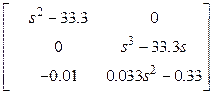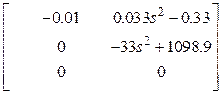Проверим правильность вычисления : из равенства

следует , которое и проверяем непосредственной подстановкой:

=.

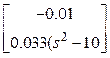
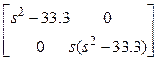
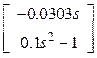Равенство справедливо.

Сформируем структуру правого полиномиального разложения объекта.

"Знаменатель" объекта - введем переменную ,

Откуда  и, далее, так как

, ,

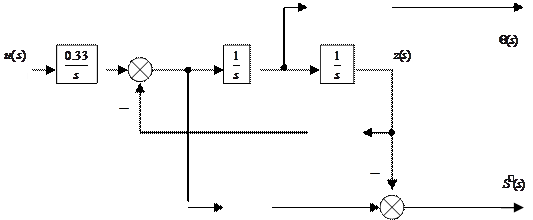
получаем структурную схему объекта Рис.2.

Рис.2. Структурная схема объекта

Формирование структурной схемы регулятора. Выберем регулятор в виде двух регуляторов: ПИД и ПИ, включенных параллельно, как показано на Рис. 3.

 

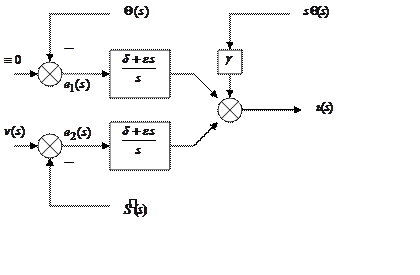Рис. 3. Два регулятора: ПИД и ПИ

Предполагается, что задание по углу отклонения маятника от вертикали тождественно равно нулю. Очевидно, что эта структура не минимальная - несложно найти минимальную структуру Рис 1.4.

 

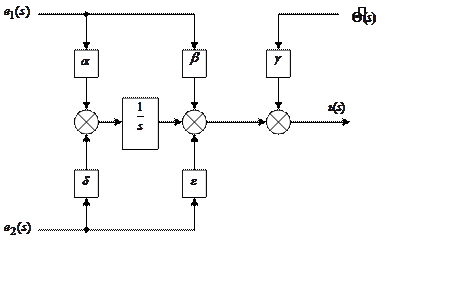Рис 1.4 Регулятор: два входа и один выход

Структурная схема системы приведена на Рис 1.5.

 

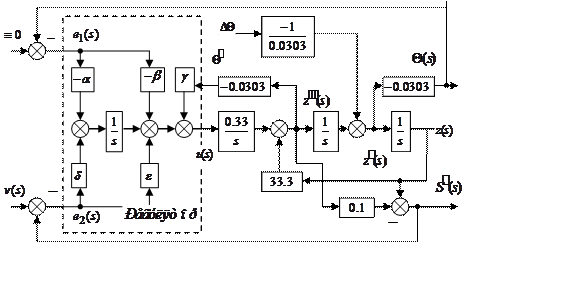Рис 1.5 Структурная схема системы

Очевидно, что

, ,.

(1)

Для единообразия обратные связи по выходному сигналу взяты отрицательными - из-за этого сменились знаки перед коэффициентами  и .

Расчет параметров регулятора.

Найдем передаточную функцию по каналу . Для этого опишем систему на Рис 1.5 уравнениями:

,

,

.

Первое и третье уравнения умножим на ,а второе на :

	(2)
,	(3)
.	(4)

Умножим (3) на  и вместо  подставим в (2):

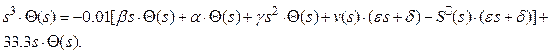
Полученную формулу умножим на  и вместо  подставим в (4):

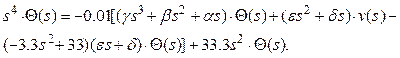
В результате перегруппировки получаем

Полином в левой части это характеристический полином системы. Зададим его равным . Приравнивая коэффициенты при одинаковых степенях, получим систему уравнений относительно неизвестных:

,

, .

Получили четыре уравнения с пятью неизвестными. Одно из неизвестных, например ,  можно задавать произвольно. Предыдущие уравнения запишем в матричном виде: