|
|
(5) |
Если
выбрать параметры регулятора в соответствии с (5),
передаточная функция по каналу ![]() будет равна
будет равна
![]() .
.
Пусть ![]() , тогда
, тогда ![]() , тогда
, тогда ![]()
![]() , тогда
, тогда ![]() .
.
|
|
(6) |
Найдем
передаточную функцию по каналу ![]() . Если из системы уравнений,
описывающих Рис 1.5 исключить
. Если из системы уравнений,
описывающих Рис 1.5 исключить
![]() и оставить
и оставить ![]() , получим
туже систему уравнений (5) для
определения параметров регулятора. При этом передаточная функция окажется
равной
, получим
туже систему уравнений (5) для
определения параметров регулятора. При этом передаточная функция окажется
равной
![]() .
.
Расчет через полиномиальные матрицы. Выпишем характеристическую полиномиальную матрицу для данной системы:
|
|
(7) |
Вспомним, что
![]() ,
, ![]() ,
, ![]() ,
, 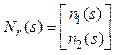
и подставим последние выражения в (7):
|
|
(8) |
Здесь
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Старший
член в (8) не нормирован - для нормировки разделим "числитель" и "знаменатель"
объекта на коэффициент 3.03:
. Старший
член в (8) не нормирован - для нормировки разделим "числитель" и "знаменатель"
объекта на коэффициент 3.03:
![]() ,
, ![]() ,
, ![]() .
.
В общем виде это запишется так:
![]() ,
, ![]() ,
, ![]() .
.
В
формуле (8) знак минус перед ![]() стоит в соответствии с Рис 1.5 - формула
(8)
предполагает отрицательную обратную связь как по каналам
стоит в соответствии с Рис 1.5 - формула
(8)
предполагает отрицательную обратную связь как по каналам ![]() ,
, ![]() так и
по каналу
так и
по каналу ![]() . Развернем (8)
. Развернем (8)
![]()
и приравняем коэффициенты при равных степенях:
![]() ,
, ![]()
![]() ,
, ![]() .
.
Запишем в матричном виде
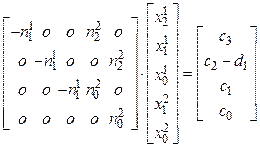 .
.
Получили четыре уравнения с пятью неизвестными - одно из неизвестных перенесем в правую часть (его можно задавать произвольно):
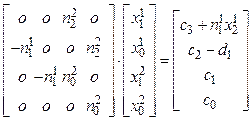 .
.
При заданных значениях параметров объекта управления получим
|
|
(9) |
Параметры регулятора соответствуют (6).
Моделирование системы.
Интересными
представляются результаты моделирования поведения системы. Напомним, что
система стремится стабилизировать вертикальное положение маятника и при этом происходит
поддержание заданной скорости движения тележки. Передаточные функции, описывающие
связь по каналу ![]() и каналу
и каналу ![]() получены
выше и имеют следующий вид:
получены
выше и имеют следующий вид:
![]() ,
, ![]()
Параметры регулятора
соответствуют (6). ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
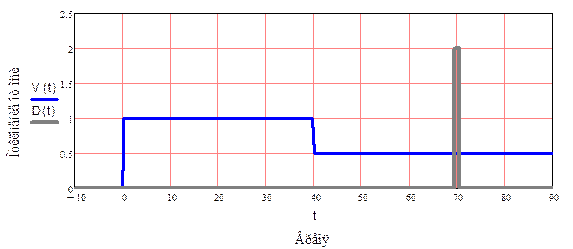
В качестве тестового сигнала будет формировать задание скорости: В начальный момент скорость задаём равную условной единице. Через время равное 40 сек. Задаём новое значение скорости равное 0.5. Через время 70 с. имитируем "толчок".
Примечание. Интересно задавать следующее значение
скорости, меньше предыдущего, что эквивалентно воздействию на маятник внешней
тормозящей силы. В этом случае отклонение угла ![]() происходит
в противоположную сторону, затем произойдёт выход на заданную меньшую скорость.
Если же задавать следующее значение скорости больше предыдущего, то это эквивалентно
приложению внешней ускоряющей силы. В этом случае отклонение угла
происходит
в противоположную сторону, затем произойдёт выход на заданную меньшую скорость.
Если же задавать следующее значение скорости больше предыдущего, то это эквивалентно
приложению внешней ускоряющей силы. В этом случае отклонение угла ![]() происходит в первоначальную сторону, затем
произойдёт выход на заданную большую скорость.
происходит в первоначальную сторону, затем
произойдёт выход на заданную большую скорость.
 В случае имитации "толчка"
прикладывается импульс ограниченной длительности к тележке, в связи с чем
происходит изменение угла и скорости движения. Через некоторое время происходит
стабилизация данных параметров.
В случае имитации "толчка"
прикладывается импульс ограниченной длительности к тележке, в связи с чем
происходит изменение угла и скорости движения. Через некоторое время происходит
стабилизация данных параметров.
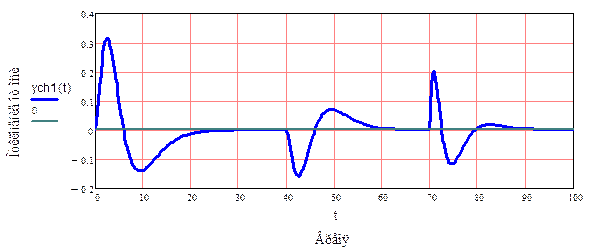 Рис. 6. Внешние
воздействия на систему
Рис. 6. Внешние
воздействия на систему
Рис.7. Отклонение
угла ![]()
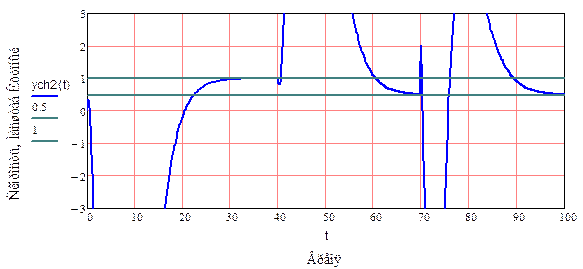
Рис. 8. Отклонение скорости (крупный масштаб)
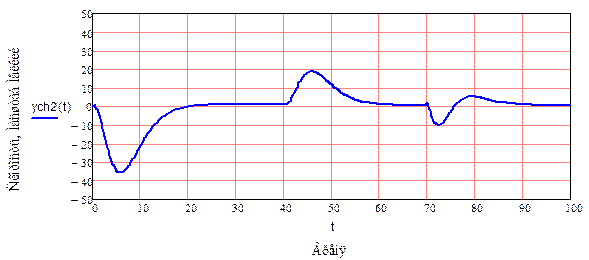
Рис.9. Отклонение скорости (мелкий масштаб)
Рис. 6 показывает характер воздействий на систему. Рис.7 показывает изменение угла отклонения от верткальной оси. Графики Рис. 8 и Рис.9 показывают изменения скорости в разных масштабах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.