СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2012. – № 1(__). – 3–10
автоматическое управление
и идентификация
УДК 681.513
УПРАВЛЕНИЕ ПЕРЕВЕРНУТЫМ МАЯТНИКОМ*
А.А. Воевода, Е.В.ШОБА
Приведены линеаризованные модели перевернутого маятника на тележке, соответствующие случаю, когда пренебрегаем моментом инерции маятника. У объекта один вход и два выхода. Рассмотрены несколько вариантов стабилизации положения маятника на основе модального метода с использованием полиномиальных представлений.
Ключевые слова: перевернутый маятник, тележка, модель объекта, стабилизация положения маятника, модальный метод синтеза, полиномиальное представление.
Перевернутый маятник на тележке представляет собой хороший тестовый пример для апробации различных методов синтеза [1, 2]. В данной работе используем числовые значения, приведенные в [3], а именно, моментом инерции маятника пренебрегаем. Специфика этого объекта заключается в том, что число входов не равно числу выходов, а именно управляющий сигнал один, а регулируемых величин две. Уточним задачу – потребуем стабилизации положения маятника в верхнем положении и будем управлять положением тележки или ее скоростью. Ограничимся простейшими законами управления.
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим перевернутый маятник на тележке (Рис.1): ![]() - масса тележки,
- масса тележки, ![]() -
масса маятника,
-
масса маятника, ![]() - координата центра тяжести
тележки (по горизонтальной оси - расстояние от центра тяжести,
- координата центра тяжести
тележки (по горизонтальной оси - расстояние от центра тяжести, ![]() - координата центра тяжести маятника (по
горизонтальной оси),
- координата центра тяжести маятника (по
горизонтальной оси), ![]() - отклонение маятника от вертикали,
- отклонение маятника от вертикали,
![]() - сила, приложенная к тележке,
- сила, приложенная к тележке, ![]() ,
, ![]() - силы,
вызванные воздействием маятника на тележку (Рис.1б) и воздействием тележки на
маятник (Рис.1в),
- силы,
вызванные воздействием маятника на тележку (Рис.1б) и воздействием тележки на
маятник (Рис.1в), ![]() - реакция опоры на тележку,
- реакция опоры на тележку, ![]() - вес маятника,
- вес маятника, ![]() - момент
инерции маятника относительно центра тяжести. Ниже использованы обозначения
- момент
инерции маятника относительно центра тяжести. Ниже использованы обозначения
![]() ,
, ![]() .
.
1.1. Линеаризованная модель [3].
Рассмотрим модель перевернутого маятника на тележке для случая когда
![]() ,
, ![]() . Линеаризация осуществлена в окрестности точки
. Линеаризация осуществлена в окрестности точки
![]() и
и ![]() :
:
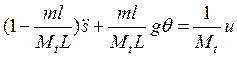 . (1)
. (1)
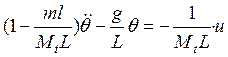 . (2)
. (2)
Обозначим
через 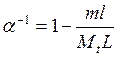 . Тогда (1), (2) преобразуются в
. Тогда (1), (2) преобразуются в
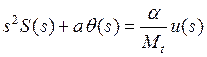 ,
, 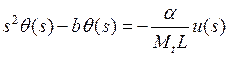 .
(3а, 3б)
.
(3а, 3б)
где
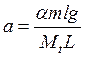 ,
, 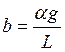 .
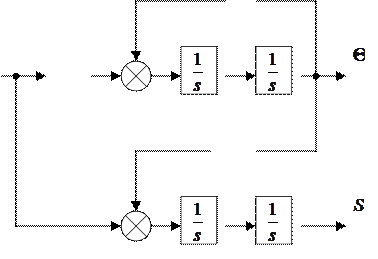
Структурная схема, соответствующая (3), приведена на рис.1.
.
Структурная схема, соответствующая (3), приведена на рис.1.
 |
|||||
|
|||||
|
|
|
|
Рис.1. Структурная схема объекта
Приведем передаточные функции по двум каналам:
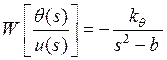 ,
, 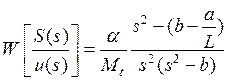 , (4а,
4б)
, (4а,
4б)
где
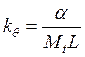 . Первая передаточная функция легко
получается из (3б), а для вывода (4б) из (3б) находим
. Первая передаточная функция легко
получается из (3б), а для вывода (4б) из (3б) находим 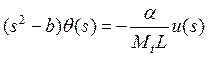 и
подставим в преобразованную формулу (3а):
и
подставим в преобразованную формулу (3а):
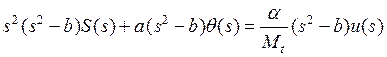 .
.
Откуда получаем
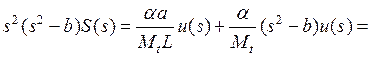
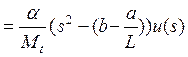 .
.
Уточним параметры передаточных функций для случая, когда ![]() :
:
![]() ,
, 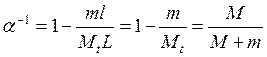 ,
,
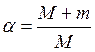 ,
, 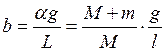 ,
,
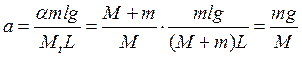 .
.
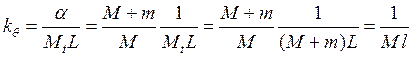 ,
,
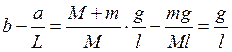
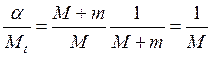
Зададим параметры объекта для случая, когда ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда
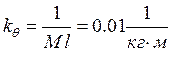 ,
, 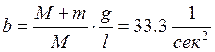 ,
,
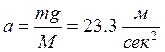 ,
, 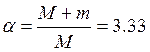 ,
,
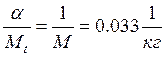 ,
, 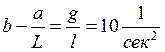 .
.
Перепишем передаточные функции (4) при заданных значениях параметров:
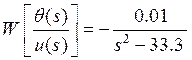 ,
, 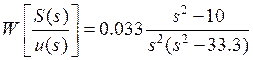 . (5а,
5б)
. (5а,
5б)
2. СИНТЕЗ РЕГУЛЯТОРОВ
2.1. Задача первая. Поставим задачу стабилизации положения маятника в
вертикальном положении (![]() ) во – первых, и во –
вторых, переместить тележку в заданное положение
) во – первых, и во –
вторых, переместить тележку в заданное положение ![]() [см
англ - прототип]. При этом предполагаем доступность для измерения
[см
англ - прототип]. При этом предполагаем доступность для измерения ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Один
из вариантов решения задачи – взять регулятор, например, ПИД – регулятор в цепи
обратной связи, и построить систему “ПИД – регулятор - объект
. Один
из вариантов решения задачи – взять регулятор, например, ПИД – регулятор в цепи
обратной связи, и построить систему “ПИД – регулятор - объект ![]() ”, которая обеспечивает вертикальное
положение маятника. Для управления положением используем также ПИД – регулятор
но разместим его в прямой цепи. Для форсирования процессов по возмущению
дифференциальную часть поставим в цепи обратной связи. Структурная схема
системы приведена на рис.2.
”, которая обеспечивает вертикальное
положение маятника. Для управления положением используем также ПИД – регулятор
но разместим его в прямой цепи. Для форсирования процессов по возмущению
дифференциальную часть поставим в цепи обратной связи. Структурная схема
системы приведена на рис.2.
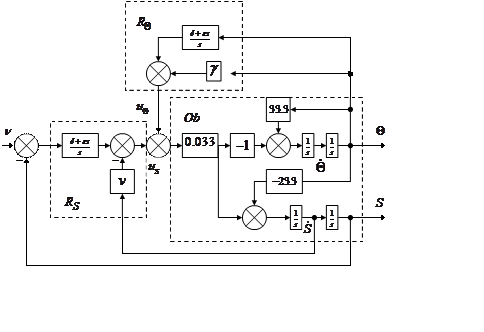
Рис.2. Структурная схема системы “объект + два ПИД – регулятора”
Примечание 1. Если бы стояла отдельная задача стабилизации положения маятника с
использованием одного ПИД – регулятора в цепи обратной связи, задача
существенно бы упростилась: из рис.2 следует отбросить регулятор ![]() и два интегратора из объекта,
соответствующих каналу по S. Опишем
систему уравнениями
и два интегратора из объекта,
соответствующих каналу по S. Опишем
систему уравнениями
![]() ,
(6а)
,
(6а)
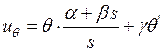 ,
(6б)
,
(6б)
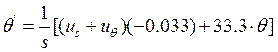 . (6в)
. (6в)
Здесь ![]() можно трактовать как
задание на положение маятника по углу
можно трактовать как
задание на положение маятника по углу ![]() ,
, ![]() - выход регулятора
- выход регулятора ![]() ,
,
![]() - не производная, а переменная на выходе
первого интегратора объекта (совпало с обозначением производной). Подставим
- не производная, а переменная на выходе
первого интегратора объекта (совпало с обозначением производной). Подставим ![]() из (6а) в (6б) и (6в) и, далее, (6б) в
(6в):
из (6а) в (6б) и (6в) и, далее, (6б) в
(6в):
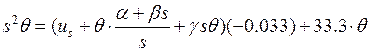 .
.
После несложных преобразований получим
![]()
Допустим, желаемый характеристический полином такой
усеченной системы будет задан вида ![]() , что обеспечивает
переходный процесс порядка 0.5 С. Приравнивая коэффициенты двух последних
выражений, получим систему уравнений:
, что обеспечивает
переходный процесс порядка 0.5 С. Приравнивая коэффициенты двух последних
выражений, получим систему уравнений:
![]() ,
, ![]() ,
, ![]() ,
,
откуда находим параметры регулятора
![]() ,
, ![]() ,
, ![]() .
.![]()
Найдем передаточную функцию системы рис.2 по каналу “V-S”, для чего опишем ее уравнениями:
![]() ,
, ![]() (7а,
7б)
(7а,
7б)
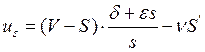 ,
, 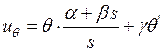 , (7в, 7г)
, (7в, 7г)
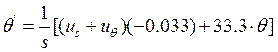 ,
(7д)
,
(7д)
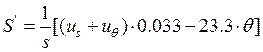 .
(7е))
.
(7е))
Исключим
переменные ![]() и
и ![]() из
системы (7), для чего подставим (7а) и (7б) в остальные уравнения:
из
системы (7), для чего подставим (7а) и (7б) в остальные уравнения:
![]() ,
, ![]() (8а),
(8б)
(8а),
(8б)
![]() , (8в)
, (8в)
![]() . (8г)
. (8г)
Описание системы сократилось до четырех уравнений (8а) – (8г). Сложим (8а) и (8б)
![]()
и
подставим в (8г), предварительно умноженное на ![]() :
:
![]() .
.
Перегруппируем
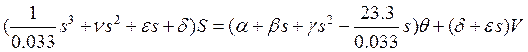
и
умножим на ![]() :
:
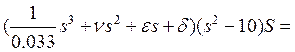
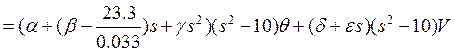 . (9)
. (9)
Осталось
исключить из (9) переменную ![]() - если сложить (8в) и
(8г), получим
- если сложить (8в) и
(8г), получим
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.