Управление перевернутым маятником, страница 2

Воспользуемся последним соотношением для исключения  из (9):

    .

Осталось перегруппировать члены по степеням s

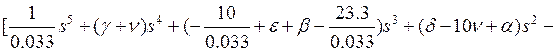
и избавиться от множителя 0.033:

                 (10)

В левой части получили характеристический полином системы, представленной на рис.2. Зададим желаемый характеристический полином вида

,                       (11)

корни которого {-5, -5, -5, -1, -1}.

Примечание 2. Желательно было бы задать корни контура стабилизации угла равными {-5, -5, -5}, а контура управления положением равными {-1, -1}. Этим обеспечили бы более быструю реакцию системы на компенсацию отклонения маятника от вертикального положения. Следует обратить внимание на то, что система на рис.2 имеет шесть интеграторов, в то время как порядок характеристического полинома системы равен пяти. Это говорит о том, что структура на рис.2 не минимальная.

Приравнивая коэффициенты характеристического полинома системы (10) и желаемого полинома (11), получим систему уравнений

,  ,

,  ,  ,

которые легко упрощаются:

, , ,

, .

Из второго уравнения находим . Осталось два уравнения

,

с тремя неизвестными. Возьмем, следуя примечанию 2 и, далее, примечанию 1, . Получили следующие значения параметров регуляторов для корней замкнутой системы{-5, -5, -5, -1, -1}:

, , ,

, , .

Если замедлить процессы в системе и задать корни {-5, -5, -5, -0.5, -0.5}, что соответствует полиному

,         (12)

Получим систему уравнений

,  ,

,  ,  ,

из которой, полагая , определим параметры регулятора

, , ,

, , ,

что соответствует корням системы {-5, -5, -5, -0.5, -0.5}.

Моделирование системы. При подаче на вход V единичного сигнала система переходит  в положение S=1 за, примерно, 8 секунд с перерегулированием 20% и при этом во время переходного процесса отклонение по углу не превышает 0.1 рад. При подаче возмущения  переходный процесс продолжается не более 2 сек  с быстрой компенсацией отклонения и выбросом в противоположную сторону не более 0.2 рад. При подаче линейно нарастающего сигнала по V система отрабатывает сигнал без ошибки. Недостатком такой системы является перерегулирование по S  порядка 20%. Для ограничения сигналов на выходах регуляторов Следует сформировать задающий сигнал типа двойной экспоненты, тогда перерегулирование будет не более 10%.

2.2. Задача вторая. Естественно изменить задачу – а именно - построить управление не по , а по  - по скорости перемещения тележки, а регулятор взять ПИ. Структурная схема соответствует рис.2 без интегратора в цепи  и приведена на рис.3.

Найдем передаточную функцию системы рис.3 по каналу , для чего опишем ее уравнениями:

                                         (13а)

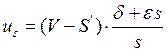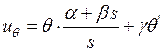, ,        (13б,13в)

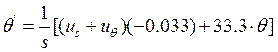,                        (13г)

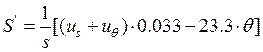.                           (13д))

Исключим переменную  из системы (13), для чего подставим (13а) в остальные уравнения:

,       (14а), (14б)

,                             (14в)

.                               (14г)

Описание системы сократилось до четырех уравнений (14а) – (14г). Сложим (14а) и (14б)

и подставим в (14г), предварительно умноженное на :

.

Перегруппируем

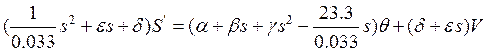
и умножим на :

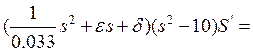
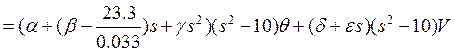.     (15)

Осталось исключить из (15) переменную  - если сложить (14в) и (14г), получим

.

Воспользуемся последним соотношением для исключения  из (15):

    .

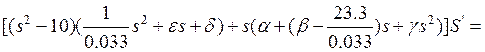
Осталось перегруппировать члены по степеням s

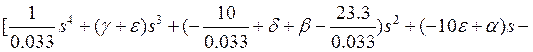
и избавиться от множителя 0.033:

                 (16)

В левой части получили характеристический полином системы, представленной на рис.3. Зададим желаемый характеристический полином вида

,                       (17)

корни которого равны {-5, -5, -5, -1}.

Приравнивая коэффициенты характеристического полинома системы (16) и желаемого полинома (17), получим систему уравнений

,  ,

,  ,

которые легко упрощаются: 

, , , .

Из второго уравнения находим . Осталось два уравнения

,

с тремя неизвестными ,  и . Возьмем, следуя примечанию 2 и, далее, примечанию 1, . Получили следующие значения параметров регуляторов для корней замкнутой системы{-5, -5, -5, -1}:

, , , , .

2.3. Задача третья. Представить объектуправления как объект, имеющий один вход и три выхода , ,  и решить задачу стабилизации . В данной статье эта задача рассматриваться не будет.

ЗАКЛЮЧЕНИЕ

Продемонстрирована методика синтеза положением “неквадратного” объекта с использованием модального метода синтеза. В предположении доступности вектора состояния оказалось возможным использовать простейшие законы управлении – ПИД и ПИ регуляторы.

[1] M.Dahleh, M.A.Dahleh, G.Verghese. Lectures on dynamic systems and control. 2003. Massachuasetts Institut of technology. 600 p.

[2] J.Doyle, B.Francis, A.Tannenbaum. Feedback control theory. Macmillan Publishing. 1990. 198 p.

[3] Воевода А.А., Шоба Е.В. О модели перевёрнутого маятника: Сб. науч. тр. - НГТУ: Изд-во НГТУ, 2012. - №1(67). - c. 3-14.

Воевода Александр Александрович - профессор кафедры автоматики Новосибирского государственного технического университета. 

e-mail: ucit@ucit.ru.

Шоба  Евгений Владимирович - соискатель кафедры автоматики Новосибирского государственного технического университета.

E-mail: nsk_nstu@mail.ru.

A.A. Voevoda,  E.V. Shoba. ABOUT MODEL INVERTED PENDULUM.

The nonlinear and linearized models of the inverted pendulum are given in the cart, corresponding to various cases, namely, at zero mass of the cart with the account and without the moment of inertia of a pendulum. Two block diagrams of the model one of which includes so-called “an algebraic ring” are analysed.

Keywords: the inverted pendulum, the cart, object model.