Методы гармонической линеаризации нелинейностей и методы расчета параметров автоколебаний в нелинейных системах

министерство образования РФ

Новосибирский Государственный Технический Университет

Кафедра Автоматики

Лабораторная работа №4

Метод гармонического баланса

НОВОСИБИРСК, 2007

Цель работы:

Ознакомиться с методами гармонической линеаризации нелинейностей и методами расчета параметров автоколебаний в нелинейных системах.

Исходные данные:

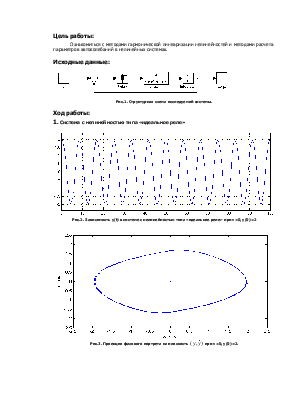
Рис.1. Структурная схема исследуемой системы.

Ход работы:

1. Система с нелинейностью типа «идеальное реле»

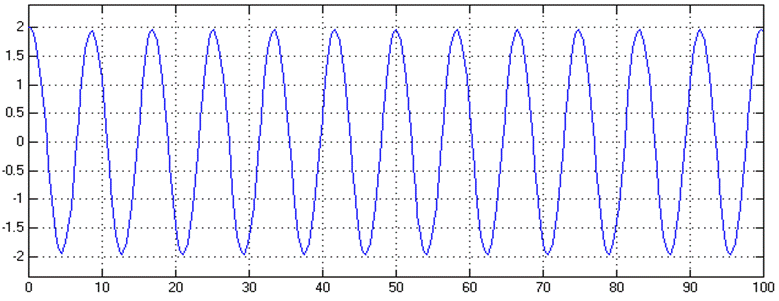
Рис.2. Зависимость y(t) в системе с нелинейностью типа «идеальное реле» при v=0, y(0)=2

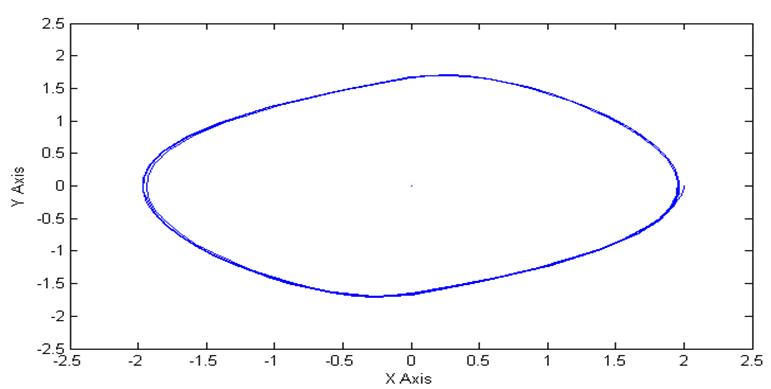
Рис.3. Проекция фазового портрета на плоскость  при v=0, y(0)=2.

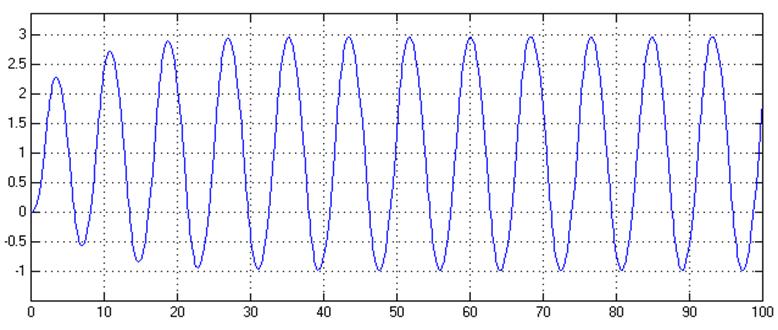
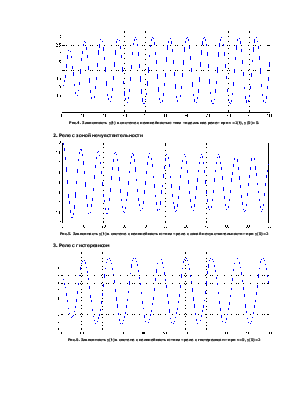
Рис.4. Зависимость y(t) в системе с нелинейностью типа «идеальное реле» при v=1(t), y(0)=0.

2. Реле с зоной нечувствительности

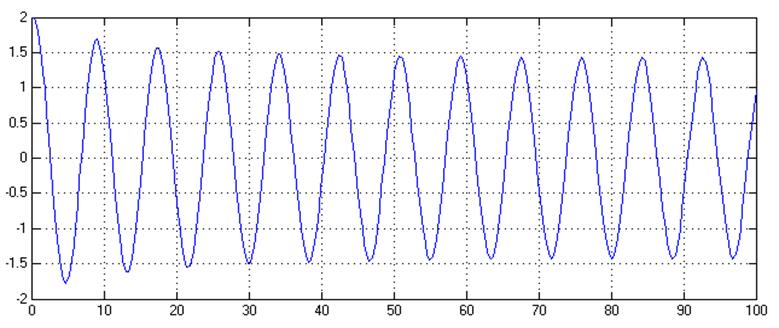
Рис.5. Зависимость y(t) в системе с нелинейностью типа «реле с зоной нечувствительности» при y(0)=2

3. Реле с гистерезисом

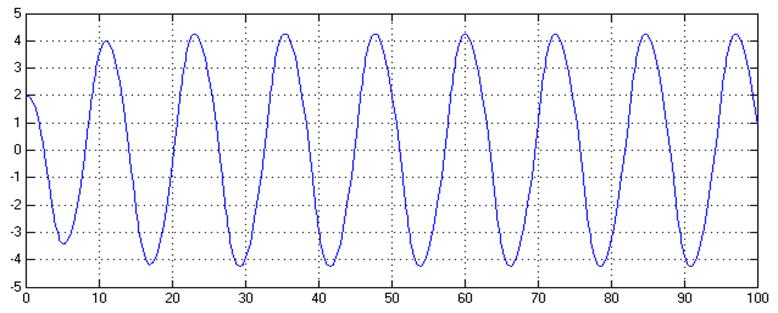
Рис.6. Зависимость y(t) в системе с нелинейностью типа «реле с гистерезисом» при v=0, y(0)=2

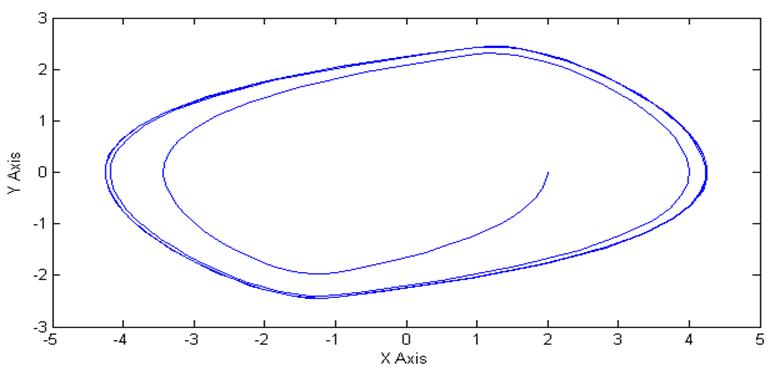
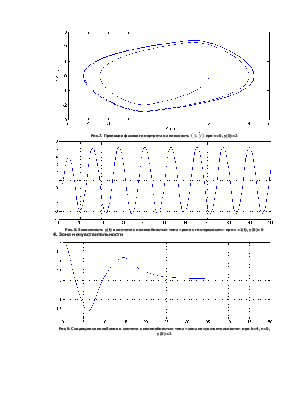
Рис.7. Проекция фазового портрета на плоскость  при v=0, y(0)=2

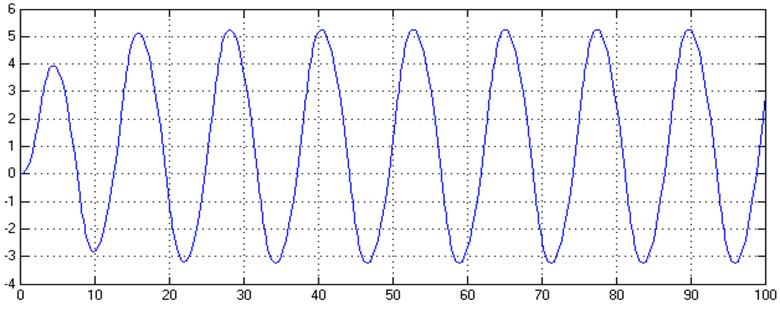
Рис.8. Зависимость y(t) в системе с нелинейностью типа «реле с гистерезисом» при v=1(t), y(0)=0

4. Зона нечувствительности

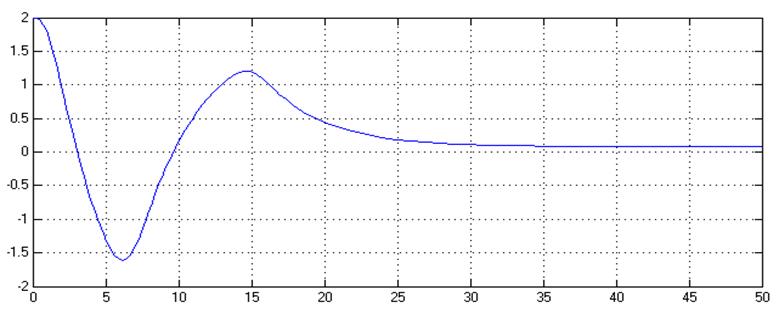
Рис.9. Сходящиеся колебания в системе с нелинейностью типа «зона нечувствительности» при k=4, v=0, y(0)=2

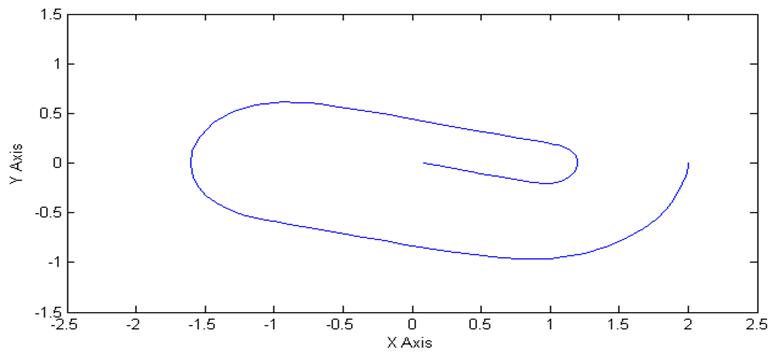
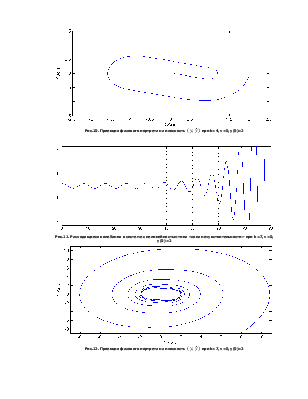
Рис.10. Проекция фазового портрета на плоскость  при k=4, v=0, y(0)=2

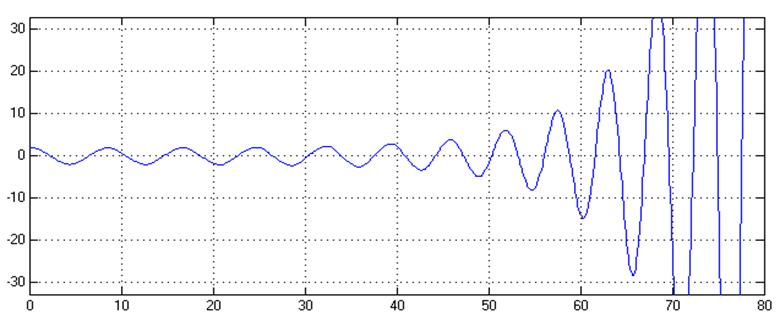
Рис.11. Расходящиеся колебания в системе с нелинейностью типа «зона нечувствительности» при k=7, v=0, y(0)=2

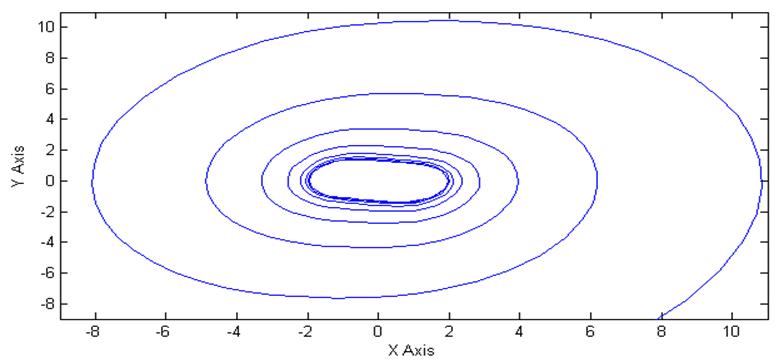
Рис.12. Проекция фазового портрета на плоскость  при k=7, v=0, y(0)=2

Выводы

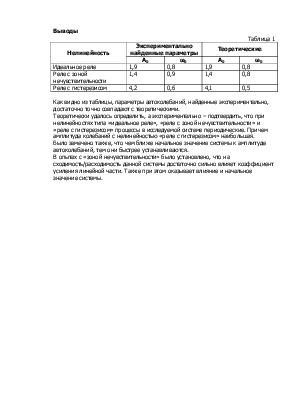
Таблица 1

Как видно из таблицы, параметры автоколебаний, найденные экспериментально, достаточно точно совпадают с теоретическими.

Теоретически удалось определить, а экспериментально – подтвердить, что при нелинейностях типа «идеальное реле», «реле с зоной нечувствительности» и «реле с гистерезисом» процессы в исследуемой системе периодические. Причем амплитуда колебаний с нелинейностью «реле с гистерезисом» наибольшая.

Было замечено также, что чем ближе начальное значение системы к амплитуде автоколебаний, тем они быстрее устанавливаются.

В опытах с «зоной нечувствительности» было установлено, что на сходимость/расходимость данной системы достаточно сильно влияет коэффициент усиления линейной части. Также при этом оказывает влияние и начальное значение системы.
Расчеты

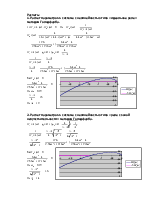
1. Расчет параметров в системе с нелинейностью типа «идеальное реле» методом Гольдфарба.

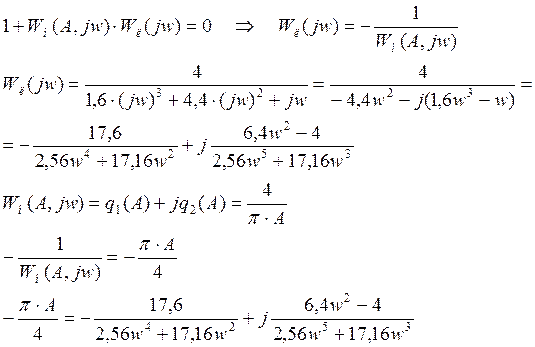
2. Расчет параметров в системе с нелинейностью типа «реле с зоной нечувствительности» методом Гольдфарба.

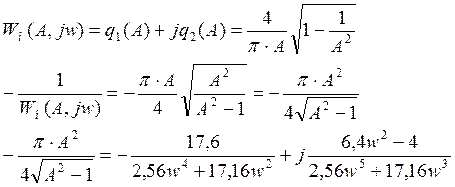
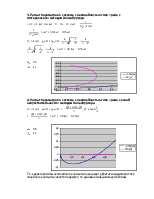
3. Расчет параметров в системе с нелинейностью типа «реле с гистерезисом» методом Коченбургера.

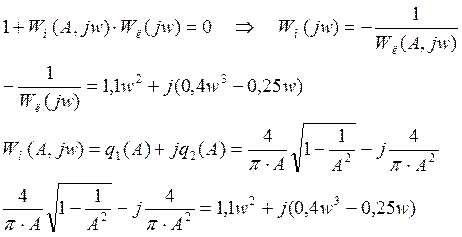
4. Расчет параметров в системе с нелинейностью типа «реле с зоной нечувствительности» методом Коченбургера.

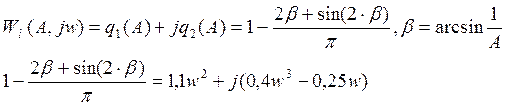
Т.к. характеристика нелинейного элемента пересекает обратную характеристику линейного элемента «изнутри наружу», то данные колебания неустойчивы.