Министерство образования и науки РФ
Федеральное агентство по образованию
НГТУ
Кафедра «Автоматики»
Лабораторная работа №10
АНАЛИЗ СВОЙСТВ СИСТЕМЫ С РАЗНОТЕМПОВЫМИ ДВИЖЕНИЯМИ
Группа: АА-324 Преподаватель:
Студенты: Заремба В.В. Шпилевая О.Я.
Семенцов А.B.
Новосибирск, 2006
Исследовать возможность разделения движений в системе при наличии малых инерционностей и оценить влияние различных параметров, как на полное движение, так и на отдельные его составляющие.
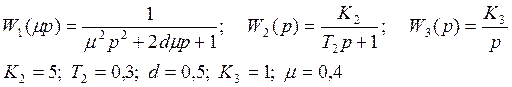
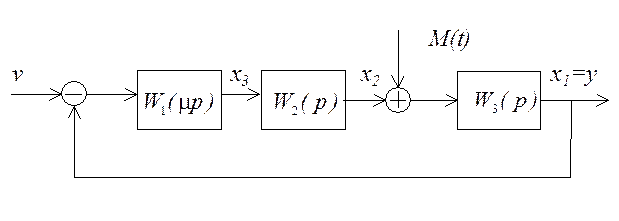
Ход работы:
Определение значения ![]() , при
котором разделение движений справедливо.
, при
котором разделение движений справедливо.
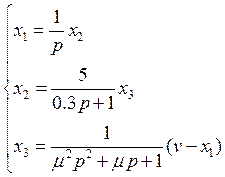
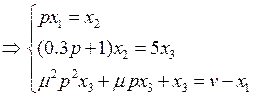
проведем замену переменной: ![]() .
.
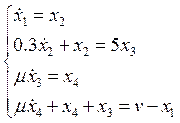
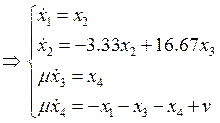
Считая ![]() , получим подсистему
медленных движений системы:
, получим подсистему
медленных движений системы:
ПМД
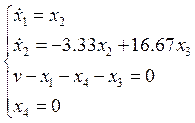
Упростим:
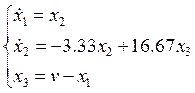
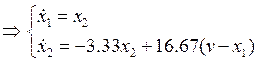
![]()
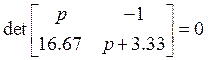
![]()
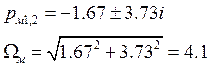
ПБД:
Перейдем к новой переменной времени:
![]() ,
, ![]() ,
следовательно
,
следовательно 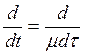
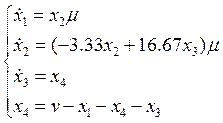
Считая ![]() , получим:
, получим:
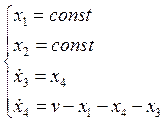
Вернемся к старому времени:
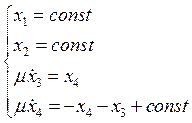
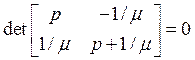
![]()
Найдем корни характеристического уравнения:
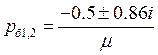
![]()
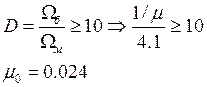
1.
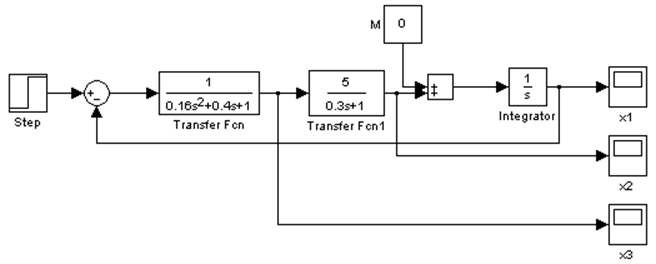
Рис.1.1. Структурная схема исследуемой системы.
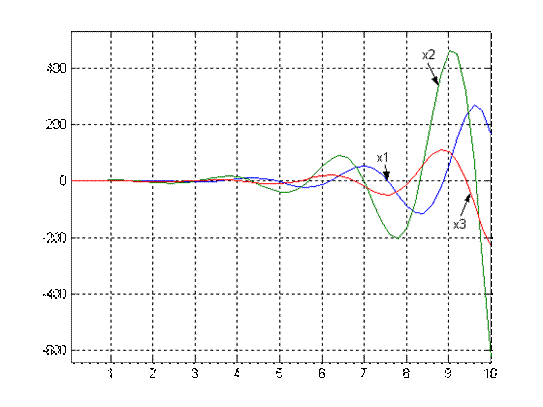
Рис.1.2. График переходного процесса x1(t), x2(t), x3(t) при V=1 и M(t)=0.
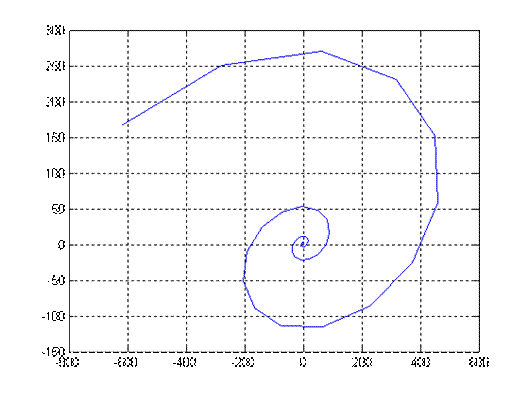
Рис.1.3. Проекция фазового портрета (x1,x2) на плоскость.
2.
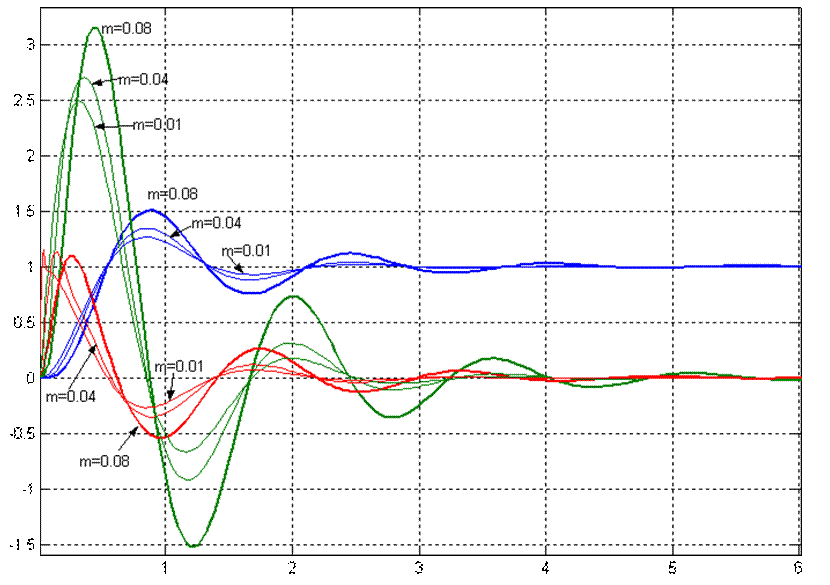
Рис.2.1. Переходные процессы x1(t)-синий, x2(t)-зеленый и x3(t)-красный при μ=0,08, μ=0,04, μ=0,01
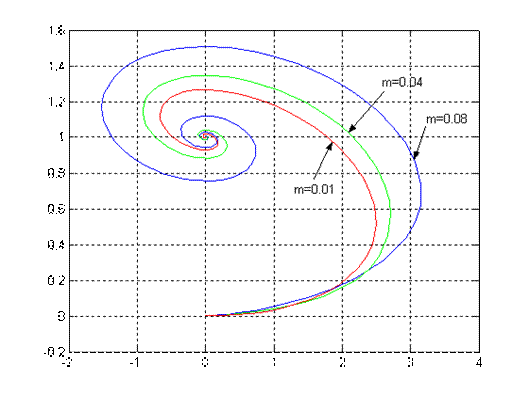
Рис.2.2. Проекция фазового портрета системы (x1,x2) при различных μ
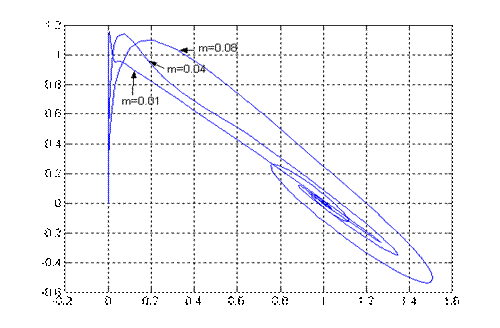
Рис.2.3. Проекция фазового портрета системы (x1,x3) при различных μ
 3.
3.
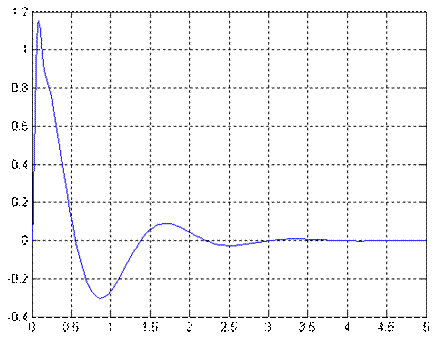
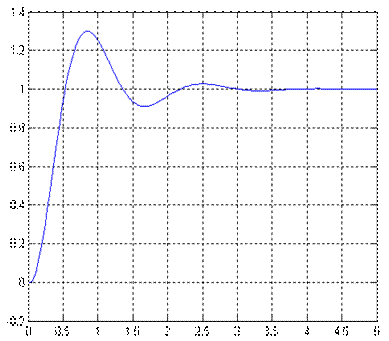
Рис.3.1. Переходный процесс x1(t) при Рис.3.2. Переходный процесс x3(t) при
рассчитанном значении μ=μ0 рассчитанном значении μ=μ0
σ=30%, tп=1,95 tп=1,97
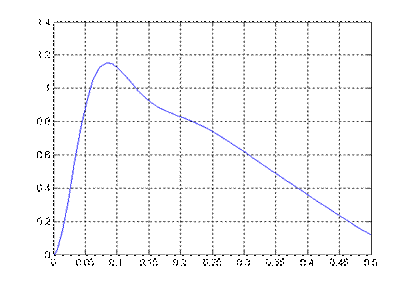
Рис.3.2. Переходный процесс x3(t) при рассчитанном значении μ=μ0 (время моделирования 0,5), tп=0,35
 4.
4.
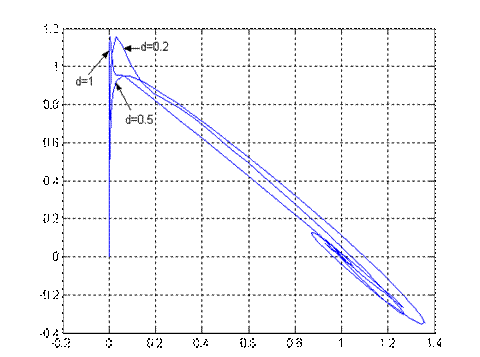
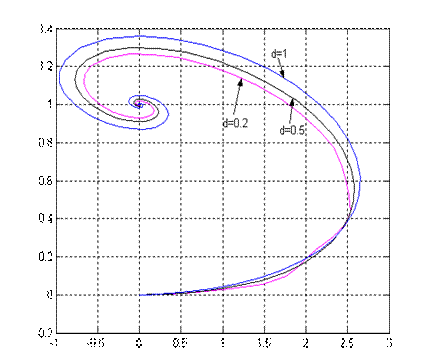
Рис.4.1. Проекция фазового портрета системы (x1,x2) и (x1,x3) при различных d
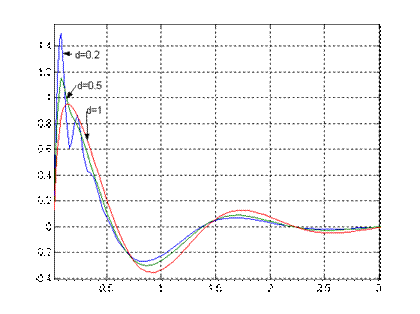
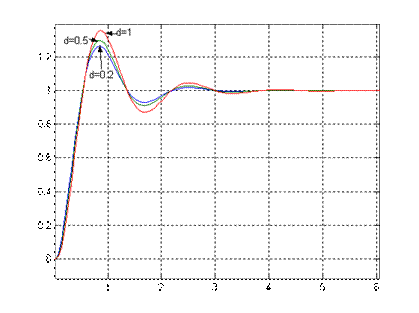
Рис.4.2. Переходный процесс x1(t) при Рис.4.3. Переходный процесс x3(t) при
различных значениях d различных значениях d
 5.
5.
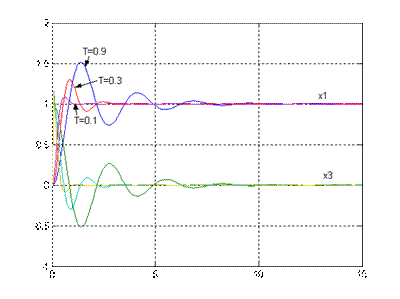
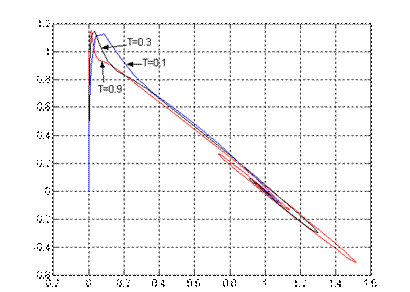
Рис.5.1. Переходный процесс x1(t), x3(t) при Рис.5.2. Проекция фазового портрета системы
различных значениях Т (x1,x3) при различных Т
 6.
6.
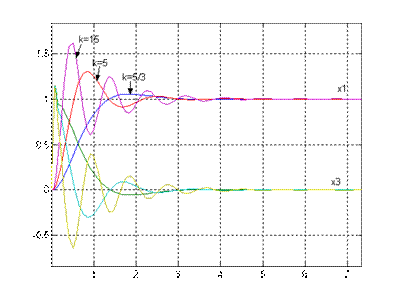
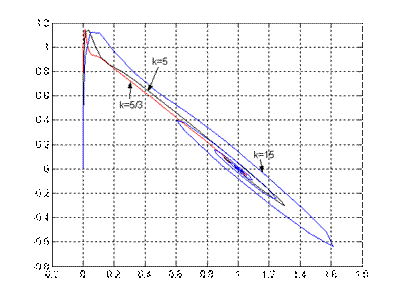
Рис.6.1. Переходный процесс x1(t), x3(t) при Рис.6.2. Проекция фазового портрета системы
различных значениях k (x1,x3) при различных k
 7.
7.
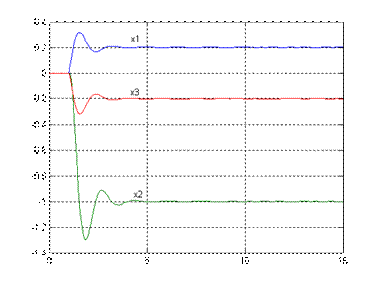
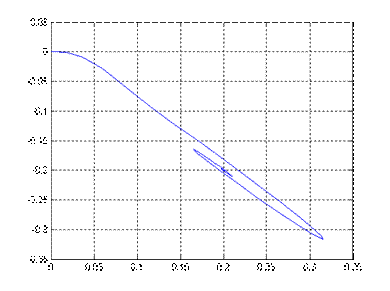
Рис.7.1. Проекция фазового портрета и переходные процессы
для переменных x1(t), x2(t) и x3(t) при ![]() , v=0
и M(t-t)=1, здесь t=1с - время возникновения
возмущающего воздействия
, v=0
и M(t-t)=1, здесь t=1с - время возникновения
возмущающего воздействия
8.
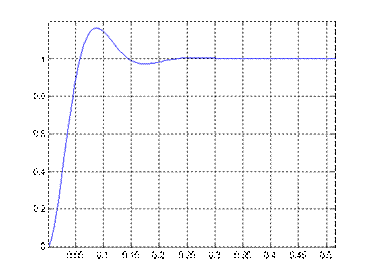
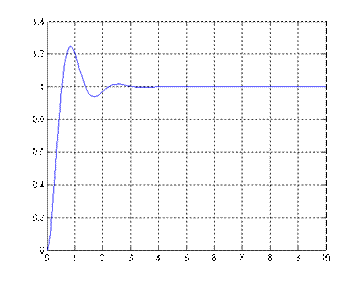
Рис.8.1. Переходный процесс ПМД Рис.8.2. Переходный процесс ПБД
σ=25%, tп=1,86 σ=16%, tп=0,13
9. Замена колебательного звена на входе системы апериодическим с передаточной функцией
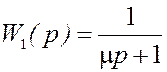
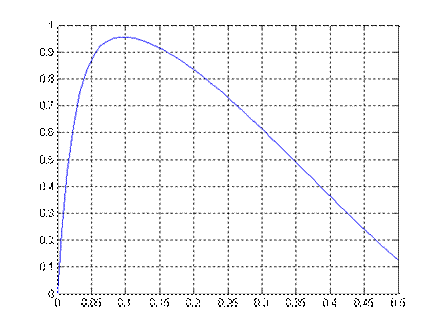
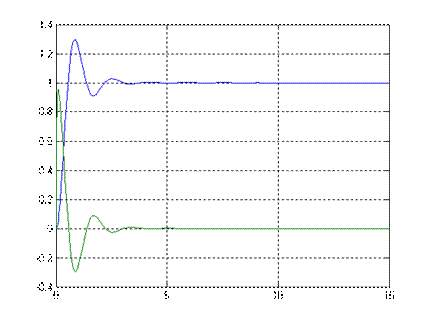
Рис.9.1. Переходный процесс x1(t), x3(t) Рис.9.2. Переходный процесс x3(t)
x1(t): σ=29%, tп=1,95; x3(t): tп=2 (время моделирования 0,5)
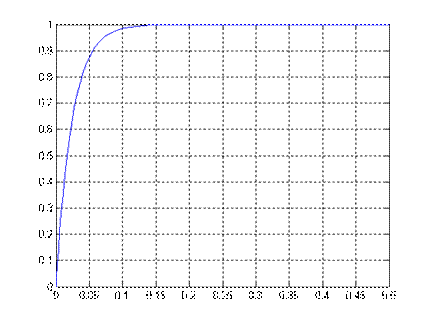
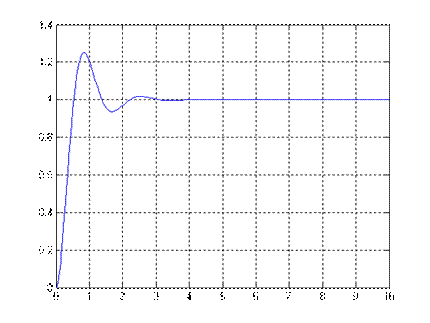
Рис.9.3. Переходный процесс ПМД Рис.9.4. Переходный процесс ПБД
σ=25%, tп=1,86 σ=0%, tп=0,07
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.