Анализ системы с разнотемповыми движениями.
1. Цель работы.
Исследовать возможность разделения движений в системе при наличии малых инерционностей и оценить влияние различных параметров как на полное движение, так и на отдельные его составляющие.
2. Модель исследуемой системы
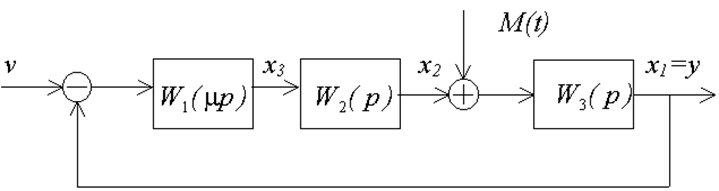
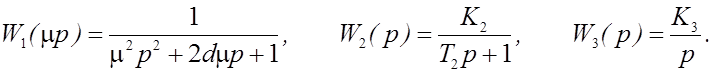
3. Вариант задания (исходные данные) [Вариант 5]
|
K2 |
T2 |
d |
K3 |
|
|
2 |
0.4 |
0.6 |
5 |
0.2 |
4. Теоретические расчеты
Определим ![]() =
=![]() при котором разделение
движений справедливо (для пункта 3 лабораторной работы).
при котором разделение
движений справедливо (для пункта 3 лабораторной работы).
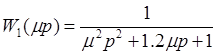 ,
, 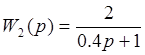 ,
, 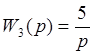
Приведем систему к дифференциальной системе уравнений стандартного вида:
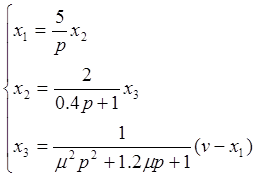
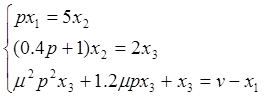
Мы получили систему
четвертого порядка, поэтому для введения четвертого уравнения проведем замену
переменной: ![]() .
.
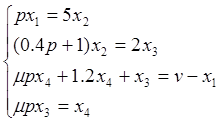
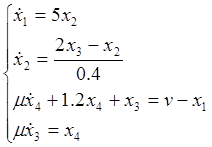 (1)
(1)
Это система дифференциальных уравнений исследуемой системы в стандартном виде.
Считая ![]() в системе уравнений (1), получим
подсистему медленных движений системы:
в системе уравнений (1), получим
подсистему медленных движений системы:
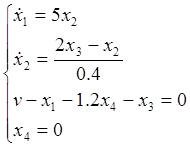
Упростим:
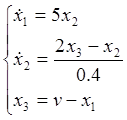
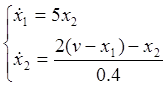 (2)
(2)
Преобразуем систему (2) к матричному виду и найдем корни ее характеристического полинома:
![]()
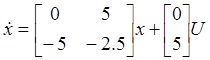
Получим характеристическое уравнение:
![]()
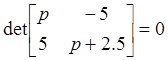
![]() его
корни:
его
корни:
![]() (3)
(3)
Получим из (1) подсистему быстрых движений. Перейдем к новой переменной времени:
![]() ,
, ![]() , следовательно
, следовательно 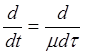
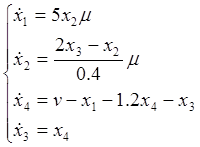
Считая ![]() , получим:
, получим:
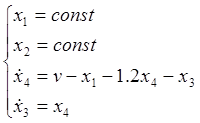
Вернемся к старому времени:
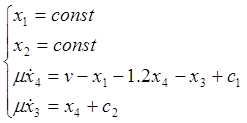 (4)
(4)
Полученная нами система (4) и есть подсистема быстрых движений. Перейдем к матричной форме:
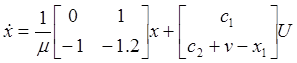
Найдем корни характеристического уравнения:
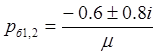 (5)
(5)
Перейдем от корней быстрой (5) и медленной (3) составляющей к среднеквадратичным корням:
![]()
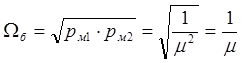
Для справедливости разделения движений принято считать:
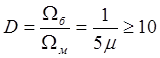
Возьмем ![]() , Тогда
, Тогда ![]() .
.
Определим ![]() =
=![]() при котором разделение
движений справедливо (для пункта 9 лабораторной работы).
при котором разделение
движений справедливо (для пункта 9 лабораторной работы).
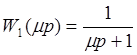 ,
, 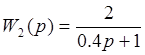 ,
, 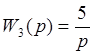
Перейдем к дифференциальным уравнениям:
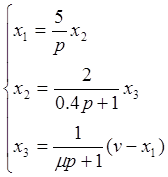
Приведем к стандартному виду:
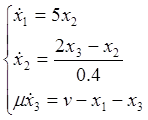
Подсистема медленных движений:
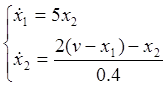
Корни ![]()
Подсистема быстрых движений:
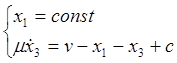
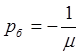
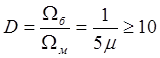
Возьмем ![]() , Тогда
, Тогда ![]() .
.
5. Выполнение работы.
5.1. Построение модели системы по структурной схеме:
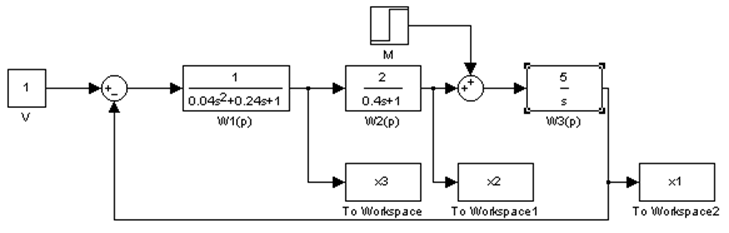
Оценка качества переходного процесса по переменным x1, x2, x3 при n = 1 и M(t) = 0
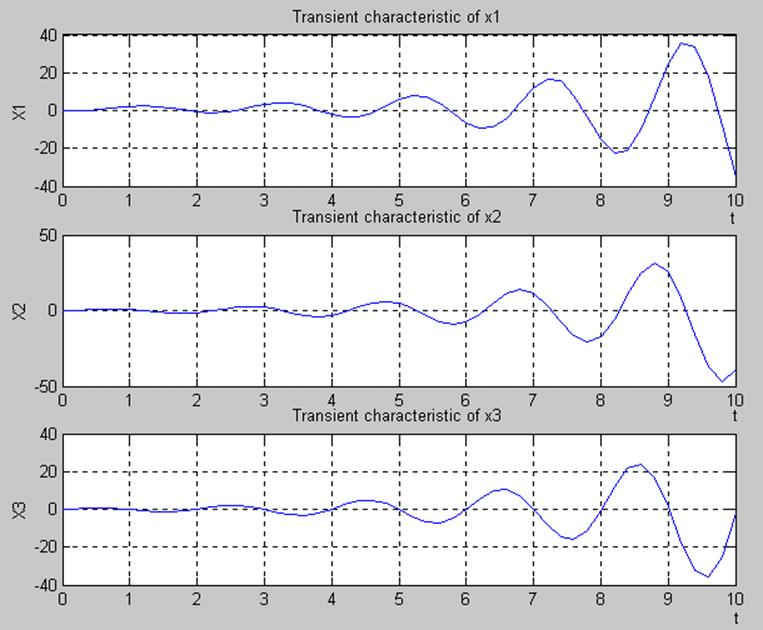
Построение фазового портрета системы на плоскость (x1, x3):
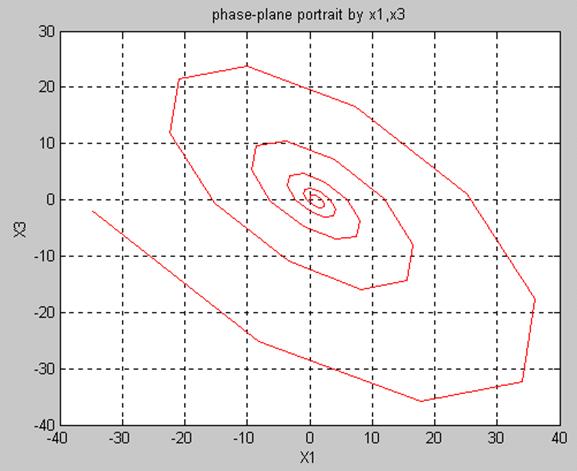
5.2. Уменьшая последовательно ![]() в 5,
10, 40 раз снимаем процессы x1(t),
x2(t), x3(t)
в 5,
10, 40 раз снимаем процессы x1(t),
x2(t), x3(t)
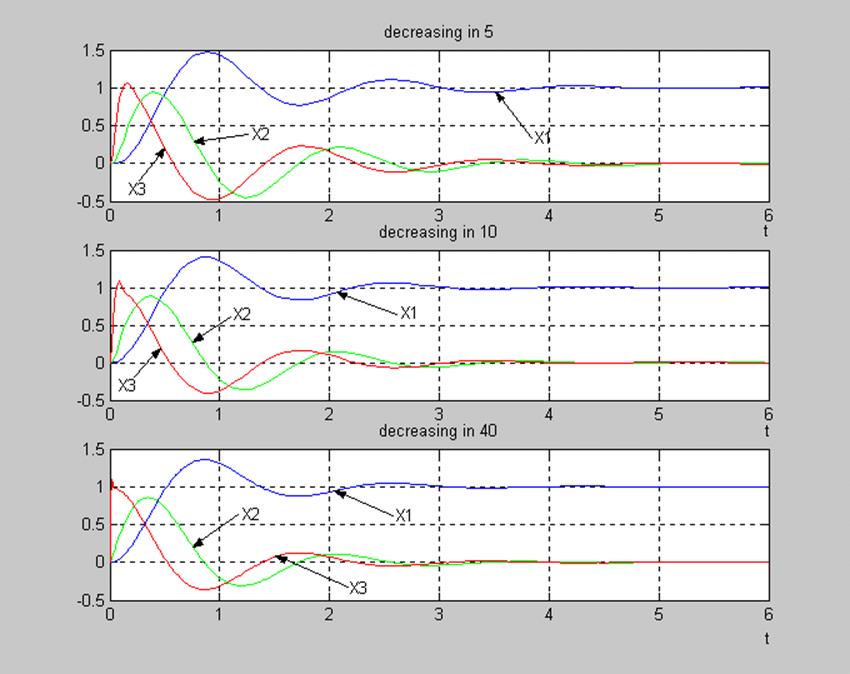 |
Фазовые
портреты (x1 , x3)
при различных значениях ![]()
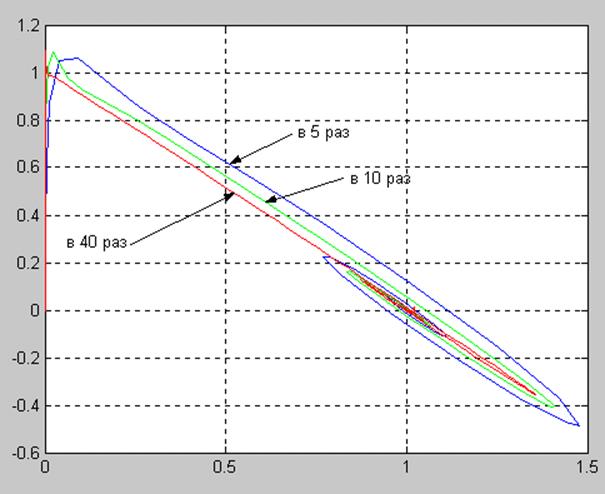
5.3. Оценка качества переходных процессов для переменных x1(t) и x3(t)
при расчитанном значении m = m0 = 0.0167
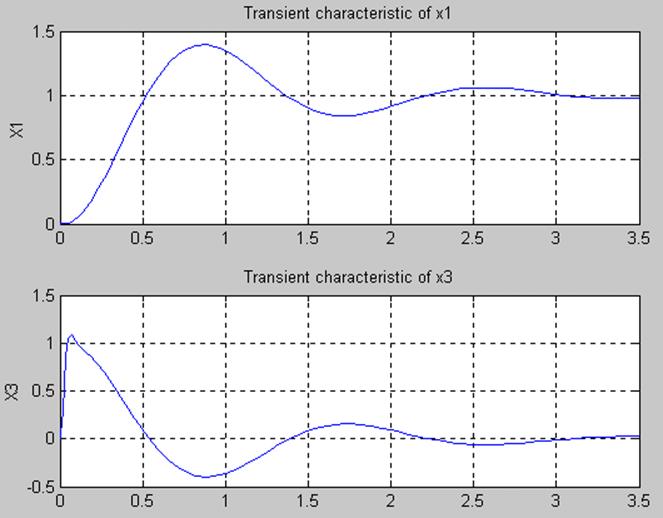
для x1 : tп = 3c. s = 40%
для x3 : tп = 2c. s = %
5.4. Исследоваине влияния параметра d, изменя его значения в диапазоне (0.1 ; 1) на фазовый портрет и переходные процессы x1(t) и x3(t)
Переходные процессы x1(t), x3(t) при d=0,1; 0.2; 0.6; 0.8; 1
|
|
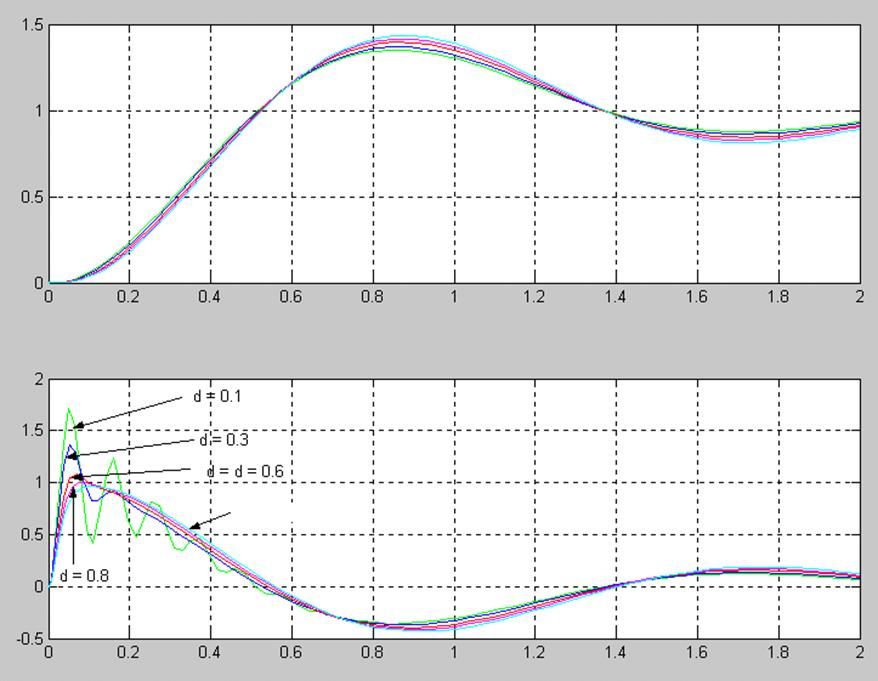
Фазовые портреты x1(t), x3(t) при d=0,1; 0.2; 0.6; 0.8; 1
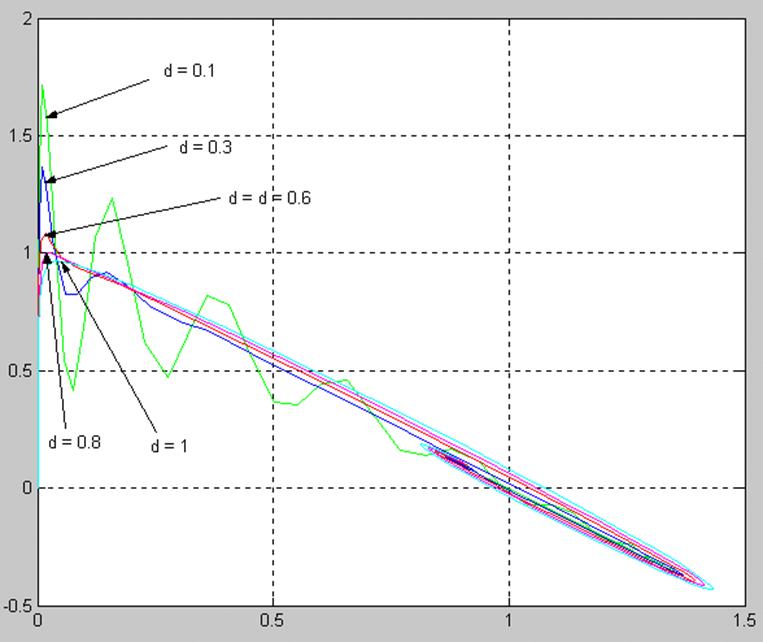
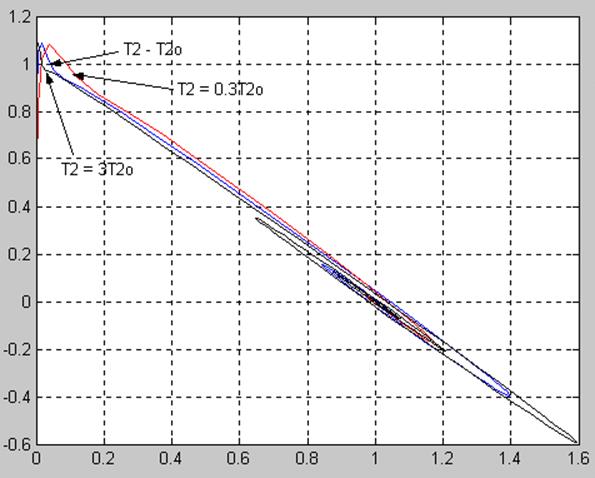
5.5 Исследование влияния параметра T2 на фазовый портрет системы, а также медленную и быструю составляющие движения.
Переходные процессы в системе при различных T2
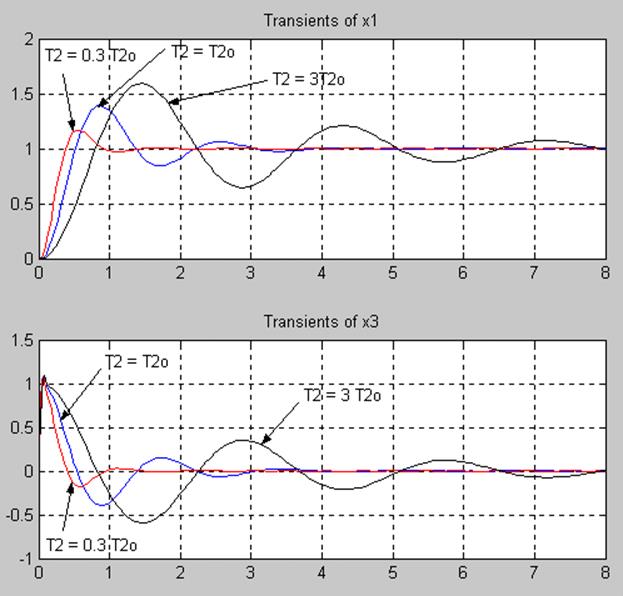
Фазовые портреты системы при различных T2.
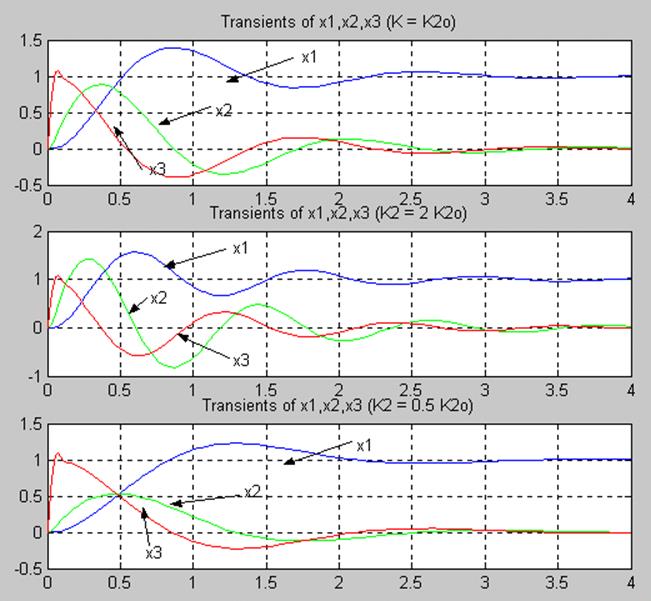
5.6 Влияние параметра К2 на переходные процессы для переменных
x1(t), x2(t), x3(t)
при ![]() =
=![]() 0
0
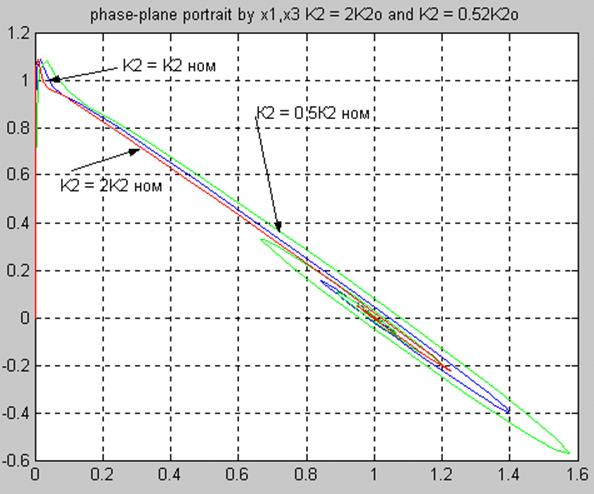
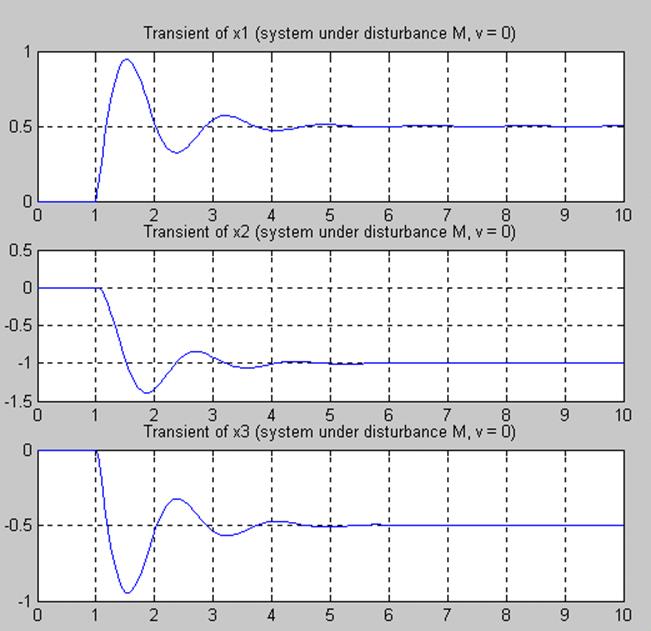
5.7 Фазовый портрет и переходные характеристики
x1(t), x2(t), x3(t)
при ![]() =
=![]() 0, v=0, M(t-t) = 1 (t = 1)
0, v=0, M(t-t) = 1 (t = 1)
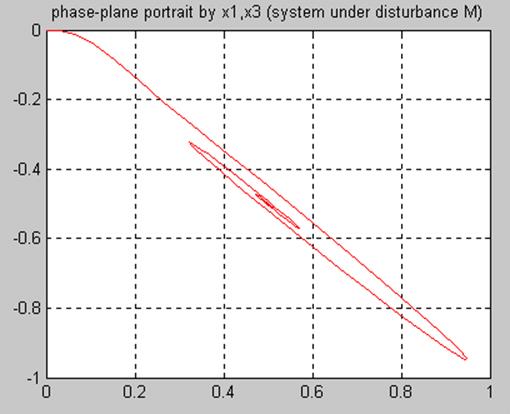
5.8 Разделение движений и исследование порознь быстрой и
медленной составляющей движения.
|
ПМД.
Tp=6 σ=35% |
ПБД.
Tp=0.6 σ=5% |
5.9 Замена колебательного звена на входе системы апериодическим с передаточной функцией:
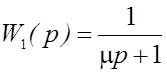
оценка качества переходных процессов.
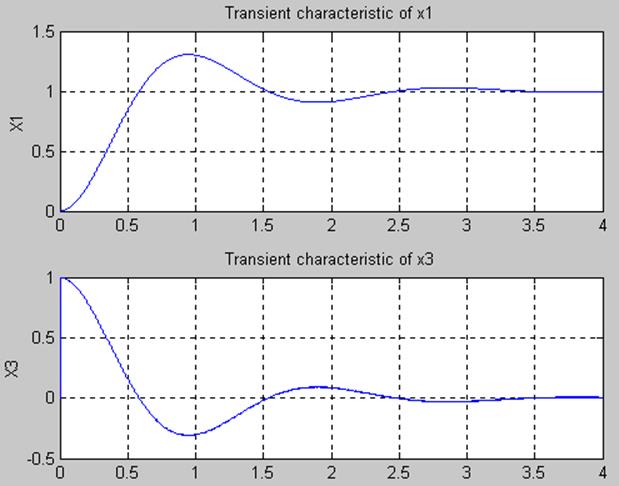
для x1 : tп = 2c. s = 20%
для x3 : tп = 1,5c. s = 20 %
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.