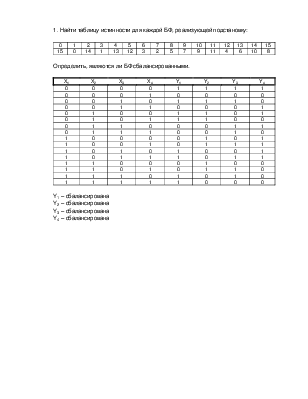














1. Найти таблицу истинности для каждой БФ, реализующей подстановку:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
15 |
0 |
14 |
1 |
13 |
12 |
3 |
2 |
5 |
7 |
9 |
11 |
4 |
6 |
10 |
8 |
Определить, являются ли БФ сбалансированными.
|
X1 |
X2 |
X3 |
X4 |
Y1 |
Y2 |
Y3 |
Y4 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Y1 – сбалансирована
Y2 – сбалансирована
Y3 – сбалансирована
Y4 – сбалансирована
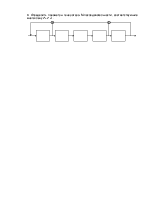
2. Найти таблицу истинности для каждой БФ, реализующей подстановку:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
10 |
13 |
0 |
3 |
6 |
9 |
12 |
15 |
2 |
5 |
8 |
11 |
14 |
1 |
4 |
7 |
Определить, являются ли подстановка
а) инволюцией;
б) биективной.
|
X1 |
X2 |
X3 |
X4 |
Y1 |
Y2 |
Y3 |
Y4 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
Y1 – сбалансирована
Y2 – сбалансирована
Y3 – сбалансирована
Y4 – сбалансирована
Все функции сбалансированы – подстановка биективна
Функция не является инволюцией, т.к. f(f(x))¹x
(например, 0®10, а 10®8 (а не в 0))
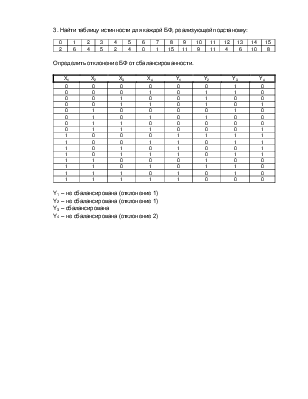
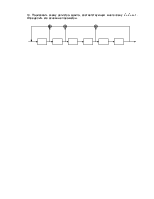
3. Найти таблицу истинности для каждой БФ, реализующей подстановку:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.