обозначим через (Lk , f(k)(x)) регистр сдвига минимальной длины, генерирующий a1,…, ak. Примем за предположение индукции, что
Lk=max[Lk-1, k-Lk-1], k=1,…,r-1 ,
каждый раз, когда f(k) (x) ≠f(k-1)(x). Это, очевидно, верно для k=0, если a1 отличен от нуля, поскольку L0=0 и L1 =1. В более общем случае, если аi-первый ненулевой элемент в заданной последовательности, то Li-1=0 и Li =i . Тогда предположение индукции относится к индукции k=i. Значение k в последней итерации, приведшей к изменению длины, будем обозначать через m. Последнее означает, что при завершении (r-1)-й итерации m является целым числом, таким, что
Lr-1=Lm>Lm-1.
Теперь имеет место следующее равенство:
a1+
![]() (r-1)aj-i=
(r-1)aj-i=![]() (r-1)aj-i=
(r-1)aj-i= ![]()
Если ![]() =0, то регистр (Lr-1,f(-1)(x)) также генерирует
первые r символов, и таким
образом,
=0, то регистр (Lr-1,f(-1)(x)) также генерирует
первые r символов, и таким
образом,
Lr=Lr-1 и f(r)(x) = f(r-1)(x).
Если ![]() ≠0, то необходимо построить новый регистр
сдвига. Поскольку изменение длины регистра сдвига произошло при k=m. Следовательно,
≠0, то необходимо построить новый регистр
сдвига. Поскольку изменение длины регистра сдвига произошло при k=m. Следовательно,
ai+![]() i(m-1)aj-i=
i(m-1)aj-i=![]()
и по предложению индукции
Lr-1=Lm=max [Lm-1,m-Lm-1]=m-Lm-1,
поскольку Lm>Lm-1. Новый многочлен :
f(r)
(x)=f(r-1)(x)-![]() -1xr-mf(m-1)(x)
-1xr-mf(m-1)(x)
и пусть Lr=deg f(r)(x). В этом случае поскольку deg f(r-1)(x)≤Lr-1 и deg[xr-mf(m-1)(x)]≤r-m+Lm-1, то
Lr≤max [Lr-1,r-m+Lm-1] ≤max[Lr-1,r-Lr-1].
Из теоремы 1 при условии, что (Lr,f(r)(x)) генерирует a1,…,ar, следует, что Lr=max [Lr-1, r-Lr-1]. Осталось только доказать, что регистр сдвига (Lr,f(r)(x)) генерирует требуемую последовательность. Доказывается это непосредственным вычислением разности между aj и сигналом на выходе обратной связи регистра сдвига:
aj-(-![]() i(r)aj-i)=ai+
i(r)aj-i)=ai+![]() i(r-1)aj-i-
i(r-1)aj-i-![]() -1[ai-r+m+
-1[ai-r+m+![]() i(m-1)ai-r+m-i]=
i(m-1)ai-r+m-i]=![]()
Регистр (Lr, f(n)(x)) генерирует a1,…,ar. В частности, (Ln, f(n)(x)) генерирует a1,…,an и теорема доказана.
Пусть заданы a1,…,an из некоторого поля, и пусть при начальных условиях f(0)(x)=1, t(0)(x) =1 и L0=0 выполняются следующие рекуррентные равенства, используемые для вычисления f(n)(x):
![]() =
=![]() i(r-1)ar-1 ,
i(r-1)ar-1 ,
Lr=бr(r-Lr-1)+(1- бr)Lr,
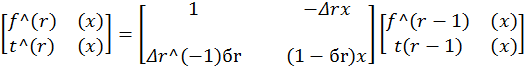 ,
,
r =1,…, 2n, где
бr =1, если одновременно ![]() ≠0 и 2Lr-1≤r-1, и бr=0 в
противном случае. Тогда f(2r)(x) является многочленом
наименьшей степени, коэффициенты которого удовлетворяют равенствам f0(2r)=1
и ar+
≠0 и 2Lr-1≤r-1, и бr=0 в
противном случае. Тогда f(2r)(x) является многочленом
наименьшей степени, коэффициенты которого удовлетворяют равенствам f0(2r)=1
и ar+![]() i(2r)ar-1 =0, r=L2r+1,…, 2r. Доказательство следует из теоремы 2.
i(2r)ar-1 =0, r=L2r+1,…, 2r. Доказательство следует из теоремы 2.
В этой теореме ![]() может
обращаться в нуль, но только в том случае, когда бr=0.
Положим тогда по определению
может
обращаться в нуль, но только в том случае, когда бr=0.
Положим тогда по определению ![]() -1
бr =0.
Блок-схема алгоритма Берлекэмпа-Месси приведена на рисунке 4. На r-м шаге указанный алгоритм содержит число умножений, равное
примерно удвоенной степени многочлена f(r)(x). Степень многочлена f(r)(x) равна примерно r/2, и всего
имеется 2n итераций, так что
всего алгоритм содержит примерно 2n2=
-1
бr =0.
Блок-схема алгоритма Берлекэмпа-Месси приведена на рисунке 4. На r-м шаге указанный алгоритм содержит число умножений, равное
примерно удвоенной степени многочлена f(r)(x). Степень многочлена f(r)(x) равна примерно r/2, и всего
имеется 2n итераций, так что
всего алгоритм содержит примерно 2n2=![]() умножений
и примерно такое же число сложений. Можно сказать, что порядок числа умножений
в алгоритме Берлекэмпа-Месси равен n2, или
формально , O(n2).
умножений
и примерно такое же число сложений. Можно сказать, что порядок числа умножений
в алгоритме Берлекэмпа-Месси равен n2, или
формально , O(n2).
Реализовать алгоритм Берлекэмпа –Месси на произвольных значениях.
Лабораторная работа выполнена на Mapple 13.
> Berlekamp(x^31-1,x)mod 2;
> alias(a=RootOf(x^5+x^4+x^3+x^2+1)mod 2);
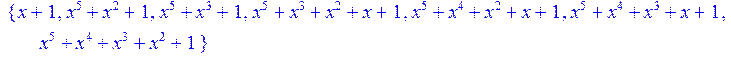
![]()
> for i from 0 to 30 do y[i]:= Rem(x^i,x^5+x^4+x^3+x^2+1,x) mod 2 od;
>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> n:=31;#длина кода
![]()
> k:=21;d:=11;#число информационных символов и расстояние Хемминга
![]()
![]()
>
> #генераторный полином
> g1:=(x-a)*(x-a^2)*(x-a^3)*(x-a^4)*(x-a^5)*(x-a^6)*(x-a^7)*(x-a^8)*(x-a^9)*(x-a^10);
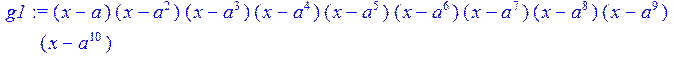
> g2:= expand(g1)mod 2;#умножение
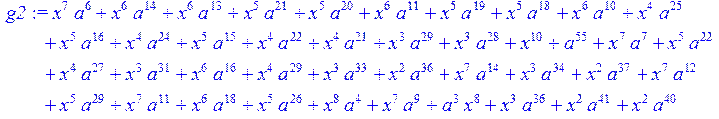

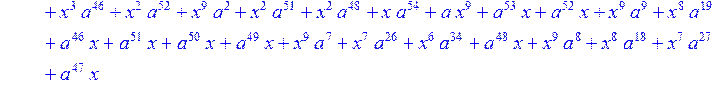
> g3:= collect (g2,x)mod 2;#вычисление коэффициентов при x
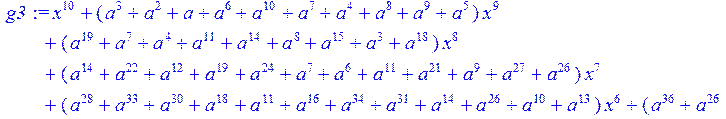
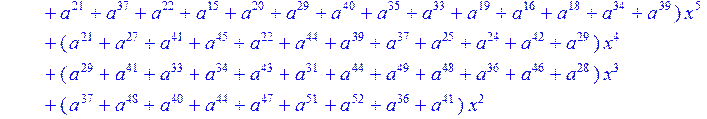
![]()
> g4:= simplify (g3)mod 2;#раскрытие скобок
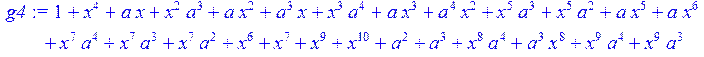
> g5:= collect (g4,x)mod 2;#вычисление коэффициентов
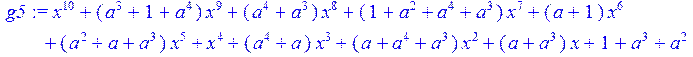
> g:=collect(simplify (g5),x)mod 2;
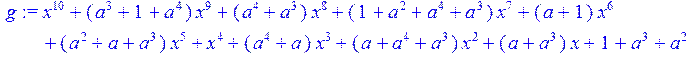
>
>
>
>
> m:=m0+x*m1+x^2*m2+x^3*m3+x^4*m4+x^5*m5;#общий вид сообщения
![]()
> m0:=a^3;m1:=a^2;m2:=a;m3:=a^4;m4:=a^2;m5:=a;#произвольные коэффициенты
![]()
![]()
![]()
![]()
![]()
![]()
> m;
![]()
> c:=m*g5;#получение кодового слова
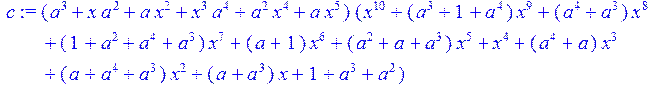
> c1:= expand (c)mod 2;
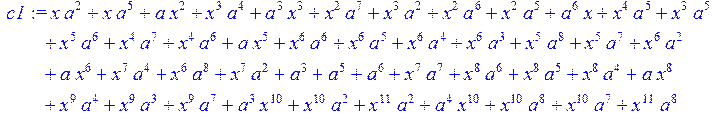
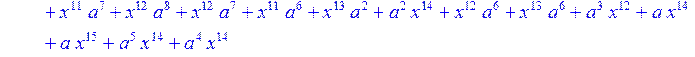
> c2:= simplify (c1)mod 2;
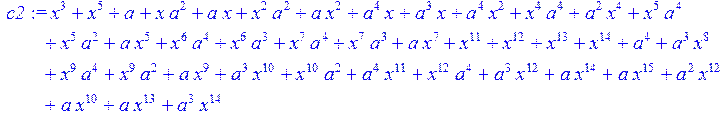
> c3:= collect (c2,x) mod 2;

>
>
> sort (c3);
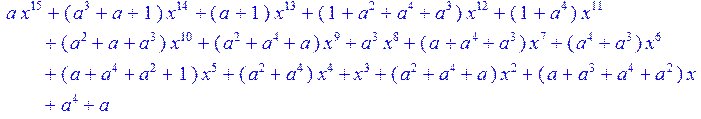
> for i from 0 to 30 do v[i]:=(x-a^(i)) od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> for i from 0 to 30 do R[i]:=Quo(x^31-1,v[i],x)mod 2;r[i]:=Rem(R[i],v[i],x)mod 2 od;#строим вспомогательные полиномы для базиса
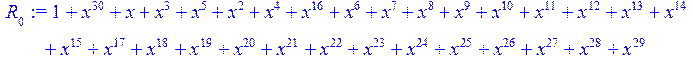
![]()
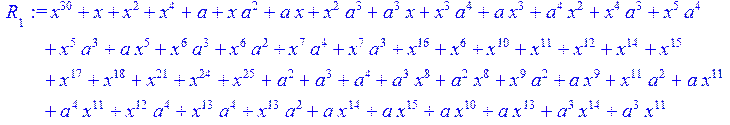

![]()
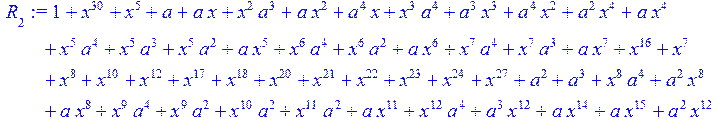
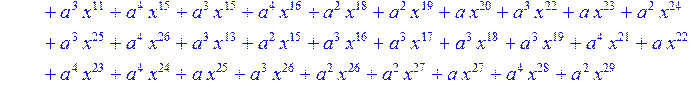
![]()
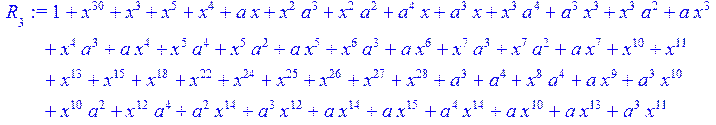
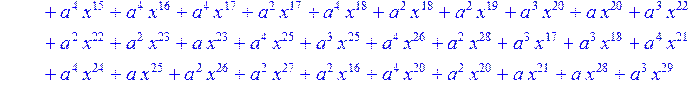
![]()

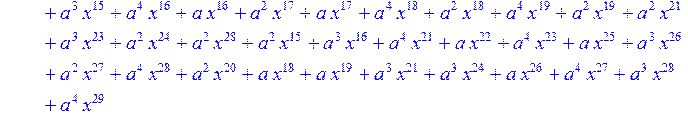
![]()
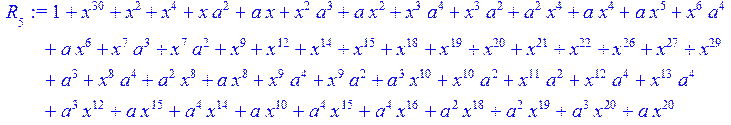
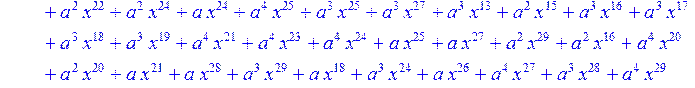
![]()
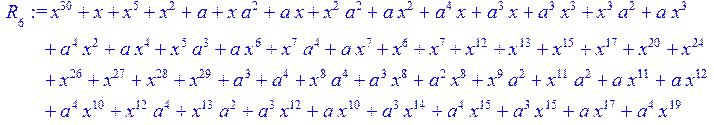
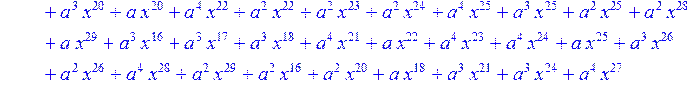
![]()
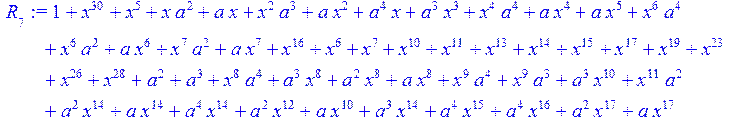
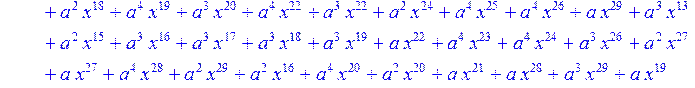
![]()
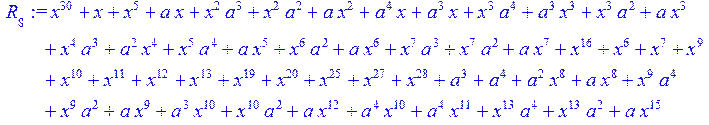
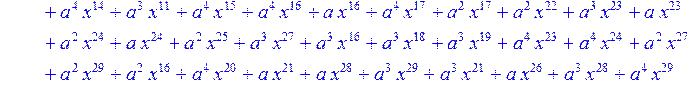
![]()

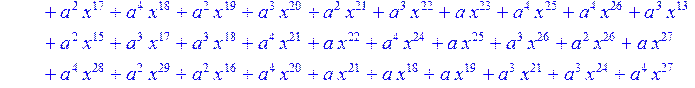
![]()
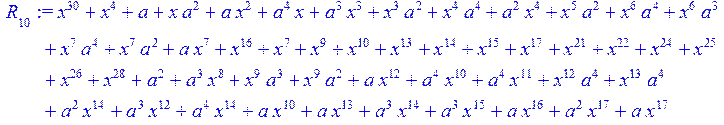

![]()
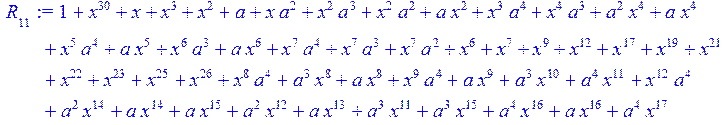
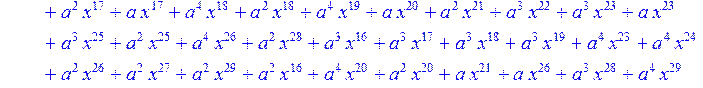
![]()
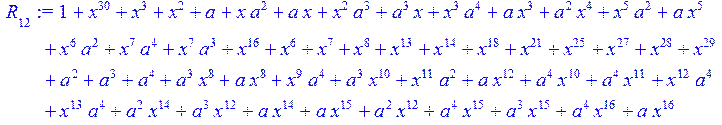
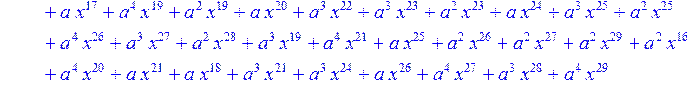
![]()
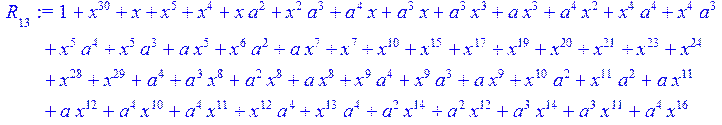

![]()
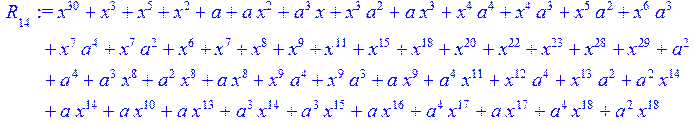
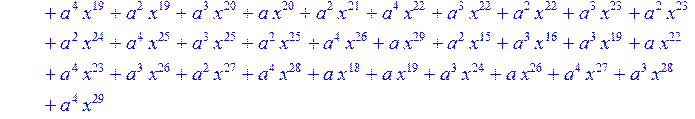
![]()
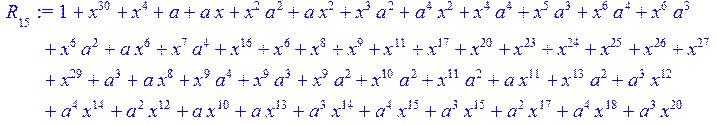
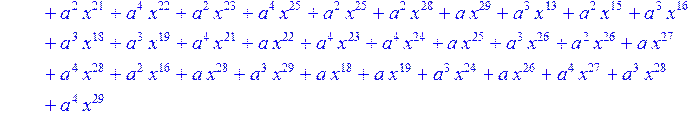
![]()
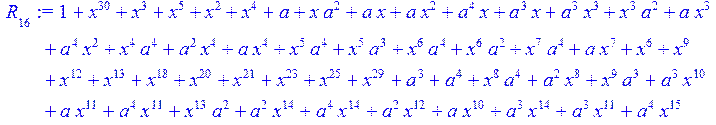
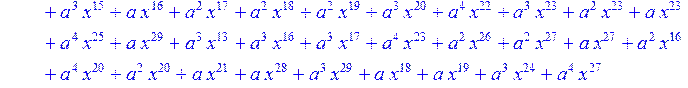
![]()
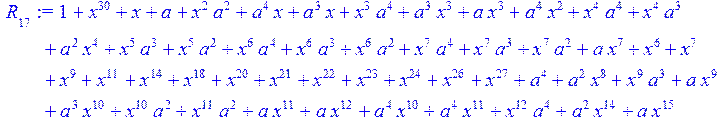
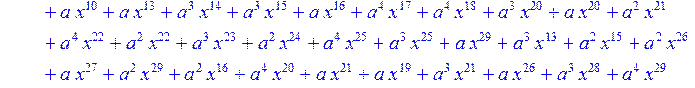
![]()
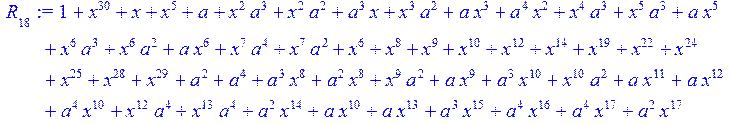
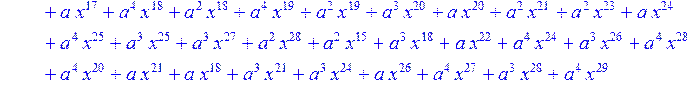
![]()
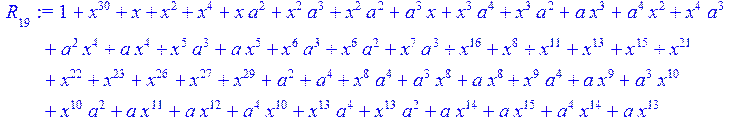
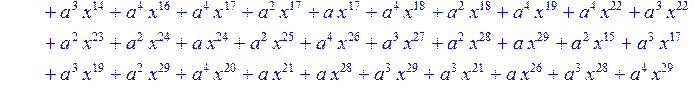
![]()
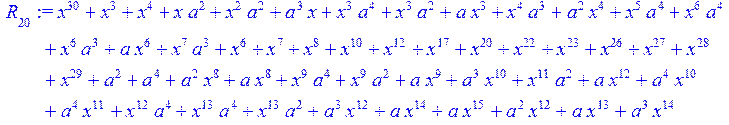
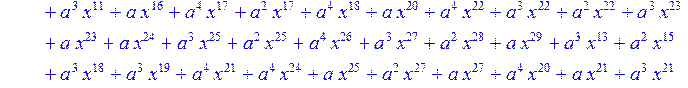
![]()
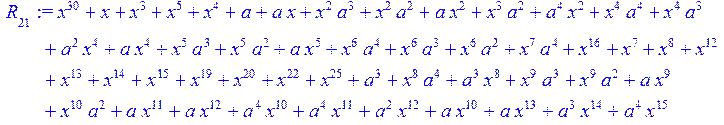
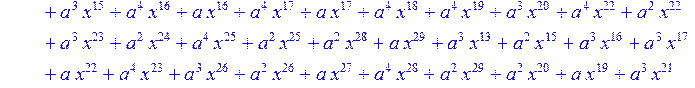
![]()

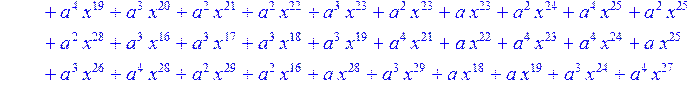
![]()
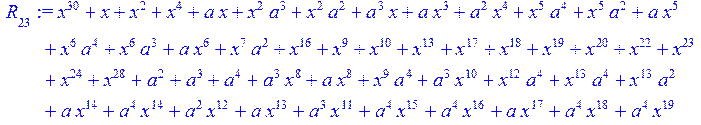
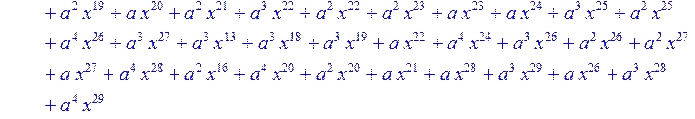
![]()
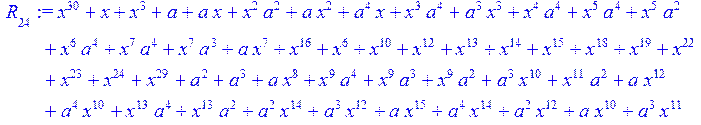
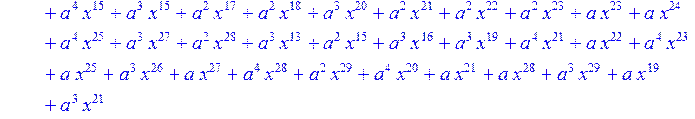
![]()
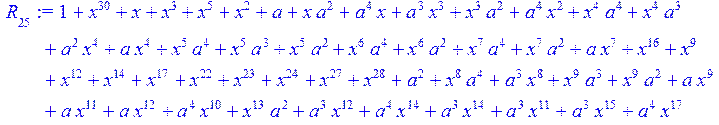
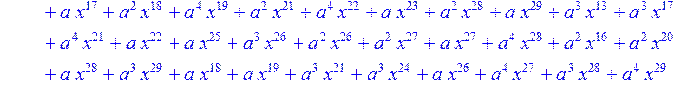
![]()
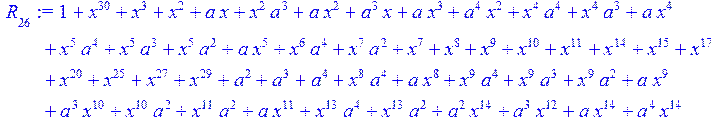
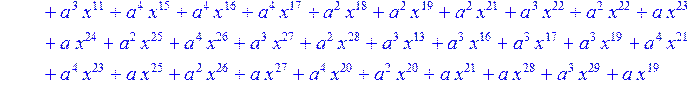
![]()
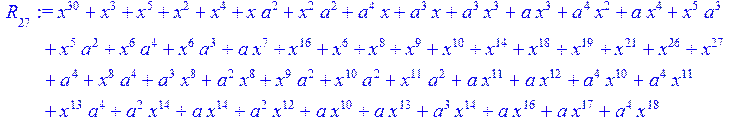
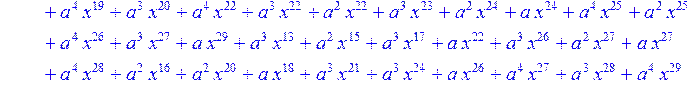
![]()
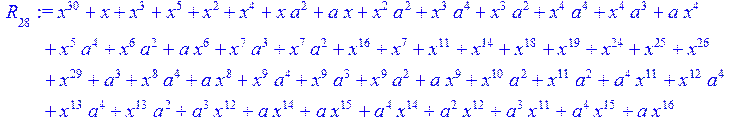
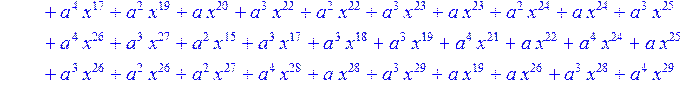
![]()
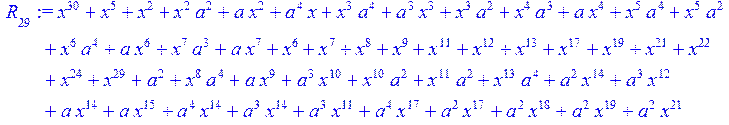
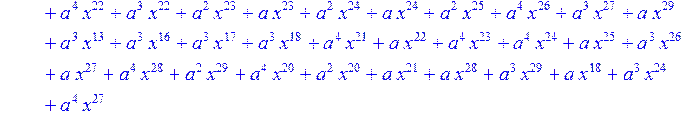
![]()

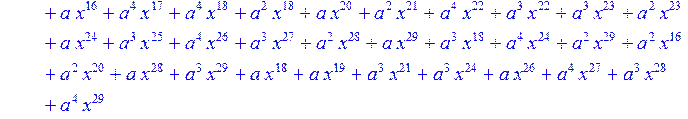
![]()
> #Базис для преобразования Фурье.
> for i from 0 to 30 do B[i]:=Quo(R[i],r[i],x)mod 2 od;
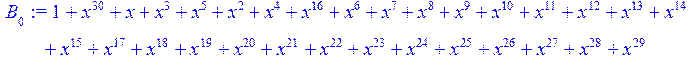
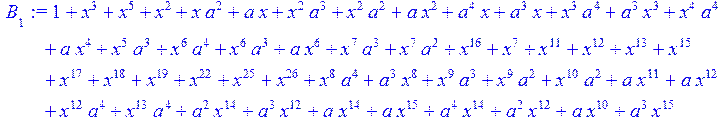
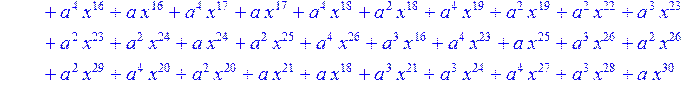
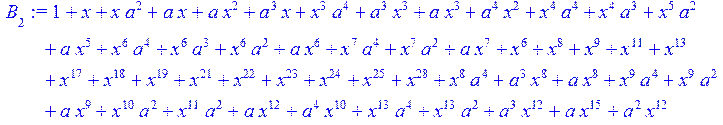
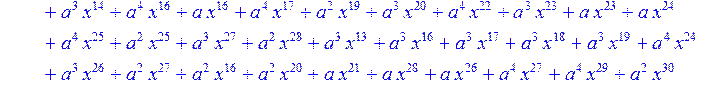
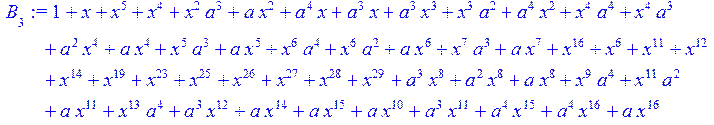
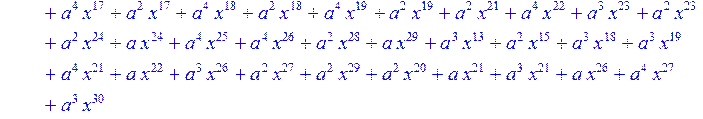
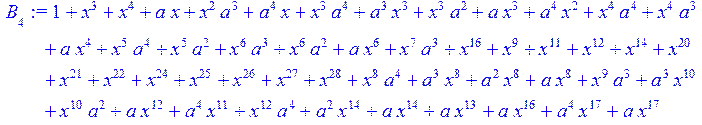
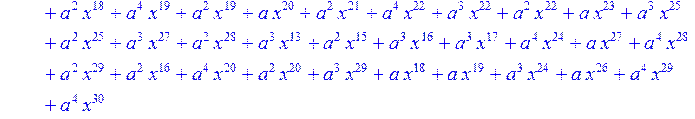
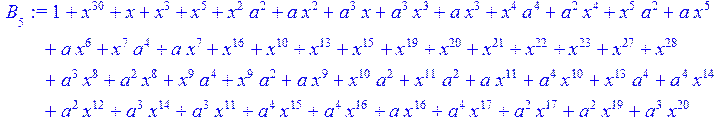
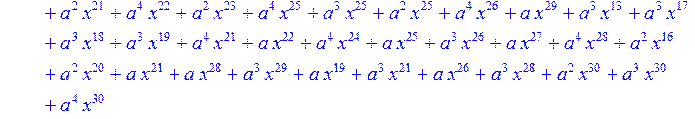
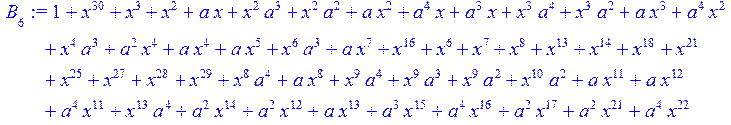

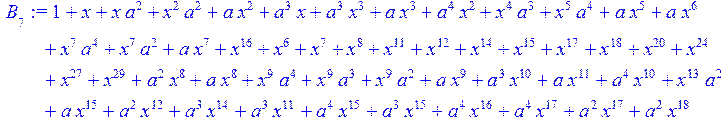
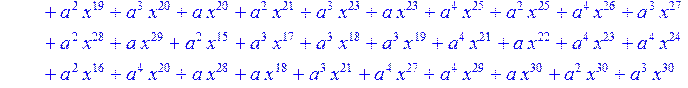

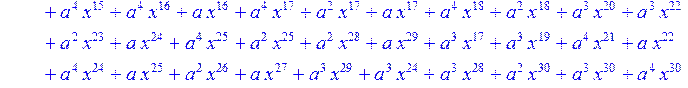
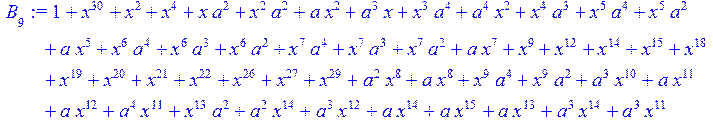
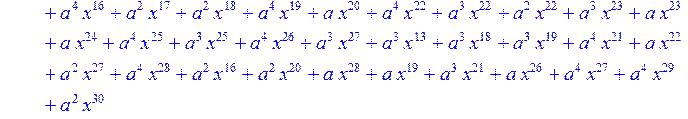
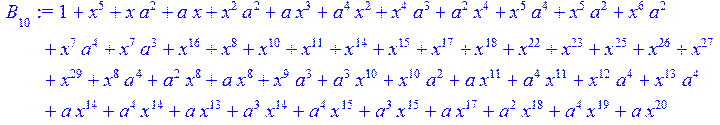
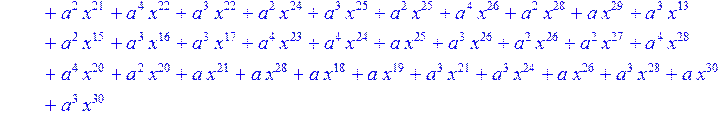
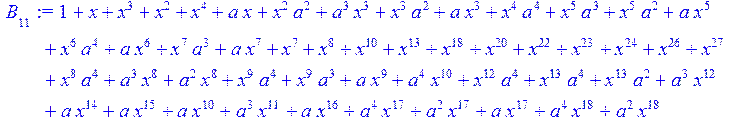
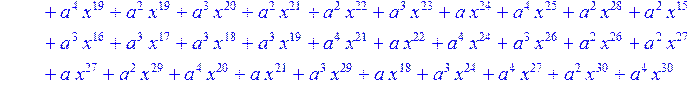
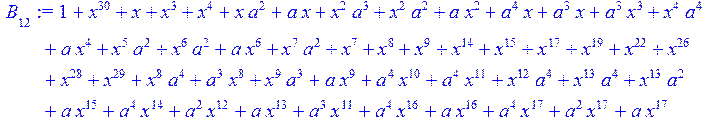
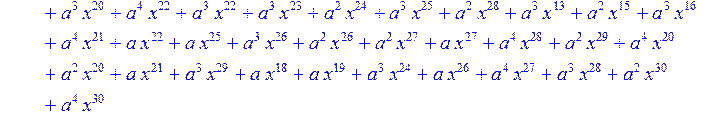
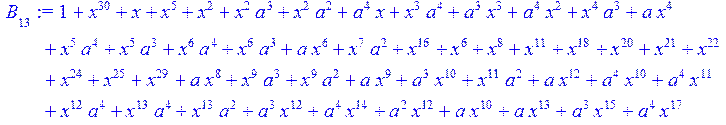
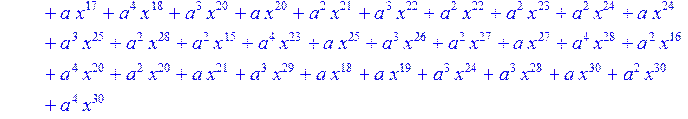
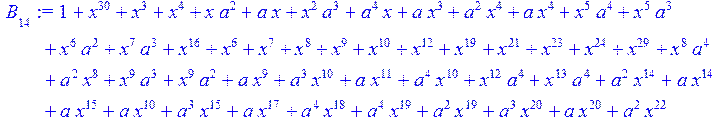
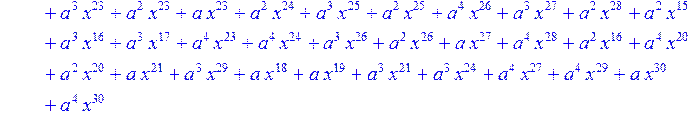

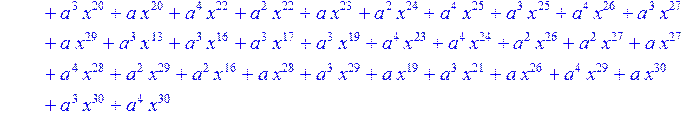
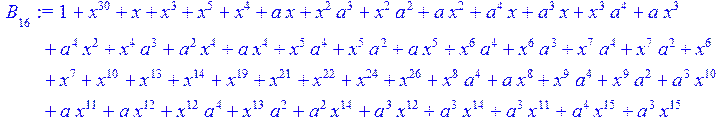
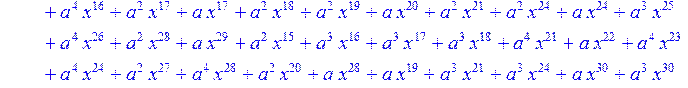
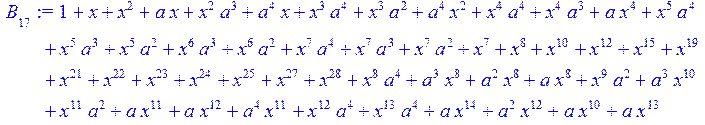
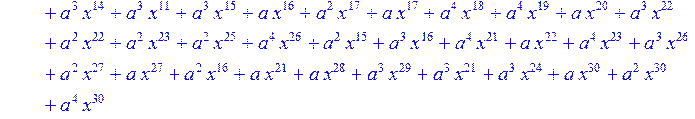

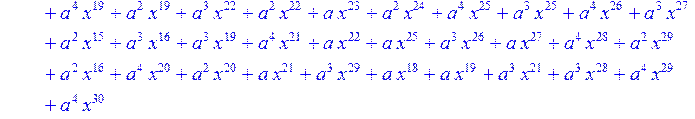
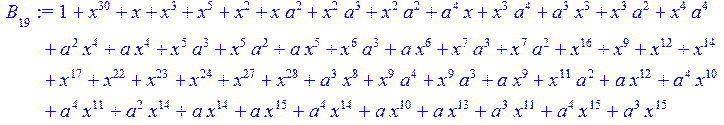
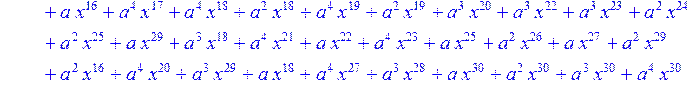
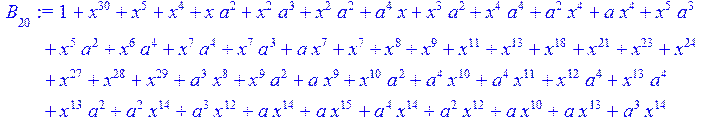
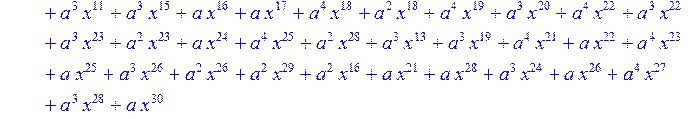
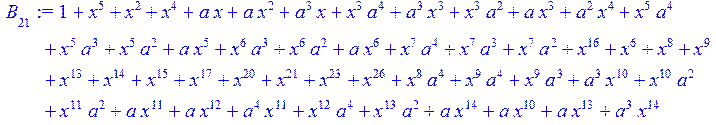
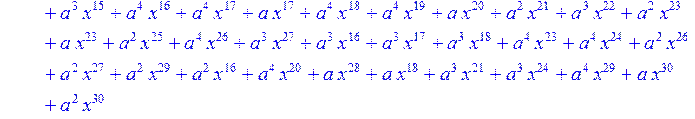
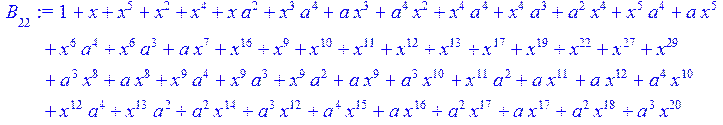
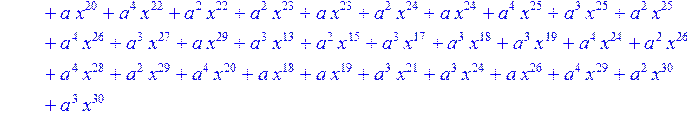
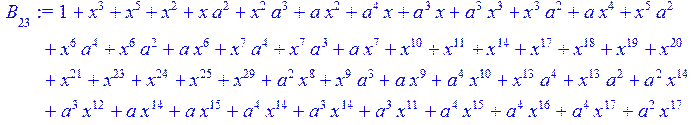
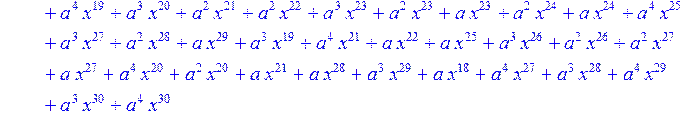
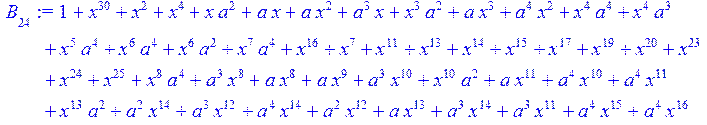
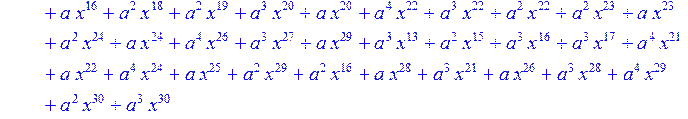
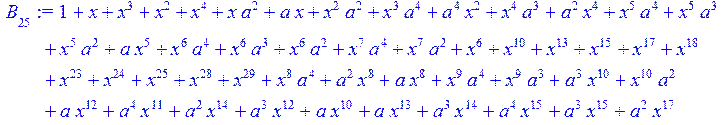
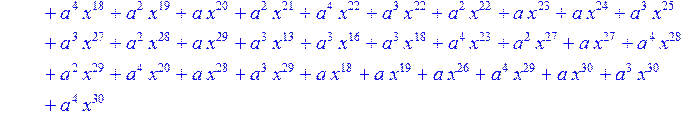
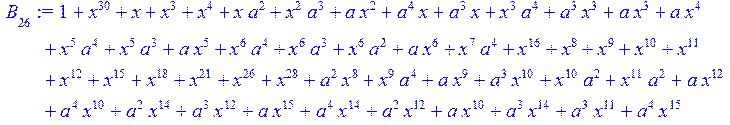
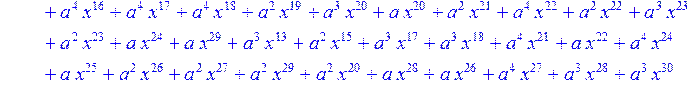
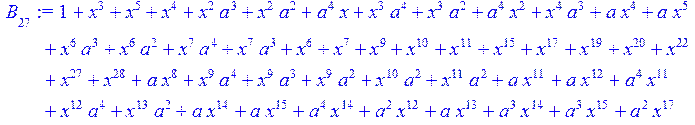
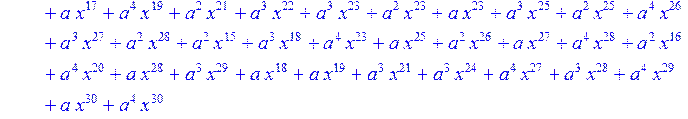

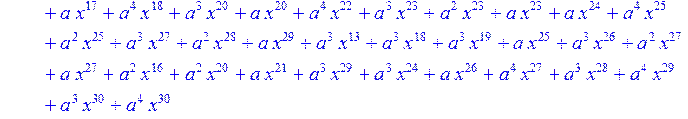
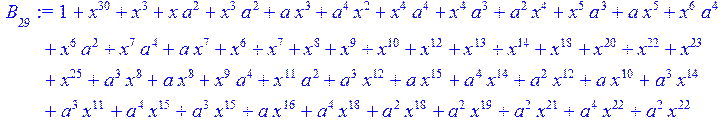
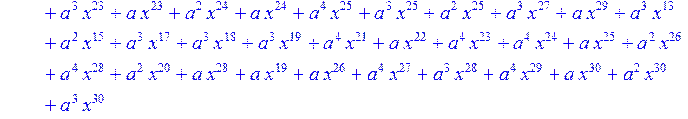
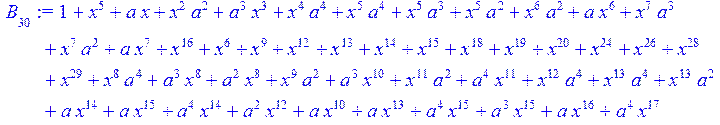
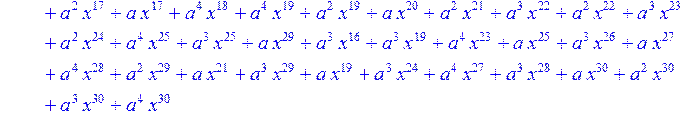
> #Преобразование Фурье от принятого кодового слова.
> for i from 0 to 30 do f[i]:=Rem (c,v[i],x)mod 2 od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> #Обратное преобразование Фурье.С-кодовое слово
> C:=(f[0]*B[0]+f[1]*B[1]+f[2]*B[2]+f[3]*B[3]+f[4]*B[4]+f[5]*B[5]+f[6]*B[6]+f[7]*B[7]+f[8]*B[8]+f[9]*B[9]+f[10]*B[10]+f[11]*B[11]+f[12]*B[12]+f[13]*B[13]+f[14]*B[14]+f[15]*B[15]+f[16]*B[16]+f[17]*B[17]+f[18]*B[18]+f[19]*B[19]+f[20]*B[20]+f[21]*B[21]+f[22]*B[22]+f[23]*B[23]+f[24]*B[24]+f[25]*B[25]+f[26]*B[26]+f[27]*B[27]+f[28]*B[28]+f[29]*B[29]+f[30]*B[30])mod 2;
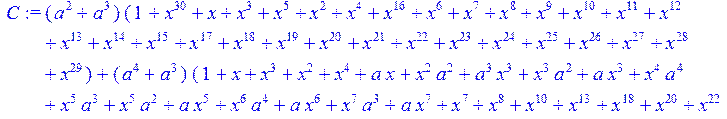
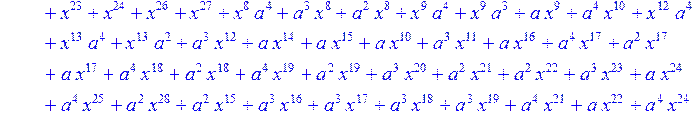
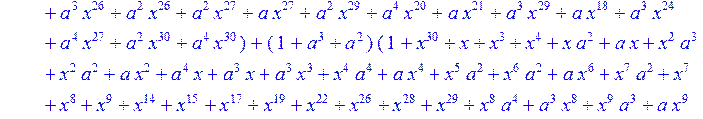
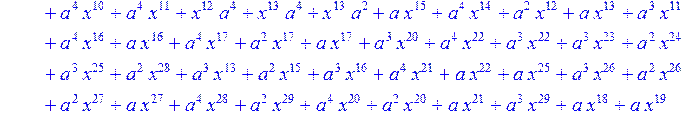
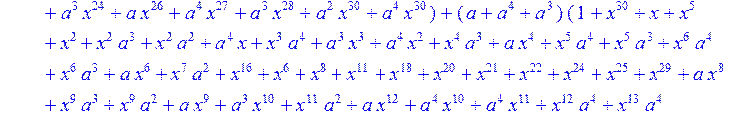
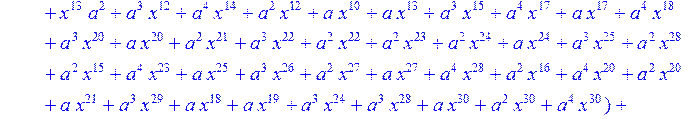
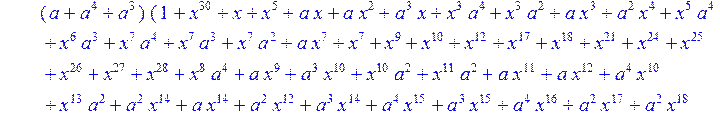
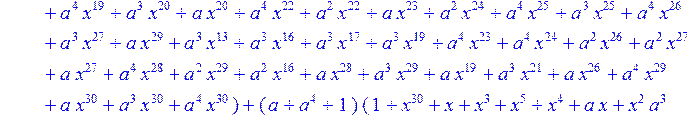
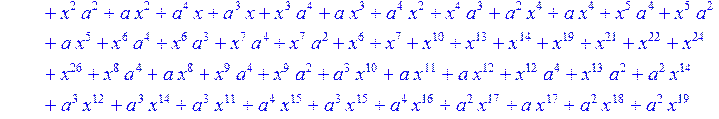
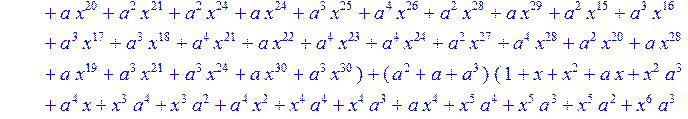
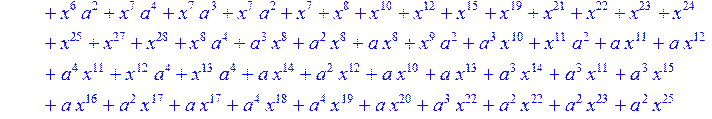

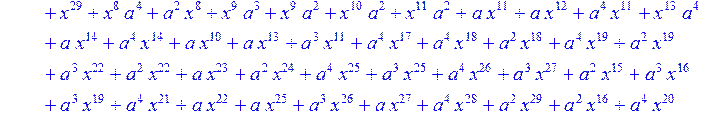
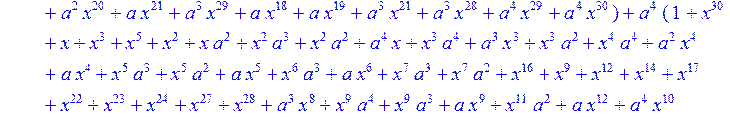
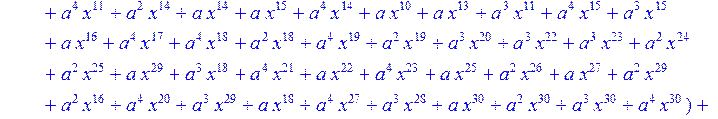
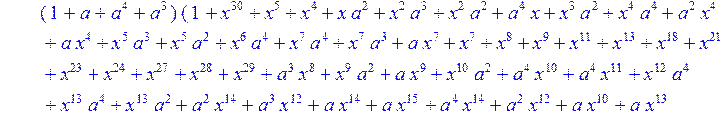
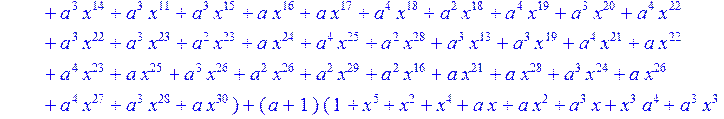
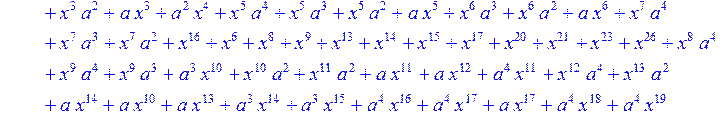
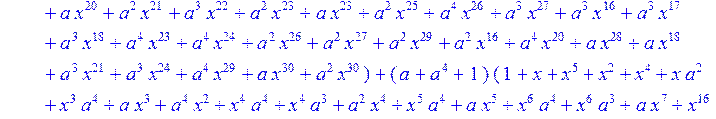

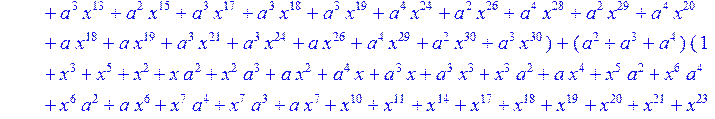
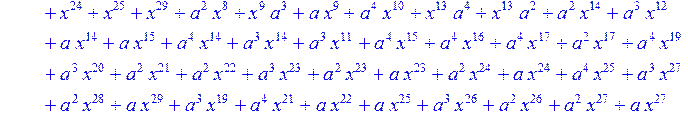
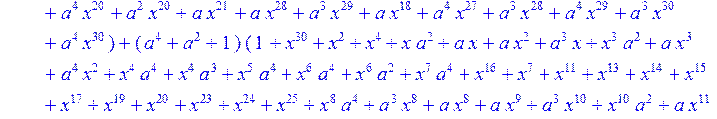
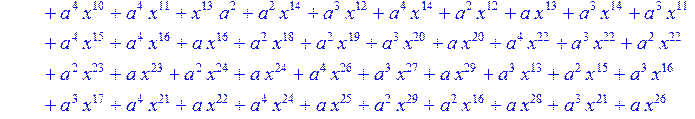
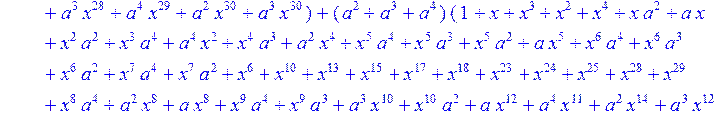
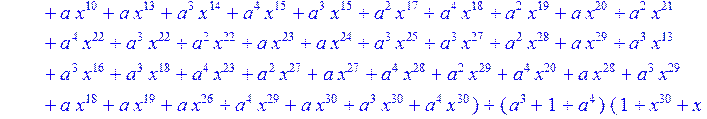
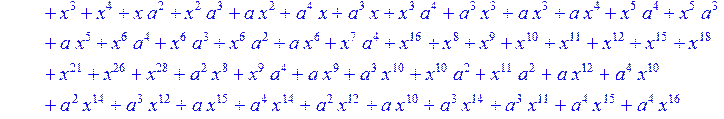
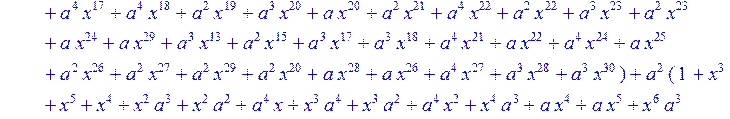
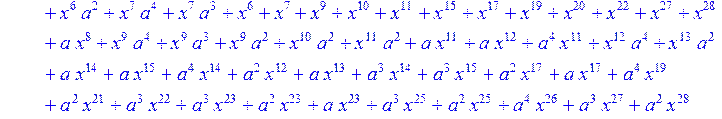
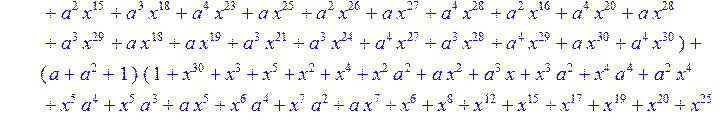
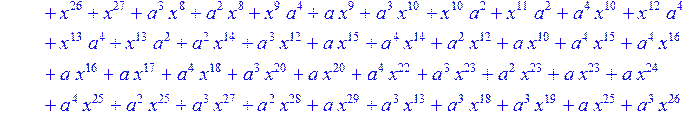
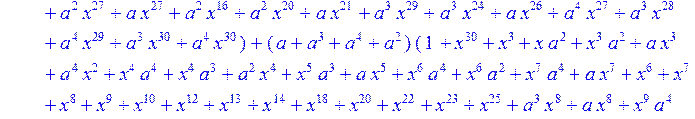
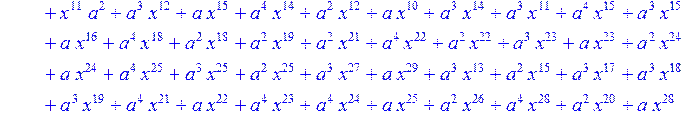
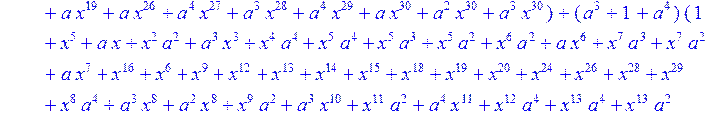
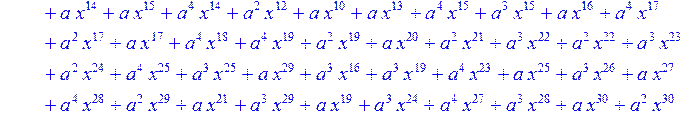
![]()
> C1:=simplify (C)mod 2;
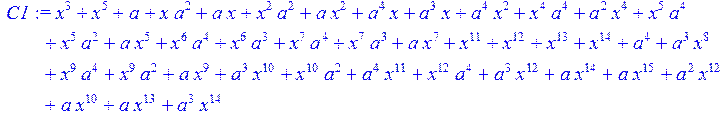
> C2:=collect (C1,x)mod 2;
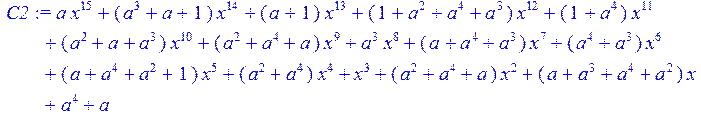
> C3:=(C2-c)mod 2;
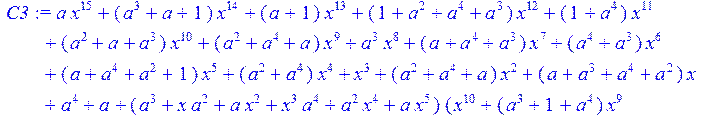
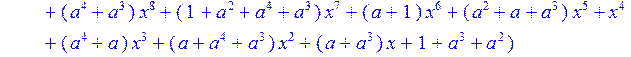
> simplify (C3)mod 2;
![]()
> c;
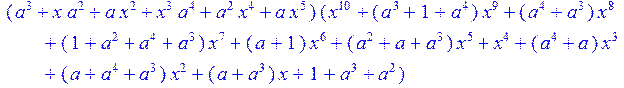
> c3;
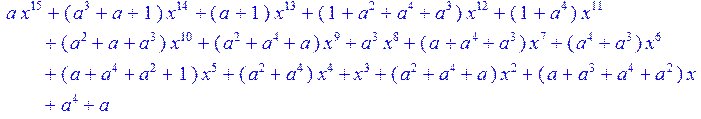
> E:=(a^4*x^2+a^5*x^5+a^6*x^6+a^2*x^7+a^3*x^9);#набор ошибок
![]()
> b:=(c3+E)mod 2;#принятая последоватнльность
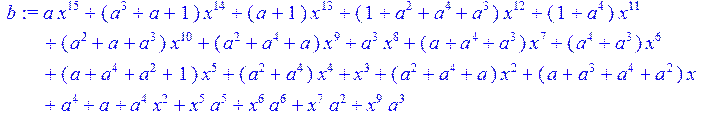
> #Преобразование Фурье в принятой последовательности.
> for i from 0 to 30 do f[i]:=Rem (b,v[i],x)mod 2 od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> #синдром(полином, с коэффициентами относящимися к корням генераторного полинома
> S:=(f[1]+f[2]*x+f[3]*x^2+f[4]*x^3+f[5]*x^4+f[6]*x^5+f[7]*x^6+f[8]*x^7+f[9]*x^8+f[10]*x^9);
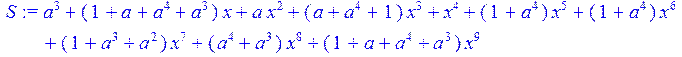
> T:=(x^10);#количество подряд идущих нулей
![]()
>
>
> #Алгоритм Евклида.частное от деления Quo,остаток от деления Rem
> q[1]:= Quo (S,T,x)mod 2;p[1]:=Rem(S,T,x)mod 2;
![]()
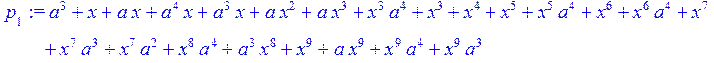
> q[2]:= Quo (T,p[1],x)mod 2;p[2]:=Rem(T,p[1],x)mod 2;
![]()
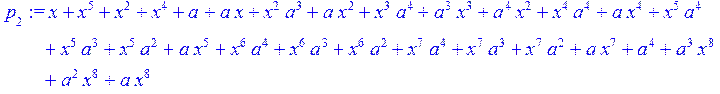
> for i from 1 to 4 do q[i+2]:= Quo (p[i],p[i+1],x)mod 2; p[i+2]:=Rem(p[i],p[i+1],x)mod 2 od;
![]()
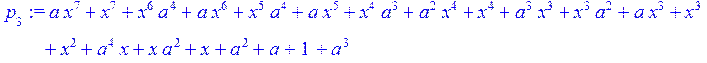
![]()
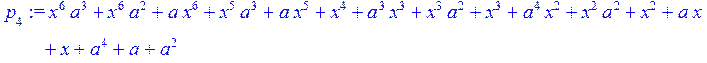
![]()
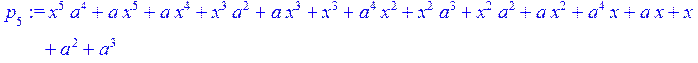
![]()
![]()
>
> Q[0]:=0;Q[1]:=(1);for i from 0 to 4 do Q[i+2]:=collect(simplify((q[i+2]*Q[i+1]+Q[i])),x) od;
![]()
![]()
![]()
![]()
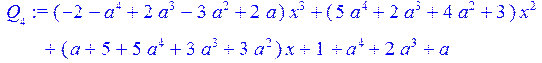
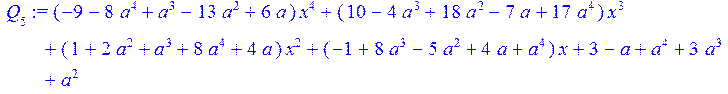
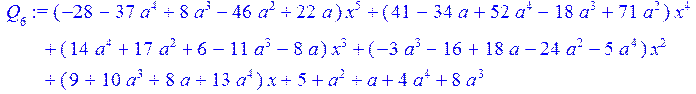
> coeff (Q[6],x,5);#коэффициенты при x^5
![]()
> #Ошибки.
>
> Qn:=Quo (Q[6],coeff (Q[6],x,5),x)mod 2;

> Berlekamp (Qn,x,a)mod 2;
![]()
> i:=Rem ((S)*Qn,T,x)mod 2;
![]()
> u:=Quo (i*(x^31-1),Qn,x) mod 2;
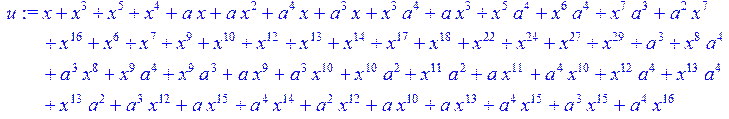
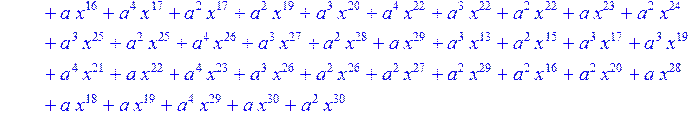
> H1:=sort(collect (u,x)mod 2);
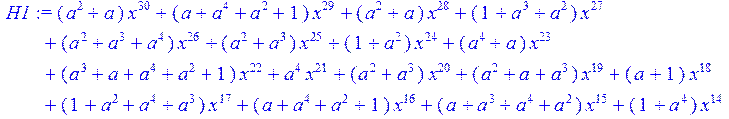
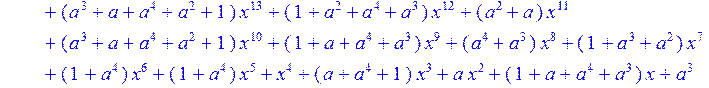
>
> for i from 0 to 30 do f[i]:=Rem (E,v[i],x)mod 2 od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>
> H12:=simplify((coeff(H1,x,0)*B[1]+coeff(H1,x,1)*B[2]+coeff(H1,x,2)*B[3]+coeff(H1,x,3)*B[4]+coeff(H1,x,4)*B[5]+coeff(H1,x,5)*B[6]+coeff(H1,x,6)*B[7]+coeff(H1,x,7)*B[8]+coeff(H1,x,8)*B[9]+coeff(H1,x,9)*B[10]+coeff(H1,x,10)*B[11]+coeff(H1,x,11)*B[12]+coeff(H1,x,12)*B[13]+coeff(H1,x,13)*B[14]+coeff(H1,x,14)*B[15]+coeff(H1,x,15)*B[16]+coeff(H1,x,16)*B[17]+coeff(H1,x,17)*B[18]+coeff(H1,x,18)*B[19]+coeff(H1,x,19)*B[20]+coeff(H1,x,20)*B[21]+coeff(H1,x,21)*B[22]+coeff(H1,x,22)*B[23]+coeff(H1,x,23)*B[24]+coeff(H1,x,24)*B[25]+coeff(H1,x,25)*B[26]+coeff(H1,x,26)*B[27]+coeff(H1,x,27)*B[28]+coeff(H1,x,28)*B[29]+coeff(H1,x,29)*B[30]+coeff(H1,x,30)*B[0])mod 2);
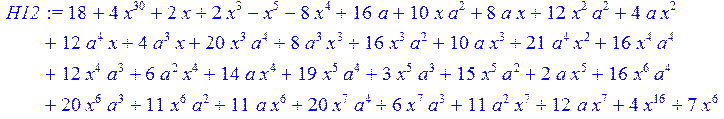
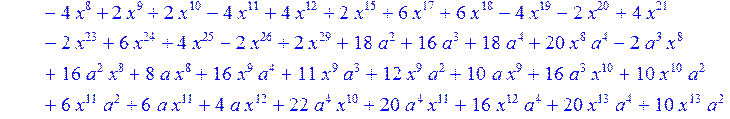
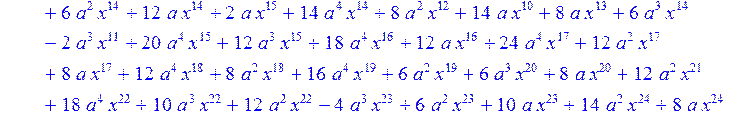
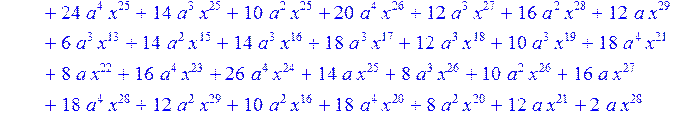
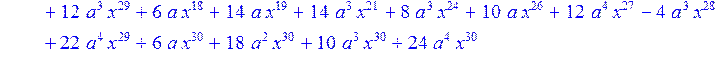
> H13:=simplify (H12)mod 2;
![]()
> c123:=b-H13;
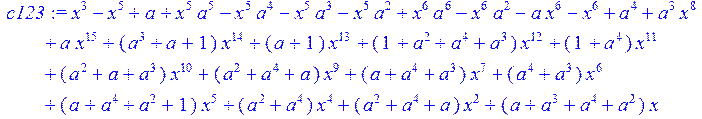
> A:=simplify (c123)mod 2;

> A1:=sort(collect(A,x)mod 2);
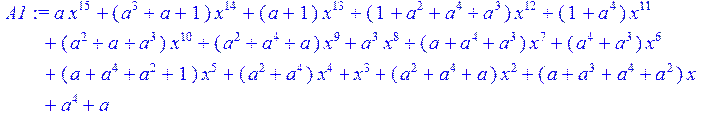
> c3;
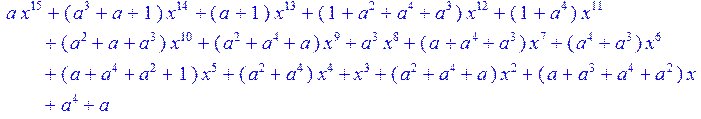
Результатом выполнения данной курсовой работы является разработанная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.