Поиск таблицы истинности для каждой БФ, реализующей заданную подстановку, страница 3

X1	X2	X3	Y
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Алгебраическая степень нелинейности: 3

7. Для БФ f(x₁, x₂, x₃)= x₁ x₂ Å x₂ x₃ Å x₃ определить таблицу истинности и корреляционную эффективность.

X1	X2	X3	Y
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

8. Нарисовать схему регистра сдвига, соответствующего многочлену x³+x²+1. Определить состояние регистра сдвига с начального состояния 0100 вплоть до возвращения в начальное состояние.

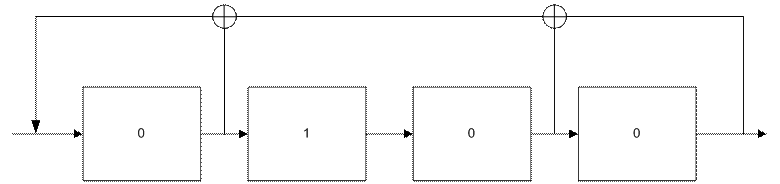
Состояния регистра:

0100

0010

1001

0100

9. Определить параметры генератора М-последовательности, соответствующие многочлену x⁴+x³+1.

10. Нарисовать схему регистра сдвига, соответствующую многочлену x⁵+x³+x+1. Определить его основные параметры.

11. Вычислить функцию Эйлера для чисел N = 567 и N = 1024.

j(587)=587-1 = 586

j(1024)=2¹⁰-2⁹ = 512

12. Найти все квадратичные вычеты по модулю чисел 11 и 19.

Для 11 – это 1, 3, 4, 5, 9

1² = 1

2² = 4

3² = 9

4² = 16 = 5

5² = 25 = 3

6² = 36 = 3

7² = 49 = 5

8² = 64 = 9

9² = 81 = 4

10² = 100 = 1

Для 19 – это 1,4,5,6,7,9,11,16,17

1² = 1

2² = 4

3³ = 9

4² = 16

5² = 25 = 6

6² = 36 = 17

7² = 49 = 11

8² = 64 = 7

9² = 81 = 5

10² = 100 = 5

11² = 121 = 7

12² = 144 = 11

13² = 169 = 17

14² = 196 = 6

15² = 225 = 16

16² = 256 = 9

17² = 4

18² = 1

13. Вычислить функцию Эйлера для чисел N = 213 и N = 2025.

j(213)=j(3*71) = 2 * 70 = 140

j(2025)=j(45²) = 2025 – 45 = 1980

14. Вычислить a/b mod p для значений

А) a = 79 b = 11 p = 97

Б) a = 5 b = 17 p = 131

79/11 = 79 * 53 = 4187 = 16

5/17 = 5 * 54 = 8

15.  Вычислить a^b mod p для значений

А) a = 13 b = 17 p = 131

Б) a = 5 b = 17 p = 131

13¹⁷ = 5

5¹⁷ = 4

16. Вычислить a^b mod p для значений

А) a = 7 b = 20 p = 109

Б) a = 38 b = 77 p = 47

7²⁰ = 25

38⁷⁷ = 15

17. Вычислить a/b mod p для значений

А) a = 79 b = 11 p = 97

Б) a = 5 b = 17 p = 131

По алгоритму Евклида

79/11 = x mod 97

79 = 11x mod 97

79*53 = x mod 97

x = 16

5/17 = x mod 131

5 = 17x mod 131

5*54 = x mod 131

x = 8

18. Вычислить a/b mod p для значений

А) a = 6 b = 18 p = 127

Б) a = 8 b = 24 p = 107

По алгоритму Евклида

6/18 = x mod 127

6 = 18x mod 127

6*120 = x mod 127

x = 85

8/24 = x mod 107

8 = 24x mod 107

8*58 = x mod 107

x = 36

19. Вычислить закрытый ключ d для криптосистемы RSA для открытого ключа e = 97 и значений модуля n = 299 и 527.

j(299) = (13-1)(23-1)=12*22=264

j(527) = (17-1)(31-1)=16*30=480

d97 = 1 mod 264

d = 49 mod 264

d97 = 1 mod 480

d = 193 mod 480

20. Вычислить закрытый ключ d и открытый ключ e для значений модуля n = 187 и 319.

j(187) = (11-1)(17-1)=10*16=160

j(319) = (11-1)(29-1)=10*28=280

de = 1 mod 160

пусть e = 17

17d = 1 mod 160

d = 113 mod 160

de = 1 mod 280

пусть e = 17

17d = 1 mod 280

d = 33 mod 280

21. Сформировать (n,t)-пороговую схему разделения секрета для следующих параметров p = 101, n = 7, t = 4.

Общий вид F(x) = a₃x³ + a₂x²+a₁x+a₀, все aÎGF(p),

a₀ – секрет, степень F(x) равна t-1.

Пусть F(x) = x³+13x²+4x+20

Найдем значения F(x) от произвольных n переменных :

y₁ = F(4) = 4³+13*4²+4*4+20 = 5 (mod 101)

y₂ = F(40) = 40³+13*40²+4*40+20 = 39 (mod 101)

y₃ = F(15) = 15³+13*15²+4*15+20 = 17 (mod 101)

y₄ = F(10) = 10³+13*10²+4*10+20 = 37 (mod 101)

y₅ = F(17) = 17³+13*17²+4*17+20 = 72 (mod 101)

y₆ = F(30) = 30³+13*30²+4*30+20 = 56 (mod 101)

y₇ = F(50) = 17³+13*17²+4*17+20 = 73 (mod 101)

F(x) = SL_i(x)y_i для всех i

L_i(x) = P(x-x_j)(x_i-x_j) для всех j¹i

Пусть восстановление идет по y₁, y₂, y₃, y₄

L₁(x) = (x-40)/(4-40)*(x-15)/(4-15)*(x-10)/(4-10)   =

L₂(x) = (x-4)/(40-4)*(x-15)/(40-15)*(x-10)/(40-10) =

L₃(x) = (x-4)/(15-4)*(x-40)/(15-40)*(x-10)/(15-10) =

L₄(x) = (x-4)/(10-4)*(x-40)/(10-40)*(x-15)/(10-15) =

F(x)= 5*L₁(x) + 39L₂(x)+ 17L₃(x)+ 37L₄(x)