Основные теоремы о дифференцируемых функциях

9. ОСНОВНЫЕ ТЕОРЕМЫ

 О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Эти важнейшие в математическом анализе теоремы связаны с име-нами знаменитых французских математиков:  П.Ферма (1601–1665), М.Ролль (1659–1719), Ж.Лагранж (1736–1813), О.Коши (1789–1857), Г.Ф.А.Лопиталь (1661–1704).

9.1. ТЕОРЕМЫ О НУЛЯХ ПРОИЗВОДНЫХ

9.1.1. Теорема Ферма. Пусть функция  определена на промежутке (a, b) и в его внутренней точке c, cÎ(a, b), принимает наибольшее или наименьшее значение. Тогда если производная в этой точке существует, то она равна нулю:

      Доказательство. Пусть в точке x = c, c Î (a, b), функция  принимает наибольшее значение. Выберем окрестность U(c) точки с такую, что U(c) Ì (a, b). Рассмотрим произвольное  приращение аргумента  Dx  в точке  c такое, что  с + Dx Î U(c). Соответствующее приращение функции  не положительно:

.

      Знак отношения приращений зависит от знака  Dx:

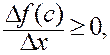 если  Dx < 0,

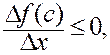 если Dx > 0.

      Поэтому  возможно одно из двух (теорема о предельном переходе в неравенстве):

1)  если предел отношения существует, то он равен нулю:

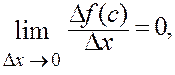
     т.е.

2)  предела  не существует,  т.е. в точке с не существует конечной производной.

      Аналогично рассматривается случай, когда в точке x = cфункция принимает наименьшее значение.

Геометрический смысл теоремы Ферма

      При выполнении условий теоремы Ферма касательная к графику функции в точке  параллельна оси абсцисс.

9.1.2. Теорема Ролля.  Пусть функция   удовлетворяет условиям:

1)  непрерывна на отрезке [a, b];

2)  дифференцируема во всех внутренних точках  x Î (a, b);

3)  на границах отрезка принимает равные значения

.

Тогда существует такая внутренняя точка отрезка  x = c, c Î (a, b), в которой .

      Доказательство. Из непрерывности функции    на отрезке [a, b]  следует (гл. 7, вторая теорема Вейерштрасса), что она на этом отрезке в точках  x₁, x₂достигает своего наименьшего  m = f(x₁) и наибольшего M = f(x₂) значения. Возможны два следующих случая.

        1) m = M.Это означает, что функция    на отрезке [a, b] сохраняет постоянное значение и, следовательно, производная равна нулю во всех внутренних точках отрезка.

    2) m < M. Из третьего условия теоремы следует, что в этом случае, по крайней мере, одна из точек  x₁  или  x₂  – внутренняя точка отрезка  [a, b]. В соответствии с теоремой Ферма эта точка и будет нулем производной.

Геометрический смысл теоремы Ролля  (рис.9)

      При выполнении условий теоремы Ролля на графике функции существует точка, в которой касательная к графику параллельна оси абсцисс.

                        Рис. 9

Механический смысл теоремы   Ролля

      Если функция , удовлетворяющая условиям теоремы Ролля, определяет зависимость координаты движущейся точки от времени,  то  на  интервале времени (a, b) скорость движения хотя бы один раз обратится в нуль.

      Сохраняя историческую достоверность, отметим, что  Ролль доказал теорему для случая, когда функция  – многочлен и . В такой постановке теорему можно сформулировать так: между двумя нулями многочлена существует нуль его производной. В дальнейшем не представило большого труда обобщить теорему на функцию, удовлетворяющую условиям 1, 2, 3, произвольного вида.

      Из доказанной теоремы легко получить следующее утверждение, которое является частным случаем теоремы Ролля.

      Следствие. Между двумя нулями дифференцируемой функции лежит хотя бы один нуль ее производной.

      П р и м е р  1. Функция , , удовлетворяет условиям теоремы Ролля.  Производная  равна нулю в точке  c = p/2.

      П р и м е р  2.  Квадратный трехчлен  ,    имеет два корня: a = –3   и   b = 1.  Производная   имеет корень  c = –1.

9.2. ТЕОРЕМА ЛАГРАНЖА

 И ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ

9.2.1. Теорема Лагранжа.  Пусть функция  удовлетворяет следующим условиям:

1)  непрерывна на отрезке   [a, b];

2)   дифференцируема во всех внутренних точках  x Î (a, b).

Тогда существует такая точка c, cÎ(a, b), для которой справедлива формула:

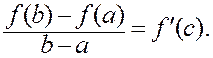                              (9.2.1)

      Доказательство. Рассмотрим функцию

                       (9.2.2)

где Q – постоянная, которую мы выберем так, чтобы для этой функции выполнялись условия теоремы Ролля.

      Ясно, что условия 1 и 2 выполнены, выполнение условия 3 () обеспечиваем соответствующим выбором постоянной Q.   поэтому, полагая , получаем

.

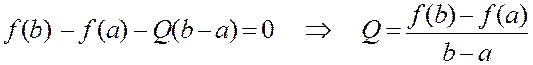Для функции

             (9.2.3)

в силу  теоремы Ролля существует такая точка  x = c,  c Î (a, b), в которой производная функции обращается в нуль: .

      Эту точку  x = c  “из теоремы Ролля” подставим в выражение для производной  функции  (9.2.3)

.

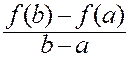Тогда 

   Þ  ,

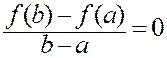откуда и получаем то, что требовалось доказать.

      Формула (9.2.1) называется   формулой Лагранжа.

Геометрический смысл теоремы Лагранжа

      На дуге графика функции, которая удовлетворяет условиям теоремы Лагранжа, существует точка, в которой касательная параллельна хорде, стягивающей концы дуги (рис. 10).

      Заметим, что теорема Ролля есть частный слу                      чай теоремы Лагранжа, когда . Тогда из формулы Лагранжа следует, что , а это и есть утверждение теоремы Ролля.

9.2.2. Формула конечных приращений. Предположим, что функция удовлетворяет условиям теоремы Лагранжа на некотором отрезке. Пусть в произвольной внутренней точке  x_оэтого отрезка имеем достаточно малое по абсолютной величине приращение аргумента Dx (такое, что  x_о + Dxне покидает упомянутого отрезка). Рассмотрим соответствующее  приращение функции

Df(x_о) = f(x_о+Dx) – f(x_о).

      В соответствии с теоремой Лагранжа между двумя точками  х_о и  x_о + Dxсуществует такая точка c, для которой справедлива формула Лагранжа:

.

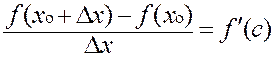Умножив на Dx,получаем формулу конечных приращений:

Df(x_о) =Dx,

где точка  с  лежит между точками  x_о  и  x_о + Dx.

       П р и м е р  3.  На дуге параболы  y = x²,  ,  найти точку, в которой касательная параллельна хорде, стягивающей концы этой дуги.

      Подставляя в формулу Лагранжа  a = 0, b = 2,  f(x) = x²,  находим точку c, в которой производная  f¢(x) = 2. Ясно, что с = 1, и  в  точке  параболы  С(1, 1)  касательная параллельна хорде.

9.3. ТЕОРЕМА КОШИ

      Приведем теперь следующую теорему, из которой, как частный случай, следует теорема Лагранжа.

      Теорема Коши. Пусть функции f(x)  и  g(x) удовлетворяют следующим условиям:

1)  непрерывны на отрезке [a, b];

2)  дифференцируемы в каждой точке интервала (a, b);

3)  .

Тогда существует точка c, cÎ(a, b), для которой справедлива формула

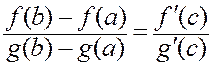.                           (9.3.1)

Эта формула называется  формулой Коши.

      Доказательство. Заметим, что из третьего условия теоремы следует, что  . В противном случае в силу теоремы Ролля нашлась бы точка, в которой производная  обращалась в нуль, что противоречит условию (3).

      Рассмотрим  функцию

,

в которой постоянную Q выберем так, чтобы эта функция удовлетворяла условиям теоремы Ролля. Речь идет о третьем условии теоремы, т.к. ясно, что два первых условия выполнены.

.

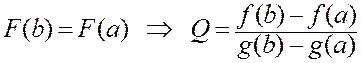Теперь в силу теоремы Ролля для функции

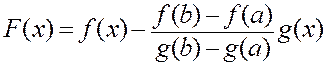
существует точка, c, cÎ(a, b), в которой ее производная равна нулю:

.

Определяем значение производной в этой точке и приравниваем его нулю.

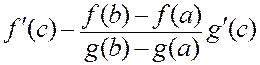 = 0,

отсюда и следует то, что требовалось доказать.