


ФОРМУЛА ТЕЙЛОРА
1. ПОСТАНОВКА ЗАДАЧИ
Если функция f(x) дифференцируема в точке хo, то она допускает в окрестности этой точки приближение в виде линейной функции с точностью до бесконечно малой о(х - хo):
f(x) = f(xо) + f¢(xо)(х - хo) + о(х - хo). (1)
Пример 1. Sinx = x + о(х).
Поставим задачу выбора приближения функции с точностью до БМФ более высокого порядка в классе многочленов в окрестности данной точки:
f(x) = Pn(x)+ о((х - хo)n). (2)
2. МНОГОЧЛЕН ТЕЙЛОРА
Предположим, что функция f(x) в точке хo имеет производные всех порядков до n-го включительно. Многочлен Pn(x) выберем так, чтобы выполнялись следующие условия:
f(xo) = Pn(xo),
f ¢(xo) = Pn¢(xo),
f²(xo) = Pn²(xo),
. . . . . . . . . . . .
f(n)(xo) = Pn(n)(xo). (3)
Иначе говоря, значения функции f(x) и ее производных до n-го порядка включительно должны быть равны соответствующим значениям многочлена Pn(x) и его производных.
Многочлен Pn(x) представим в виде
Pn(x) = ao + a1(х - хo) + a2(х - хo)2 + . . . + an(х - хo)n, (4)
т.е. расположим его по степеням х - хo.
Если в (4) подставить хo и воспользоваться первым из условий (3), то получим: ao = f(xo).
Дифференцируем (4), получаем
Pn¢(x) = a1 + 2a2(х - хo) + . . . + nan(х - хo)n. (5)
Подставляя теперь хo в (5) и пользуясь вторым из условий (3), по-лучаем: a1 = f ¢(xo).
Последовательно дифференцируя n раз, аналогично находим все коэффициенты многочлена (4):
ao = f(xo),
a1 = f ¢(xo),
a2 = ![]() f ²(xo), . . . , an =
f ²(xo), . . . , an =
![]() f (n)(xo).
(6)
f (n)(xo).
(6)
Многочлен (4), удовлетворяющий условиям (3), имеет коэффициенты (6):
Pn(x) = f(xo)
+ f ¢(xo)(х -
хo) + ![]() f²(xo)(х
- хo)2 + . . . +
f²(xo)(х
- хo)2 + . . . + ![]() f (n)(xo)(х - хo)n.
f (n)(xo)(х - хo)n.
Легко показать, что многочлен, удовлетворяющий условиям (3) единственный и имеет коэффициенты (6).
Этот многочлен называется многочленом Тейлора (1712, Brook Taylor, 1685-1731) а его частный случай, когда xo = 0, называется многочленом Маклорена (1742,Colin Maclauren, 1698-1746).
Многочлен Маклорена:
Pn(x) = f(0) + f ¢(0) х + ![]() f²(0) х2 + . . . +
f²(0) х2 + . . . + ![]() f (n)(0)
хn.
f (n)(0)
хn.
4. ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ФОРМЕ ПЕАНО
Теорема 1. Если функция f(x) в точке хo имеет производные всех порядков до n-го включительно, то справедлива формула
f(x) = Pn(x)+ о((х - хo)n), (7)
где Pn(x) – многочлен Тейлора, о((х - хo)n) – БМФ более высокого порядка, чем (х - хo)n в окрестности точки xo.
Доказательство. Докажем, что
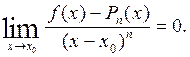
Применяя правило Лопиталя последовательно nраз, получаем то, что требовалось доказать.
Формула (7) называется формулой Тейлора с остаточным членом в форме Пеано (Giuseppe Peano, 1858-1932).
Пример 2. Sinx = x – x3/3! + о(х3).
5. ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ФОРМЕ ЛАГРАНЖА
Теорема 2. Если функция в окрестности точки xo имеет непрерывные производные до n + 1 порядка включительно, то справедлива формула
f(x)
= Pn(x)+ 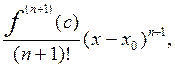 (8)
(8)
где Pn(x) – многочлен Тейлора, с – некоторая точка, лежащая между точками х и хo.
Доказательство. Обозначим
Rn(x) = f(x) – Pn(x).
Рассмотрим отношение двух функций
F(x) = Rn(x) и G(x) = (х - хo)n+1:
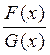 =
= 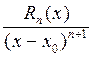 .
.
Эти функции удовлетворяют условиям теоремы Коши на отрезке [xo, x], xo<x, (или на отрезке [x, xо], если x< xо). Заметим при этом, что F(xо) = Rn(xо) = 0 и G(xо) = (хо - хo)n+1 = 0. По формуле Коши имеем:
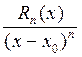 =
= 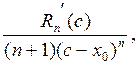
где с – точка (из теоремы Коши) между точками х и хo. Теперь применим теорему Коши к частному двух функций, стоящих в правой части последней формулы, для отрезка [xo, с], xo< с, (или для отрезка [с, xо], если с < xо). И так далее до получения формулы
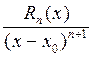 =
= 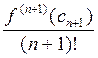 ,
,
откуда и получаем требуемое
Rn(x)
= 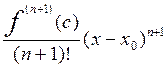 .
.
Формула (8) называется формулой Тейлора с остаточным членом в форме Лагранжа (Joseph Louis Lagrange, 1736-1813).
Пример 3. Sinx = x – x3/3! +x5/5! Cos с, где 0 < c < xили x<c<0. Здесь можно оценить точность при замене Sinxна приближенное значение x – x3/6: | Sinx – x – x3/3!| £ x5/120.
1712, Brook Taylor, 1685-1731
1742,Colin Maclauren, 1698-1746
Giuseppe Peano, 1858-1932
Joseph Louis Lagrange, 1736-1813
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.