S°a, S°в, S°с, S°d – стандартные абсолютные энтропии исходных веществ и продуктов реакции.
Стандартная энтропия индивидуальных веществ S°298 имеет размерность Дж/(моль·К) и характеризует количество теплоты, которое рассеивается в окружающую среду при нагревании 1 моля вещества на 1К.
Стандартное изменение энтропии химической реакции, протекающей при температуре, отличной от 298 К, вычисляется по уравнению
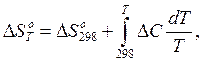 (11)
(11)
где ΔС – изменение теплоемкости в результате протекания реакции, которое выражается уравнением (8). В развернутом виде уравнение (11) имеет вид:
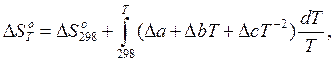
а после интегрирования становится удобным выражением для расчета изменения энтропии химической реакции при температуре Т:
ΔS°T = DS°298 +Da·ln![]() +Db·(T-298)-
+Db·(T-298)-![]() Dc·(T-2-298-2). (12)
Dc·(T-2-298-2). (12)
Для изолированной системы, как следует из второго закона термодинамики, знак изменения энтропии может являться критерием протекания самопроизвольного процесса в ней. На рисунке 3 представлена схема изменения состояния изолированной системы.
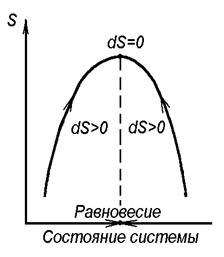
Рисунок 3. Направления изменения энтропии
в изолированной системе
Все самопроизвольные процессы, а других не может быть в изолированной системе по определению, будут происходить в направлениях, указанных стрелками, и будут сопровождаться повышением энтропии. Только в состоянии равновесия изменение энтропии равно нулю.
2.4. Изменение энергии Гиббса химической реакции
Критерием самопроизвольного протекания химической реакции в неизолированной физико-химической системе для изобарных условий является изменение энергии Гиббса реакции rGреак.. Изменение энергии Гиббса термодинамической системы выражается формулой:
rG = DH - Т ·DS, (13)
где DS– изменение энтропии, Т – абсолютная температура.
Самопроизвольное возрастание энтропии S, сопровождающее приближение системы к равновесию, характеризуется переходом энтальпии H из концентрированной формы - энергии Гиббса G, в рассеянную форму - Т·S. Энергия Гиббса является функцией состояния системы, определяющей величину той части энтальпии, которая еще не рассеялась и за счет которой система еще может совершать работу. Таким образом, в самопроизвольных процессах энергия Гиббса убывает (rG < 0) (рисунок 4). При достижении равновесия она принимает минимальное значение (G = Gmin), а ее приращение обращается в ноль (rG = 0).
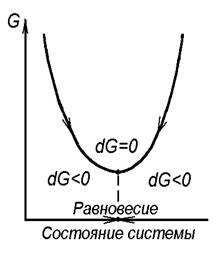
Рисунок 4. Направления изменения энергии Гиббса
в неизолированной системе
Для температуры 298 К в соответствие с уравнением (13) получим уравнение для расчета изменения энергии Гиббса химической реакции
rG°298 = DH°298 - 298 ·DS°298, (14)
для других температур rG°Т определяется аналогично.
Термодинамический анализ возможности протекания химической реакции в неизолированных системах в изотермических условиях, таким образом, состоит в определении величины и знака изменения энергии Гиббса реакции - rG°реак (рисунок 4). При rG°реак< 0 возможно самопроизвольное протекание реакции, при rG°реак= 0 реакция находится в состоянии равновесия, а при rG°реак > 0 самопроизвольное протекание реакции запрещено.В последнем случае возникает необходимость в оценке той температуры, при которой rG°реак= 0 и, выше которой rG°реак.< 0 , т.е. создается возможность самопроизвольного протекания реакции. Возможность такого расчета иллюстрируется схемой, представленной на рисунке 5, на которой показана типичная для большинства реакций линейная зависимость rG°реак. от температуры (13). Ее расчет проводится из выражения (13):
rG° = 0= DH°Т – Тнач.реакции ·DS°Т, откуда получаем
Тнач.реакции = DHТ/DSТ. (15)
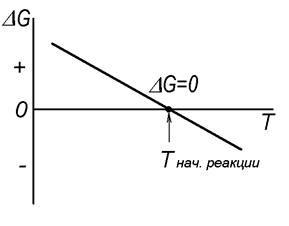
Рисунок 5. Схема определения температуры начала реакции
Как видно из рисунка 5 температуру, при которой rG°реак= 0 называют температурой начала реакции – Тнач.реакции, несмотря на то, что при этой температуре никакая химическая реакция невозможна. Для ее реального протекания необходимо rG°реак.< 0, но особый физический смысл этой температуры очевиден.
2.5. Расчет константы равновесия химической реакции
Достижение в физико-химической системе термодинамического равновесия характеризуется, в частности, состоянием химического равновесия, когда скорость прямой реакции равна скорости обратной реакции. Поэтому для процесса аА + bВ Û eE + dD, протекающего при Р и Т = constбудут неизменными и отношения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.