Промышленные запасы в зоне вытеснения.
а) Полоса.
![]()
 |
б) Для круговой залежи.

Схема многорядной системы залежи для полосовой и круговой залежи.
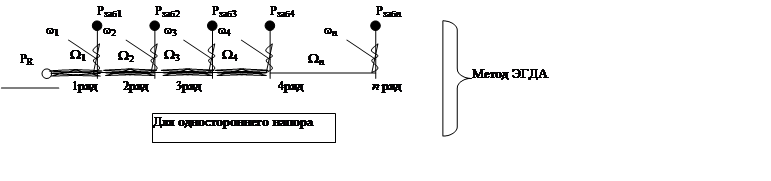 |
Рассмотрим двухсторонний напор:
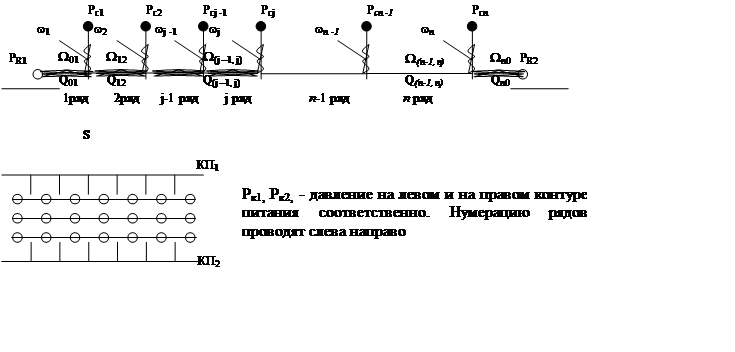 |
wj – внутреннее сопротивление j-ряда;
Wj-1, j – общее обозначение внешних сопротивлений зоны между рядом с индексом j-1 и j;
Wn0 – внешнее сопротивление зоны между n-рядом и правым контуром питания;
Qj-1, j – расход жидкости в зоне между рядом с индексом j-1 и j;
Qn0 – расход жидкости в зоне между n-рядом и правым контуром питания;
Для первого ряда при j = 1 w0 = 0, и Рк1 = Рс0:
![]()
Придавая индексу j последовательно значения от 1 до n, где n – количество рядов, получим систему n – уравнений. К этой системе необходимо присоединить еще одно уравнение для зоны между n – рядом и правым контуром питания Рк2:
![]()
Уравнение интерференции для двухстороннего напора.
При двухстороннем напоре вся область течения между двумя контурами питания разбивается на две зоны. В этих зонах, в какой-то определенный момент времени, течения между двумя рядами скважин будут противоположны по направлению. Границей этих двух зон обычно будет какой-нибудь из внутренних рядов скважин. Приток жидкости к этому ряду будет двухсторонним в отличие от других рядов, приток к которым только односторонний. Такой ряд скважин называется потокообразным. Какой из действующих рядов является потоко-радиальным неизвестно, и подлежит определению. Но в общем виде положение потокообразного ряда зависит от соотношения давления на контурах питания и на забое скважин, а также от величины андродинамических сопротивлений в данный момент времени. В процессе разработки залежи положение потокообразного ряда может изменяться.
Система уравнений которая составляется исходя из общей интерференции рядов составляется по знакам так, как если бы течение происходило бы слева направо. Это было бы возможно, если бы давление на линии n – ряда было бы больше, чем давление на правом контуре питания, но так, как обычно давление на контуре питания больше Рср на линии n – ряда, то часть значений Q получится с отрицательным знаком, а это означает, что на соответствующем участке течение направлено справа налево, а не наоборот, как мы задавались ранее. В этом случае потокообразным рядом будет тот ряд, для которого значения Q имеют слева положительные, а справа отрицательные знаки. Дебит j – ряда Qj получается как алгебраическая разность двух расходов соседних с этим рядом зон, сохраняя их знаки, получаемые при решении системы.
Метод эквивалентных сопротивлений.
Если делать гидродинамические расчеты для залежи, все скважины которой имеют одинаковые забойные давления, то левые части уравнения интерференции рядов обращаются в ноль (исключая составленное уравнение первого ряда). Это позволяет последовательно определить дебиты последующих рядов от дебита предыдущих. Для решения таких задач и создан метод эквивалентных сопротивлений. По этому методу сначала находят эквивалентное внутреннее сопротивление некоторой фиктивной галереи, стоящей на месте действительного первого ряда скважин. Это эквивалентное внутреннее сопротивление равно сопротивлению всей сложной системы внутренних и внешних сопротивлений всех действующих рядов (кроме первого) и внутренних сопротивлений всех действующих рядов.
Для расчета используют метод электрогидродинамической аналогии. При использовании этого метода, предварительно нарисовав расчетную схему рядов и складывая: 1. сопротивление при их последовательном включении и 2. проводимости при их параллельном включении, причем начиная расчеты с внутренних сопротивлений последнего ряда мы придем к выражению, эквивалентного сопротивления галереи в виде многократной дроби.
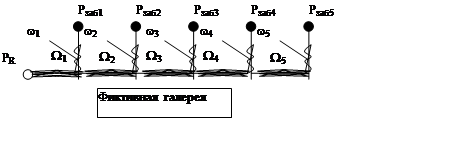 |
1. Сопротивления w5 и W5 включены последовательно, следовательно их общее сопротивление: w5 + W5.
2. Общее сопротивление w5 + W5 включено параллельно внутреннему сопротивлению четвертого ряда, следовательно их общее сопротивление:
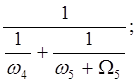
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.