В случае нормального распределения следует ожидать, что примерно 95% всех данных окажутся в пределах двух величин стандартного отклонения от среднего значения. Этот факт будет иметь большое значение при рассмотрении статистических выводов, поскольку допустимые погрешности оценок часто ограничиваются величиной 5%.
И, наконец, мы вправе предположить, что почти все данные (99,7%) будут находиться в пределах трех величин стандартного отклонения от среднего значения. При этом только 0,3% всех значений набора данных оказываются от среднего на большем удалении. На рисунке можно видеть, что график нормального распределения на расстояниях порядка трех стандартных отклонений от среднего опускается почти до нуля.
В картах контроля, которые широко используют для контроля качества продукции, пределы часто устанавливаются таким образом, чтобы в качестве заслуживающей внимания проблемы выступали именно те результаты наблюдений, которые отстоят от среднего на расстоянии, большем чем три стандартных отклонения.
В случае идеального нормального распределения в точности 95% всех данных попадают в область вблизи среднего значения в пределах 1,96 стандартного отклонения. Поскольку величина 1,96 достаточно близка к значению 2, мы используем описание "две величины стандартного отклонения" в качестве удобного и хорошего приближения.
Что же происходит в том случае, если набор данных не подчиняется нормальному распределению? В таком случае описанные выше проценты применять нельзя. К сожалению, поскольку существует множество скошенных (или других, отличающихся от нормального) распределений, нельзя указать единое правило определения таких процентов для произвольного распределения.
Существует, однако, ограничение, которое называется правилом Чебышева. В соответствии с этим правилом, по меньшей мере 1 - 1/а2 значений попадает в промежуток, лежащий в пределах а стандартных отклонений от среднего значения. Например, при а = 2 по меньшей мере 75% данных (это значение рассчитывается как 1 - 1/а2) должно находиться не далее, чем на расстоянии удвоенного стандартного отклонения от среднего, даже если распределение не является нормальным (сравните с величиной для нормального распределения, составляющей примерно 95%). Если а = 3, по меньшей мере 88,9% данных будет находиться в пределах утроенного стандартного отклонения от среднего значения.
Пример. Контрольные карты
Карта контроля содержит результаты отдельных измерений, средние значения (которые, как можно видеть, проходят через центр данных) и контрольные границы (которые устанавливаются выше и ниже среднего значения на расстоянии трех стандартных отклонений). На рисунке показан пример карты контроля качества.
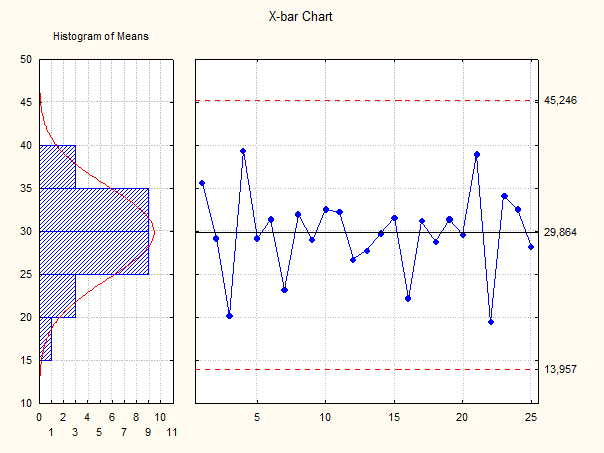
Показаны линии нижней и верхней контрольных границ, среднее значение, которое проходит через центр данных. Система находится под контролем, и есть только случайные отклонения от среднего, поскольку в отклонениях нет четких тенденций и результатов измерений, которые выходят за пределы контрольных границ. Карты контроля качества помогают выявить проблему. Дальнейшее исследование и исправление ситуации зависит от менеджера.
Стандартное отклонение выборки и генеральной совокупности
Существуют два различных (однако связанных между собой) вида стандартного отклонения: стандартное отклонение выборки (для выборки, сделанной из большей генеральной совокупности, обозначается буквой S) и стандартное отклонение генеральной совокупности (для всей генеральной совокупности, обозначается буквой s — малая греческая буква "сигма").
Названия этих величин отражают правила их использования. В случае работы с выборкой данных, взятых случайным образом из большей генеральной совокупности, используется стандартное отклонение выборки. Если же изучается вся генеральная совокупность, следует использовать стандартное отклонение генеральной совокупности (часто также используют термины "выборочное стандартное отклонение" и "генеральное стандартное отклонение" соответственно).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.