Изменчивость: изучение разнообразия. Стандартное отклонение: традиционный выбор. Размах: быстрая и поверхностная оценка, страница 3

Вычисление стандартного отклонения для выборки

Для того чтобы найти стандартное отклонение для выборки, необходимо вы­полнить следующие действия.

1. Найти отклонения, вычитая из каждого значения среднее.

2. Возвести полученные значения в квадрат, сложить и разделить полученную сумму на n - 1. Резуль­татом будет дисперсия.

3. Извлечь из полученного значения квадратный корень. Это и будет стандартное отклонение.

Формула для вычисления стандартного отклонения является краткой мате­матической записью описанной выше процедуры. Стандартное отклонение для выборки данных обозначается буквой S, и формулы вычисления стандартного отклонения и дисперсии имеют следующий вид.

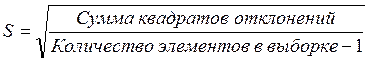
или

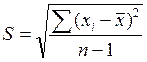
Стандартное отклонение имеет простую и понятную интерпретацию: эта ве­личина описывает типичное расстояние от среднего значения для отдельных значений набора данных. Таким образом, стандартное отклонение выступает в качестве меры изменчивости для этих отдельных значений. Поскольку стан­дартное отклонение отражает типичную величину отклонения, то можно пред­положить, что для одних значений отклонение будет меньше стандартного, а для других — больше.

Пример. Учет различий между клиентами

Ваши клиенты отличаются друг от друга; между ними существуют различия в размерах заказов, предпоч­тении различных товаров, цикличности работы в течение года, потребности в информации, привержен­ности работе с вами и т.п. Однако у вас, видимо, есть определенное суждение о "типичном клиенте", а также некоторое представление о степени различий между клиентами.

Вы можете обобщить информацию о заявках клиентов с помощью среднего и стандартного отклонения.

Таким образом, за последний год каждый клиент в среднем заказал товаров на сумму $85600. В качест­ве характеристики различий между клиентами выступает стандартное отклонение. Его величина в $28300 показывает, что обычно ваши клиенты делали заказы на суммы, меньшие или большие примерно на $28300, чем среднее значение в $85600. Слово "примерно" имеет здесь большое значение: некото­рые клиенты могут делать заказы, размер которых очень близок к среднему уровню, в то время как для других будут наблюдаться отличия, значительно превышающие $28300. Среднее значение показывает типичный объем поступивших в течение года заказов от одного клиента, а стандартное отклонение иллю­стрирует типичное отклонение от среднего.

Обратите внимание также на то, что стандартное отклонение измеряется в тех же единицах, что и сред­нее значение; в данном случае обе эти величины определены в долларах. Если говорить точнее, то еди­ница измерения здесь — это "доллар в год на одного клиента". Это увязывает единицы измерения с ис­ходным набором данных, который представляет собой последовательность объемов "долларов в год", причем каждому клиенту соответствует одно число.

Интерпретация стандартного отклонения для нормального распределения

В том случае, когда набор данных имеет приблизительно нормальное распреде­ление, стандартное отклонение приобретает особый смысл. Приблизительно две трети значений из такого набора данных находятся в пределах одного стандарт­ного отклонения по обе стороны от среднего значения. Около 95% всех значений нахо­дятся в пределах двух стандартных отклонений от среднего. И, наконец, мы можем ожидать, что обнаружим почти все данные (99,7%) на расстоянии не более трех стандартных отклонений от среднего.

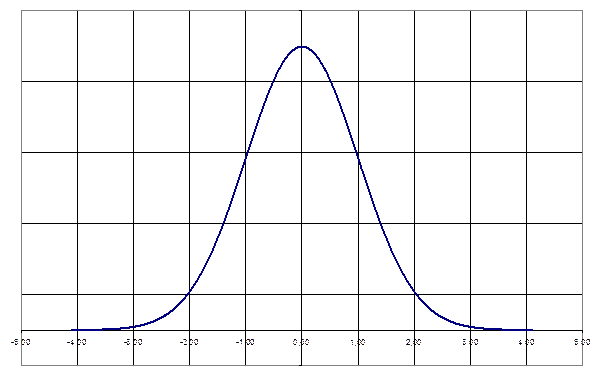
Так, например, если способности ваших работников распределены приблизи­тельно нормально, то вы можете ожидать, что оценки способностей примерно двух третей из них попадают на расстояния не более одной величины стандарт­ного отклонения от среднего значения — либо выше, либо ниже среднего. Это означает, что приблизительно треть работников имеет способности, лежащие в пределах одной величины стандартного отклонения выше среднего, а примерно треть — в соответствующей области ниже среднего. Остальные работники, кото­рых также приблизительно треть, распределятся таким образом: около полови­ны этой одной трети (шестая часть всех работников) обладает способностями, превышающими средние более чем на величину одного стандартного отклонения, и примерно шестая часть всех работников (увы!) окажется ниже среднего далее, чем на расстоянии одного стандартного отклонения.