Детали машин и основы конструирования. Часть 2: Методические указания по решению задач (Раздел «Механические передачи»)

Министерство образования Российской Федерации

_____

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ

В.И. КОРНИЛОВ, А.П. ТЮРИН

ДЕТАЛИ МАШИН И ОСНОВЫ КОНСТРУИРОВАНИЯ

Часть 2

Методические указания по решению задач

Санкт-Петербург

Издательство СПбГПУ

2008

УДК 621.81 (075.8)

        Корнилов В.И., Тюрин А.П. Детали машин и основы конструирования. Часть 2. Методические указания по решению задач. СПб.: Изд-во СПбГПУ, 2008.

Пособие соответствует Государственному образовательному стандарту дисциплины «Детали машин и основы конструирования» (ОПД.Ф.02.03), направления бакалаврской подготовки 551800 « Технологические машины и оборудование» и 552900 «Технология оборудования и автоматизация машиностроительных производств» (ОПД.Ф.05).

        Во второй части методических указаний рассматриваются задачи и примеры решения задач по разделу курса: «Механические передачи».

Пособие предназначено для подготовки студентов третьего курса механико-машиностроительного факультета к экзамену по дисциплине «Детали машин и основы конструирования».

Ил.  Библ.:  назв.

Рецензенты:

3. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ

3.1. Определить теоретическую толщину зуба по делительной окружности прямозубого цилиндрического колеса, выполненного со смещением, если модуль m = 6 мм, коэффициент смещения x = -0,5, угол профиля инструмента a = 20⁰.

Решение. Толщина зуба теоретического контура производящей рейки по делительной прямой, равна ширине впадины.   В станочном зацеплении шаг зубьев по начальной окружности нарезаемого колеса равен шагу зубьев производящей рейки.

.

По данной причине начальная окружность в станочном зацеплении называется делительной окружности колеса. При отсутствии смещения (коэффициент смещения x = 0) начальная и делительная прямые производящей рейки совпадают. В этом случае теоретическая толщина зуба нарезаемого колеса s по делительной окружности равна ширине впадины.

.

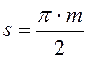        Для колеса, выполненного со смещением, из решения прямоугольного треугольника ABC получим

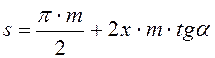, где

a = 20⁰ - угол профиля инструмента (производящей рейки)

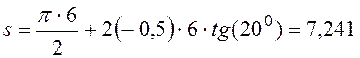мм.

Ответ. s = 7,241 мм.

3.2. При каком минимальном числе зубьев z прямозубого цилиндрического колеса, выполненного стандартным реечным инструментом без смещения (коэффициент смещения x = 0), диаметр основной окружности d_b меньше диаметра окружности впадин d_f?

Ответ. При z = 42.

3.3. Определить угол зацепления прямозубой цилиндрической передачи a_w, если передаточное число u = 3, диаметр основной окружности d_b2 = 162 мм, а межосевое расстояние равно a_w = 240 мм. (360)

Ответ. a_w = 25,84193⁰ (точность определения угловых размеров при геометрическом расчете передачи – не менее пяти значащих цифр после запятой).

        3.4. Составить расчетную схему и определить приведенный радиус кривизны r_ПР в полюсе зацепления прямозубой цилиндрической передачи.         Принять следующие исходные данные: межосевое расстояние a_w = 70 мм, числа z₁ = 20, z₂ = 50, угол профиля инструмента a = 20^о, угол зацепления a_w = 28^о.

Ответ. r_ПР = 30,43 мм.

        3.5. Проверить выполнение условия плавности работы цилиндрической косозубой передачи  (e_b³ 1,1), если нормальный модуль зацепления m = 2,5 мм, ширина зубчатого венца шестерни b₁ = 34 мм, колеса b₂ = 30 мм,  угол наклона b = 17⁰.

Решение. Плавность работы цилиндрической косозубой передачи определяется условием

, где

        e_b – осевой коэффициент перекрытия;

        b_w– ширина зацепления, равная меньшему из двух значений b₁ и b₂.

        Желательно, чтобы осевой коэффициент перекрытия e_b или суммарный коэффициент перекрытия e_g = e_a + e_b был близок к целому числу. В этом случае суммарная длина линий контакта в зацеплении имеет постоянное значение для любой фазы зацепления.

.                                       

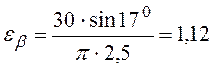Ответ. e_b = 1,12 ³ 1,1. Плавность работы передачи обеспечена.

3.6. Мощность на входном быстроходном валу двухступенчатого цилиндрического редуктора P₁ = 3500 Вт, частота вращения входного вала n₁ = 950 мин^-1.                                   

Определить вращающий момент T3 на выходном тихоходном валу редуктора, если z1 = 23, z2 = 75, z3 = 18, z4 = 51. При решении задачи задать недостающие данные.

Ответ. T₃ » 312 Нм.

3.7. Чугунный цилиндр 1 диаметром D = 250 мм и длиной L = 500 мм подвешен на двух тросах 2. Угол между тросами и вертикальной стальной стенкой a = 30^о.

Определить контактные напряжения sH, если плотность чугуна g1 = 7200 кг/м3, модуль упругости чугуна E1 = 0,8·105 МПа, стали E2 = 2,1·105 МПа.

        Решение. Контактные напряжения определяем по формуле Герца, которая для линейного контакта металлических цилиндров имеет вид

.

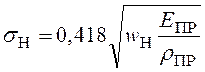        Здесь 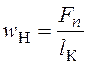, Н/мм – удельная нагрузка, как отношение нормальной силы в контакте F_n к длине линии контакта l_К;

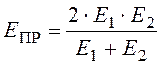        , МПа – приведенный модуль упругости;