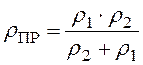 , мм – приведенный радиус кривизны для
внешнего контакта тел.
, мм – приведенный радиус кривизны для
внешнего контакта тел.
В рассматриваемом случае длина линии контакта lК = L;
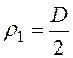 ,
, ![]() , следовательно
, следовательно
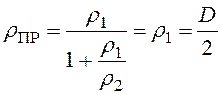 .
.
Величину нормальной силы Fn находим из решения треугольника сил. Равновесие цилиндра возможно, если результирующая сила Nот сложения сил Fn и G направлена вдоль натянутого троса.
![]() , Н, где
, Н, где
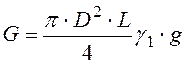 – вес цилиндра 1, Н.
– вес цилиндра 1, Н.
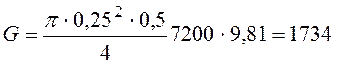 Н.
Н.
![]() Н.
Н.
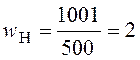 Н/мм.
Н/мм.
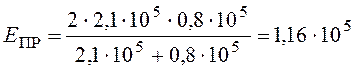 МПа.
МПа.
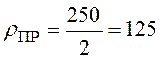 мм.
мм.
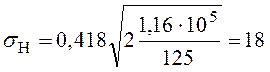 МПа.
МПа.
Ответ. sH = 18 МПа.
3.8. В прямозубых цилиндрической и реечной передачах диаметры делительных окружностей d всех колес одинаковы.
|
|
Во сколько раз контактные напряжения sH в конструкции а) меньше, чем в конструкции б) при одинаковых моментах на шестерне T1 и одинаковых материалах колес? |
Ответ. В ![]() раз меньше.
раз меньше.
3.9. В прямозубой цилиндрической передаче вращающий момент на шестерне T1 = 200 Нм, диаметр начальной окружности dw1 = 100 мм, ширина зацепления bw= 80 мм, угол зацепления aw = 200.
|
|
Нагрузка по ширине зубчатого венца распределена по
линейному закону Определить коэффициент kHb, используемой при расчете передачи на контактную прочность. |
Ответ. wHрасч = 66,5 Н/мм.
3.10. Определить коэффициент запаса контактной прочности sH колеса нереверсивной прямозубой цилиндрической передачи при регулярном режиме нагружения.
Принять следующие исходные данные: расчетные контактные напряжения в полюсе зацепления sH = 1200 МПа, частота вращения рассматриваемого колеса n= 100 мин-1, требуемый ресурс Lh = 500 ч, предел контактной выносливости sHlimb = 800 МПа, базовое число циклов NH0 = 6·107, показатель степени кривой выносливости m= 6.
Ответ. sH = 1,1.
3.11. Определить вращающий момент T1 на валу шестерни прямозубой цилиндрической передачи из условия контактной прочности, если известно, что диаметр начальной окружности dw1 = 100 мм, ширина зацепления bw= 60 мм, приведенный радиус кривизны при контакте в полюсе зацепления rПР = 12 мм, модуль упругости материала шестерни и колеса E = 2,1·105 МПа, угол зацепления aw = 200, коэффициент нагрузки KH = 1,2, допускаемые контактные напряжения [sH] = 400 МПа.
Ответ. T1 = 25,8 Н·м.
3.12. Определить допускаемые напряжения изгиба зубьев колеса нереверсивной прямозубой цилиндрической передачи при регулярном режиме нагружения.
Принять следующие исходные данные: требуемый ресурс Lh = 750 ч, частота вращения рассматриваемого колеса n = 20 мин-1, предел выносливости при изгибе зубьев sF lim b = 500 МПа, показатель степени кривой усталости m= 9, базовое число циклов NF0 = 4·106, допускаемый коэффициент запаса прочности [sF] = 1,75.
Ответ. [sF] = 337 МПа.
3.13. Проверить выполнение условия усталостной прочности в опасном сечении зуба прямозубого цилиндрического колеса.
|
|
Составляющие нормальной расчетной силы Fz = 16 кН и Fy = 10 кН, ширина зацепления bw = 40 мм, теоретический коэффициент концентрации напряжений в точках А и Б as = 1,6, допускаемые напряжения [sF] = 300 МПа. |
Решение. Расчет зуба прямозубого зубчатого колеса на усталостную прочность основывается на определении максимальных местных напряжений в опасном сечении зуба.
![]() .
.
Здесь
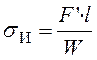 - напряжение изгиба;
- напряжение изгиба;
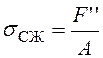 - напряжение сжатия;
- напряжение сжатия;
Геометрические характеристики опасного сечения:
![]() , мм2 - площадь;
, мм2 - площадь;
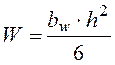 , мм3 – осевой момент
сопротивления.
, мм3 – осевой момент
сопротивления.
![]() мм2.
мм2.
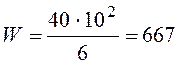 мм3.
мм3.
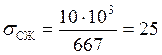 МПа.
МПа.
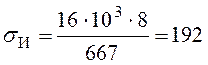 МПа.
МПа.
![]() МПа.
МПа.
Ответ. ![]() МПа.
МПа.
3.14. Составить схему сил, действующих в зацеплении косозубой цилиндрической передачи. Определить значения составляющих нормального усилия в зацеплении, если нормальный модуль m = 4 мм, число зубьев шестерни z1 = 23, колеса z2 = 50, x1 = x2 = 0, угол наклона b = 160, вращающий момент на валу колеса T2 = 500 Нм.
Потерями на трение допускается пренебречь.
Ответ. Окружная сила Ft1 = 5000 Н, осевая Fx1= 1434 Н, радиальная Fr1 = 1893 Н.
3.15. В одинаковую или в разную сторону следует назначать наклон зубьев на шестерне и колесе, расположенных на промежуточном валу двухступенчатого редуктора (см. рис. к задаче 3.7)?
Составить расчетную схему и обосновать ответ.
Ответ. Наклон зубьев шестерни и колеса для редуктора данного типа следует назначать в одинаковую сторону.
3.16. Составить схему сил, действующих в зацеплении прямозубой конической передачи. Определить значения составляющих нормального усилия в зацеплении, если диаметр средней делительной окружности колеса d2 = 200 мм, угол делительного конуса шестерни d1 = 300, колеса d2 = 900 - d1, угол зацепления aw = 200, вращающий момент на валу шестерни T1 = 200 Нм.
Ответ. Окружная сила Ft1 = Ft2 = 3464 Н, осевая Fx1 = Fr2= 630 Н, радиальная Fr1 = Fx2 = 1092 Н.
3.17. Определить коэффициент смещения инструмента xпри нарезании зубьев колеса червячной передачи, если передаточное число u= 15,5, осевой модуль m= 3 мм, межосевое расстояние aw = 63 мм, число заходов червяка z1 = 2, коэффициент диаметра червяка q = 12.
Ответ. x = -0,5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.