


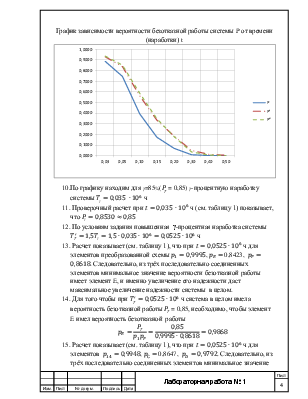





расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента, в качестве которого выберем элемент 6. Тогда
![]()
где ![]() - вероятность безотказной работы
мостиковой схемы при абсолютно надежном элементе 6;
- вероятность безотказной работы
мостиковой схемы при абсолютно надежном элементе 6; ![]() - вероятность безотказной работы
мостиковой схемы при отказавшем элементе 6.
- вероятность безотказной работы
мостиковой схемы при отказавшем элементе 6.
Учитывая, что ![]() , получим
, получим
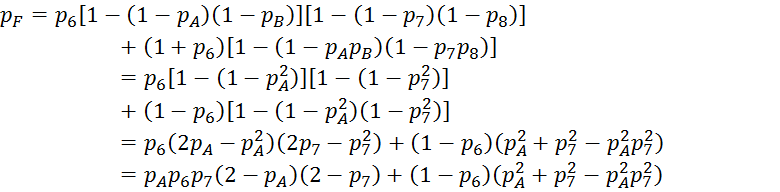
7. В преобразованной схеме элементы 1, C, D, F, 14 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы
![]()
8. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 14 подчиняется экспоненциальному закону
![]()
9. Результаты расчётов вероятностей безотказной работы элементов 1-14 исходной схемы для наработки 3·106 ч представлены в таблице
Таблица 1
Расчет вероятности безотказной работы системы
|
λ |
Наработка |
||||||||||
|
0,03 |
0,05 |
0,10 |
0,15 |
0,20 |
0,30 |
0,40 |
0,50 |
0,035 |
0,0525 |
||
|
1 |
0,01 |
0,9997 |
0,9995 |
0,9990 |
0,9985 |
0,9980 |
0,9970 |
0,9960 |
0,9950 |
0,9997 |
0,9995 |
|
2,3 |
1,00 |
0,9704 |
0,9512 |
0,9048 |
0,8607 |
0,8187 |
0,7408 |
0,6703 |
0,6065 |
0,9656 |
0,9489 |
|
4-8 |
5,00 |
0,8607 |
0,7788 |
0,6065 |
0,4724 |
0,3679 |
0,2231 |
0,1353 |
0,0821 |
0,8395 |
0,7691 |
|
9,10 |
0,20 |
0,9940 |
0,9900 |
0,9802 |
0,9704 |
0,9608 |
0,9418 |
0,9231 |
0,9048 |
0,9930 |
0,9896 |
|
11-13 |
5,00 |
0,8607 |
0,7788 |
0,6065 |
0,4724 |
0,3679 |
0,2231 |
0,1353 |
0,0821 |
0,8395 |
0,7691 |
|
14 |
0,10 |
0,9970 |
0,9950 |
0,9900 |
0,9851 |
0,9802 |
0,9704 |
0,9608 |
0,9512 |
0,9965 |
0,9948 |
|
A,B |
- |
0,8353 |
0,7408 |
0,5488 |
0,4066 |
0,3012 |
0,1653 |
0,0907 |
0,0498 |
0,8106 |
0,7298 |
|
C |
- |
0,9472 |
0,8749 |
0,6574 |
0,4586 |
0,3064 |
0,1271 |
0,0500 |
0,0191 |
0,9310 |
0,8647 |
|
D |
- |
0,9881 |
0,9802 |
0,9608 |
0,9418 |
0,9231 |
0,8869 |
0,8521 |
0,8187 |
0,9861 |
0,9792 |
|
F |
- |
0,9495 |
0,8729 |
0,6279 |
0,4063 |
0,2482 |
0,0857 |
0,0287 |
0,0097 |
0,9328 |
0,8618 |
|
E |
- |
0,9331 |
0,8533 |
0,6253 |
0,4255 |
0,2773 |
0,1094 |
0,0409 |
0,0149 |
0,9148 |
0,8423 |
|
P |
- |
0,8857 |
0,7444 |
0,3923 |
0,1726 |
0,0687 |
0,0093 |
0,0012 |
0,0001 |
0,8530 |
0,7255 |
|
11'-13' |
1,5882 |
0,9535 |
0,9237 |
0,8531 |
0,7880 |
0,7279 |
0,6210 |
0,5298 |
0,4520 |
0,9459 |
0,9200 |
График
зависимости вероятности безотказной работы системы P
от времени (наработки) t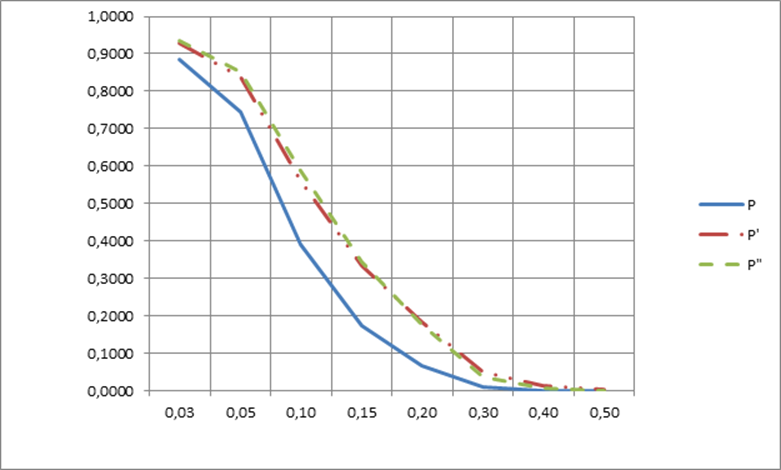
10.По графику находим для g=85%(![]() = 0,85) g-процентную наработку системы
= 0,85) g-процентную наработку системы ![]()
11.
Проверочный расчет при ![]() (см. таблицу 1) показывает, что
(см. таблицу 1) показывает, что ![]()
12.
По условиям задания повышенная g-процентная наработка
системы ![]()
13.
Расчет показывает (см. таблицу 1), что при ![]() для элементов преобразованной
схемы
для элементов преобразованной
схемы ![]() ,
, ![]() 0,8423,
0,8423, ![]() . Следовательно, из трёх
последовательно соединенных элементов минимальное значение вероятности
безотказной работы имеет элемент E, и именно увеличение его надежности даст максимальное увеличение
надежности системы в целом.
. Следовательно, из трёх
последовательно соединенных элементов минимальное значение вероятности
безотказной работы имеет элемент E, и именно увеличение его надежности даст максимальное увеличение
надежности системы в целом.
14. Для того чтобы при ![]() система в целом имела вероятность
безотказной работы
система в целом имела вероятность
безотказной работы ![]() = 0,85, необходимо, чтобы элемент E
имел
вероятность безотказной работы
= 0,85, необходимо, чтобы элемент E
имел
вероятность безотказной работы
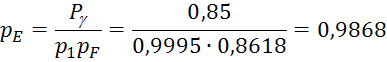
15.
Расчет
показывает (см. таблицу 1), что при ![]() для элементов
для элементов ![]() ,
, ![]() 0,8647,
0,8647, ![]() . Следовательно, из
трёх последовательно соединенных элементов минимальное значение вероятности
безотказной работы имеет элемент С, и именно увеличение его надежности даст
максимальное увеличение надежности элемента E и системы в целом.
. Следовательно, из
трёх последовательно соединенных элементов минимальное значение вероятности
безотказной работы имеет элемент С, и именно увеличение его надежности даст
максимальное увеличение надежности элемента E и системы в целом.
16.
Для того чтобы при ![]() элемент E
имел
вероятность безотказной работы
элемент E
имел
вероятность безотказной работы ![]() = 0,9868, необходимо, чтобы
элемент C
имел
вероятность безотказной работы
= 0,9868, необходимо, чтобы
элемент C
имел
вероятность безотказной работы
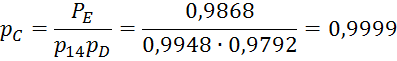
17. Для определения минимально необходимой вероятности безотказной работы элементов 11-13 используем графоаналитический метод.
18.
По графику видно, что при ![]() ,
, ![]()
19.
Так как по условиям задания все элементы работают в периоде нормальной
эксплуатации и подчиняются экспоненциальному закону, то для элементов 11-13
при ![]()
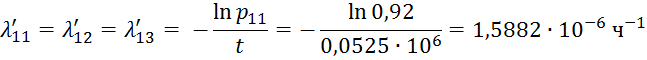
20.Таким
образом, для увеличения γ-процентной наработки системы надо увеличить
надежность элементов 11,12,13 и снизить интенсивность их отказов с 5,0 до
1,5882 ![]() , то есть в 3,14 раз.
, то есть в 3,14 раз.
21.
Результаты расчётов для системы с увеличеннойнадежностью элементов 11,12,13
приведены в таблице 1. Там же приведены расчетные значения ВБР системы «2 из 3»
С![]() и
системы в целом P
и
системы в целом P![]() .
При
.
При ![]() ВБР системы P
ВБР системы P![]() = 0,8237
= 0,8237
22.Для второго способа увеличения ВБР
системы – структурного резервирования – по тем же соображениям также выбираем
элемент C, ВБР которого после
резервирования должна быть не ниже ![]()
23.
Для элемента C системы «2 из 3»
резервирование означает увеличение общего числа элементов. Аналитически
определить минимально необходимое количество элементов невозможно, т. к. число
элементов должно быть целым и функция ![]() дискретна.
дискретна.
24.Для повышения надежности системы «2 из 3» добавляем к ней элементы, идентичные по надежности исходным элементам 11-13, до тех пор, пока ВБР квазиэлемента С не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом:
- добавляем элемент 15, получаем систему «2 из 4»:
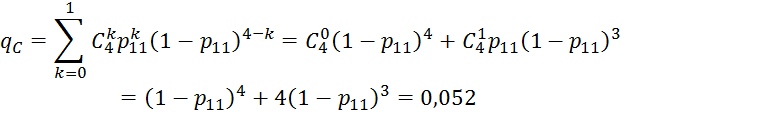
![]()
- добавляем элемент 16, получаем систему «2 из 5»:
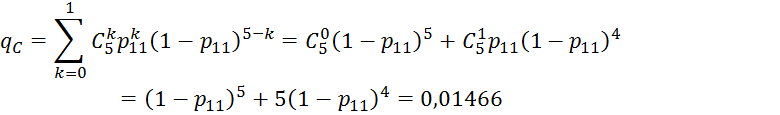
![]()
- добавляем элемент 17, получаем систему «2 из 6»:
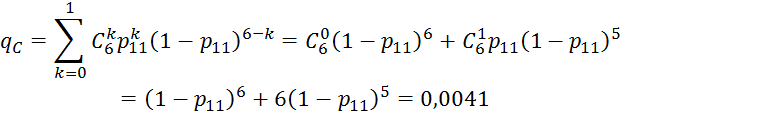
![]()
- добавляем элемент 18, получаем систему «2 из 7»:
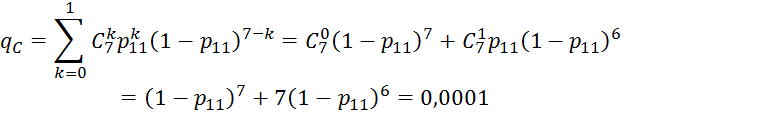
![]()
25.
![]() Таким образом, для
повышения надежности до требуемого уровня необходимо в исходной схеме систему
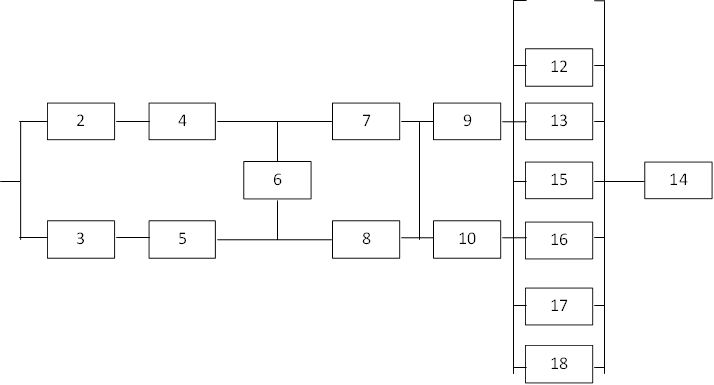
«2 из 3» достроить элементами 15, 16, 17, 18 до системы «2 из 7».
Таким образом, для
повышения надежности до требуемого уровня необходимо в исходной схеме систему
«2 из 3» достроить элементами 15, 16, 17, 18 до системы «2 из 7».
 |
|||
26.
Результаты расчетов ВБР системы «2 из 7» С![]() и
системы в целом P
и
системы в целом P![]() представлены
в таблице 1.
представлены
в таблице 1.
Лабораторная работа № 4
Критерии надежности восстанавливаемых изделий
Цель: Научиться рассчитывать критерии надежности восстанавливаемых изделий
|
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
t7 |
t8 |
tср |
tв |
закон распределения |
λ |
|
25 |
15 |
18 |
23 |
31 |
12 |
9 |
19 |
40 |
2,3 |
экспоненциальный |
3·10-5 |
1. Определить среднее время восстановления аппаратуры
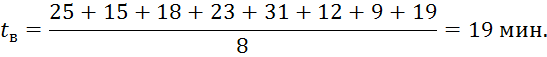
2. Определяем коэффициент готовности
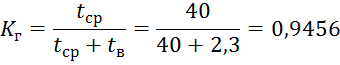
3. Определим количественные характеристики надежности элемента P(t), a(t), Tср, если t = 500, 1000 и 2000 часов
3.1 Для t = 500
![]()
![]()
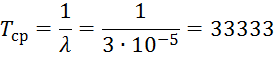
3.2 Для t = 1000
![]()
![]()
3.3 Для t = 2000
![]()
![]()
![]() Я научился рассчитывать критерии
восстанавливаемых изделий
Я научился рассчитывать критерии
восстанавливаемых изделий
Лабораторная работа № 5
Расчет характеристик надежности невосстанавливаемых резервированных изделий
Цель: Научиться рассчитывать критерии надежности невосстанавливаемых резервированных изделий технических систем
|
λ |
λ1 |
λ2 |
λ3 |
t |
|
5·10-5 |
2·10-3 |
2,5·10-3 |
3·10-3 |
300 |
1. Определяем наработку до первого отказа резервированного устройства
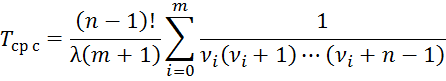
где ![]()
![]()
![]()
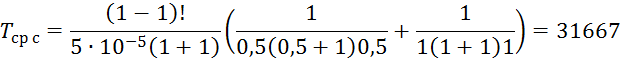
2. Определим вероятность безотказной работыизделия в течение времени
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.