









где:
![]() - число параметров уравнения регрессии
(число коэффициентов при объясняющей переменной х),
- число параметров уравнения регрессии
(число коэффициентов при объясняющей переменной х), ![]() -
объем совокупности.
-
объем совокупности.
 .
.
По таблице «F-распределения» находим
![]() .
.
Так
как ![]() , то необходимо принять гипотезу
, то необходимо принять гипотезу ![]() о случайной природе выявленной зависимости
и статистической незначимости параметров уравнения.
о случайной природе выявленной зависимости
и статистической незначимости параметров уравнения.
Рассчитаем средний коэффициент эластичности:
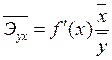 ;
;
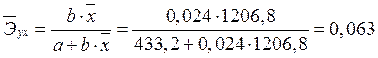 .
.
Оценивая коэффициент элачтичночти можно предположить, что с увеличением заработной платы и социальных выплат на 1%, потребительские расходы увеличатся на 0,063%.
Средняя
ошибка аппроксимации ![]() вышла за допустимые пределы
(8-10%), что говорит о неудачном выборе уравнения регрессии. Полученные оценки
параметров уравнения не позволяют использовать его для прогноза.
вышла за допустимые пределы
(8-10%), что говорит о неудачном выборе уравнения регрессии. Полученные оценки
параметров уравнения не позволяют использовать его для прогноза.
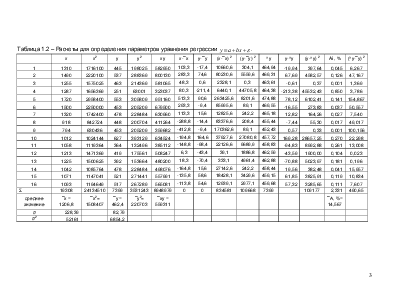
Таблица 1.2 –
Расчеты для определения параметров уравнения регрессии ![]() .
.
|
x |
x2 |
y |
y2 |
xy |
x-¯x |
y-¯y |
(x-¯x) 2 |
(y-¯y) 2 |
^y |
y-^y |
(y-^y) 2 |
Ai , % |
(^y-¯y) 2 |
|
|
1 |
1310 |
1716100 |
445 |
198025 |
582950 |
103,3 |
-17,4 |
10660,6 |
304,1 |
464,94 |
-19,94 |
397,64 |
0,045 |
6,267 |
|
2 |
1490 |
2220100 |
537 |
288369 |
800130 |
283,3 |
74,6 |
80230,6 |
5559,6 |
469,31 |
67,69 |
4582,57 |
0,126 |
47,167 |
|
3 |
1255 |
1575025 |
463 |
214369 |
581065 |
48,3 |
0,6 |
2328,1 |
0,3 |
463,61 |
-0,61 |
0,37 |
0,001 |
1,369 |
|
4 |
1287 |
1656369 |
251 |
63001 |
323037 |
80,3 |
-211,4 |
6440,1 |
44705,8 |
464,38 |
-213,38 |
45532,43 |
0,850 |
3,786 |
|
5 |
1720 |
2958400 |
553 |
305809 |
951160 |
513,3 |
90,6 |
263425,6 |
8201,6 |
474,88 |
78,12 |
6102,41 |
0,141 |
154,867 |
|
6 |
1500 |
2250000 |
453 |
205209 |
679500 |
293,3 |
-9,4 |
85995,6 |
89,1 |
469,55 |
-16,55 |
273,83 |
0,037 |
50,557 |
|
7 |
1320 |
1742400 |
478 |
228484 |
630960 |
113,3 |
15,6 |
12825,6 |
242,2 |
465,18 |
12,82 |
164,26 |
0,027 |
7,540 |
|
8 |
918 |
842724 |
448 |
200704 |
411264 |
-288,8 |
-14,4 |
83376,6 |
208,4 |
455,44 |
-7,44 |
55,30 |
0,017 |
49,017 |
|
9 |
794 |
630436 |
453 |
205209 |
359682 |
-412,8 |
-9,4 |
170362,6 |
89,1 |
452,43 |
0,57 |
0,33 |
0,001 |
100,156 |
|
10 |
1012 |
1024144 |
627 |
393129 |
634524 |
-194,8 |
164,6 |
37927,6 |
27080,8 |
457,72 |
169,28 |
28657,25 |
0,270 |
22,298 |
|
11 |
1058 |
1119364 |
364 |
132496 |
385112 |
-148,8 |
-98,4 |
22126,6 |
9689,9 |
458,83 |
-94,83 |
8992,88 |
0,261 |
13,008 |
|
12 |
1213 |
1471369 |
419 |
175561 |
508247 |
6,3 |
-43,4 |
39,1 |
1886,8 |
462,59 |
-43,59 |
1900,00 |
0,104 |
0,023 |
|
13 |
1225 |
1500625 |
392 |
153664 |
480200 |
18,3 |
-70,4 |
333,1 |
4961,4 |
462,88 |
-70,88 |
5023,97 |
0,181 |
0,196 |
|
14 |
1042 |
1085764 |
478 |
228484 |
498076 |
-164,8 |
15,6 |
27142,6 |
242,2 |
458,44 |
19,56 |
382,48 |
0,041 |
15,957 |
|
15 |
1071 |
1147041 |
521 |
271441 |
557991 |
-135,8 |
58,6 |
18428,1 |
3429,6 |
459,15 |
61,85 |
3825,91 |
0,119 |
10,834 |
|
16 |
1093 |
1194649 |
517 |
267289 |
565081 |
-113,8 |
54,6 |
12939,1 |
2977,1 |
459,68 |
57,32 |
3285,65 |
0,111 |
7,607 |
|
Σ |
19308 |
24134510 |
7399 |
3531243 |
8948979 |
0 |
0 |
834581 |
109668 |
7399 |
109177 |
2,331 |
490,65 |
|
|
среднее значение |
¯x = 1206,8 |
¯x2= 1508407 |
¯y = 462,4 |
¯y2= 220703 |
¯xy = 559311 |
¯A, %= 14,567 |
||||||||
|
σ |
228,39 |
82,79 |
||||||||||||
|
σ2 |
52161 |
6854,2 |
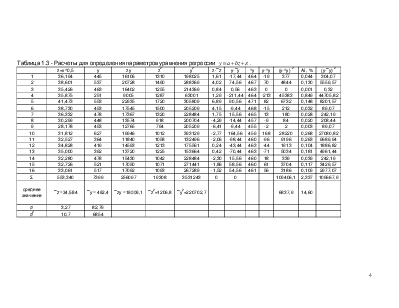
Таблица 1.3 -
Расчеты для определения параметров уравнения регрессии ![]() .
.
|
z=x^0,5 |
y |
zy |
z2 |
y2 |
z-¯z |
y-¯y |
^y |
y-^y |
(y-^y) 2 |
Ai , % |
(y-¯y) 2 |
|
|
1 |
36,194 |
445 |
16106 |
1310 |
198025 |
1,61 |
-17,44 |
464 |
-19 |
377 |
0,044 |
304,07 |
|
2 |
38,601 |
537 |
20728 |
1490 |
288369 |
4,02 |
74,56 |
467 |
70 |
4844 |
0,130 |
5559,57 |
|
3 |
35,426 |
463 |
16402 |
1255 |
214369 |
0,84 |
0,56 |
463 |
0 |
0 |
0,001 |
0,32 |
|
4 |
35,875 |
251 |
9005 |
1287 |
63001 |
1,29 |
-211,44 |
464 |
-213 |
45383 |
0,849 |
44705,82 |
|
5 |
41,473 |
553 |
22935 |
1720 |
305809 |
6,89 |
90,56 |
471 |
82 |
6732 |
0,148 |
8201,57 |
|
6 |
38,730 |
453 |
17545 |
1500 |
205209 |
4,15 |
-9,44 |
468 |
-15 |
212 |
0,032 |
89,07 |
|
7 |
36,332 |
478 |
17367 |
1320 |
228484 |
1,75 |
15,56 |
465 |
13 |
180 |
0,028 |
242,19 |
|
8 |
30,299 |
448 |
13574 |
918 |
200704 |
-4,29 |
-14,44 |
457 |
-9 |
84 |
0,020 |
208,44 |
|
9 |
28,178 |
453 |
12765 |
794 |
205209 |
-6,41 |
-9,44 |
455 |
-2 |
2 |
0,003 |
89,07 |
|
10 |
31,812 |
627 |
19946 |
1012 |
393129 |
-2,77 |
164,56 |
459 |
168 |
28220 |
0,268 |
27080,82 |
|
11 |
32,527 |
364 |
11840 |
1058 |
132496 |
-2,06 |
-98,44 |
460 |
-96 |
9196 |
0,263 |
9689,94 |
|
12 |
34,828 |
419 |
14593 |
1213 |
175561 |
0,24 |
-43,44 |
463 |
-44 |
1913 |
0,104 |
1886,82 |
|
13 |
35,000 |
392 |
13720 |
1225 |
153664 |
0,42 |
-70,44 |
463 |
-71 |
5034 |
0,181 |
4961,44 |
|
14 |
32,280 |
478 |
15430 |
1042 |
228484 |
-2,30 |
15,56 |
460 |
18 |
339 |
0,039 |
242,19 |
|
15 |
32,726 |
521 |
17050 |
1071 |
271441 |
-1,86 |
58,56 |
460 |
61 |
3704 |
0,117 |
3429,57 |
|
16 |
33,061 |
517 |
17092 |
1093 |
267289 |
-1,52 |
54,56 |
461 |
56 |
3186 |
0,109 |
2977,07 |
|
Σ |
553,340 |
7399 |
256097 |
19308 |
3531243 |
0 |
0 |
109406,1 |
2,337 |
109667,9 |
||
|
среднее значение |
¯z =34,584 |
¯y = 462,4 |
¯zy =16006,1 |
¯z2=1206,8 |
¯y2=220702,7 |
6837,9 |
14,60 |
|||||
|
σ |
3,27 |
82,79 |
||||||||||
|
σ2 |
10,7 |
6854 |
Выберем
в качестве модели уравнение регрессии ![]() .
Введем замену:
.
Введем замену: ![]() , получим линейное уравнение
парной регрессии
, получим линейное уравнение
парной регрессии ![]() . Все промежуточные расчеты
приведены в таблице 1.3.
. Все промежуточные расчеты
приведены в таблице 1.3.
Рассчитаем параметры уравнения, предварительно рассчитав
![]() ;
;
![]() ,
,
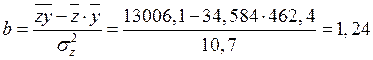 ;
;
![]() ,
,
![]() .
.
Рассчитаем линейный коэффициент парной корреляции:
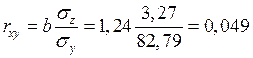 .
.
Близость ![]() к 0 означает отсутствие линейной связи
между признаками.
к 0 означает отсутствие линейной связи
между признаками.
Рассчитаем значение F-критерия Фишера:
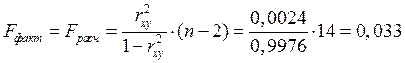 ,
,
![]() .
.
Так как ![]() , то необходимо принять гипотезу
, то необходимо принять гипотезу ![]() о случайной природе выявленной зависимости
и статистической незначимости параметров уравнения.
о случайной природе выявленной зависимости
и статистической незначимости параметров уравнения.
Воспользуемся формулой расчета индекса корреляции для нелинейной регрессии:
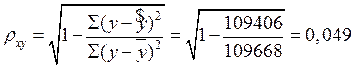 .
.
Рассчитаем средний коэффициент эластичности:
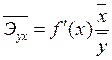 ;
;
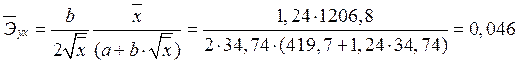 .
.
Оценивая коэффициент эластичности можно предположить, что с увеличением заработной платы и социальных выплат на 1%, потребительские расходы увеличатся на 0,046%.
Средняя
ошибка аппроксимации ![]() вышла за допустимые пределы
(8-10%), что говорит о неудачном выборе уравнения регрессии. Полученные оценки
параметров уравнения не позволяют использовать его для прогноза.
вышла за допустимые пределы
(8-10%), что говорит о неудачном выборе уравнения регрессии. Полученные оценки
параметров уравнения не позволяют использовать его для прогноза.
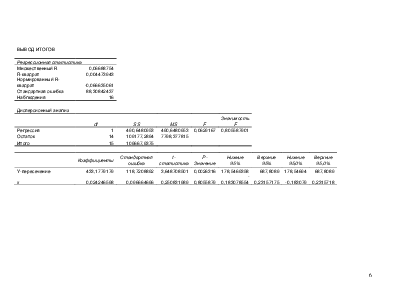
В таблице 1.4 представлены результаты регрессионного анализа для линейной функции, выполненные с помощью ППП Excel.
|
ВЫВОД ИТОГОВ |
||||||||
|
Регрессионная статистика |
||||||||
|
Множественный R |
0,06688754 |
|||||||
|
R-квадрат |
0,004473943 |
|||||||
|
Нормированный R-квадрат |
-0,066635061 |
|||||||
|
Стандартная ошибка |
88,30842437 |
|||||||
|
Наблюдения |
16 |
|||||||
|
Дисперсионный анализ |
||||||||
|
df |
SS |
MS |
F |
Значимость F |
||||
|
Регрессия |
1 |
490,6480953 |
490,6480953 |
0,0629167 |
0,805587901 |
|||
|
Остаток |
14 |
109177,2894 |
7798,377815 |
|||||
|
Итого |
15 |
109667,9375 |
||||||
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Y-пересечение |
433,1779179 |
118,7208892 |
3,648708501 |
0,0026316 |
178,5469358 |
687,8089 |
178,54694 |
687,8089 |
|
x |
0,024246598 |
0,096664696 |
0,250831989 |
0,8055879 |
-0,183078554 |
0,23157175 |
-0,183079 |
0,2315718 |
2. Контрольное задание 2
2.1 Имеются данные 12 месяцев по району города о рынке вторичного жилья, (у – стоимость квартиры, тыс. у.е.; х1 – размер жилой площади, м2; х2 – размер кухни, м2), задача 19. исходные данные представлены в таблице 2.1.
Таблица 2.1 – Исходные данные
|
у, тыс. у.е. |
22,5 |
25,5 |
19,2 |
13,6 |
25,4 |
17,8 |
18,0 |
21,1 |
16,5 |
23,0 |
16,2 |
17,2 |
|
х1, м2 |
37,2 |
58,0 |
60,2 |
52,0 |
44,6 |
31,2 |
26,4 |
20,7 |
22,4 |
35,4 |
28,4 |
22,7 |
|
х2, м2 |
7,6 |
9,4 |
9,5 |
8,1 |
7,4 |
6,3 |
5,9 |
5,5 |
5,7 |
6,8 |
6,5 |
6,0 |
Результаты расчетов приведены в таблице 2.2.
Таблица 2.2.
|
y |
x1 |
x2 |
yx1 |
yx2 |
x1x2 |
x12 |
x22 |
y2 |
^y |
Ai , % |
|
|
1 |
22,5 |
37,2 |
7,6 |
837 |
171 |
282,72 |
1383,8 |
57,76 |
506,25 |
20,74 |
0,078 |
|
2 |
25,5 |
58 |
9,4 |
1479 |
239,7 |
545,2 |
3364,0 |
88,36 |
650,25 |
22,04 |
0,136 |
|
3 |
19,2 |
60,2 |
9,5 |
1155,84 |
182,4 |
571,9 |
3624,0 |
90,25 |
368,64 |
21,99 |
0,145 |
|
4 |
13,6 |
52 |
8,1 |
707,2 |
110,16 |
421,2 |
2704,0 |
65,61 |
184,96 |
20,02 |
0,472 |
|
5 |
25,4 |
44,6 |
7,4 |
1132,84 |
187,96 |
330,04 |
1989,2 |
54,76 |
645,16 |
19,43 |
0,235 |
|
6 |
17,8 |
31,2 |
6,3 |
555,36 |
112,14 |
196,56 |
973,4 |
39,69 |
316,84 |
18,71 |
0,051 |
|
7 |
18 |
26,4 |
5,9 |
475,2 |
106,2 |
155,76 |
697,0 |
34,81 |
324 |
18,44 |
0,025 |
|
8 |
21,1 |
20,7 |
5,5 |
436,77 |
116,05 |
113,85 |
428,5 |
30,25 |
445,21 |
18,28 |
0,133 |
|
9 |
16,5 |
22,4 |
5,7 |
369,6 |
94,05 |
127,68 |
501,8 |
32,49 |
272,25 |
18,50 |
0,121 |
|
10 |
23 |
35,4 |
6,8 |
814,2 |
156,4 |
240,72 |
1253,2 |
46,24 |
529 |
19,26 |
0,162 |
|
11 |
16,2 |
28,4 |
6,5 |
460,08 |
105,3 |
184,6 |
806,6 |
42,25 |
262,44 |
19,47 |
0,202 |
|
12 |
17,2 |
22,7 |
6 |
390,44 |
103,2 |
136,2 |
515,3 |
36 |
295,84 |
19,10 |
0,111 |
|
∑ |
236 |
439,2 |
84,7 |
8813,5 |
1684,6 |
3306,4 |
18240,7 |
618,47 |
4800,8 |
236,0 |
1,872 |
|
средние значения |
19,67 |
36,60 |
7,058 |
734,46 |
140,38 |
275,5 |
1520,1 |
51,54 |
400,1 |
19,67 |
15,60 |
|
σ |
3,65 |
13,43 |
1,31 |
||||||||
|
σ2 |
13,29 |
180,50 |
1,72 |
2.1.
Рассматриваем уравнение вида: ![]() .
.
При переходе
к стандартизированному виду получим: ![]() ,
,
где:
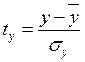 ,
, 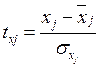 - стандартизированные переменные;
- стандартизированные переменные; ![]() - стандартизированные
коэффициенты,
- стандартизированные
коэффициенты,
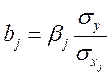 ,
, ![]() .
.
Коэффициенты
![]() , в частности, для
, в частности, для ![]() ,
определяются из системы уравнений:
,
определяются из системы уравнений:
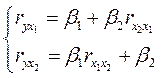 ,
,
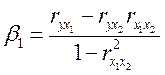 ,
, 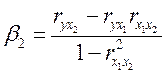 ;
;
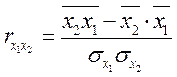 ,
, 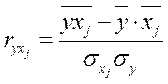 .
.
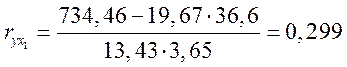 ,
, ![]() ;
;
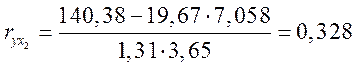 ,
, ![]() ;
;
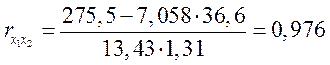 ,
,
![]() ;
;
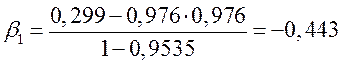 ,
, 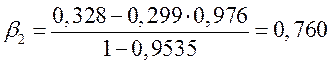 .
.
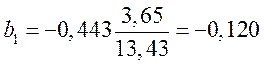 ,
, 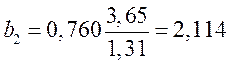 ;
;
![]() .
.
Стандартизированная форма уравнения примет вид:
![]() .
.
Естественная форма уравнения регрессии имеет вид:
![]() .
.
2.2 Для выяснения относительной силы влияния факторов на результативный признак рассчитываются средние коэффициенты эластичности:
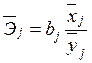 ,
,
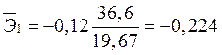 ,
, 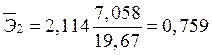 .
.
Полученные результаты позволяют сделать следующие выводы:
2.3 Для
оценки статистической значимости коэффициентов ![]() и
и ![]() , рассчитаем значения t-критерия Стьюдента как квадратные
корни из соответствующих частных F-критериев
Фишера:
, рассчитаем значения t-критерия Стьюдента как квадратные
корни из соответствующих частных F-критериев
Фишера:
![]() ,
,
![]() ,
,
где, 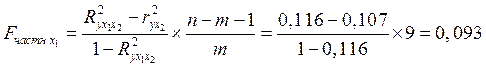 ,
,
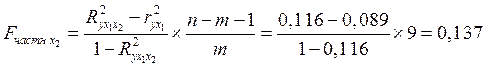 ,
,
где,
![]() -
коэффициент детерминации парной корреляции.
-
коэффициент детерминации парной корреляции.
Сравнивая
полученные значения t-критерия с табличным значением ![]() , приходим к следующим выводам:
, приходим к следующим выводам:
![]() коэффициент
регрессии
коэффициент
регрессии ![]() является величиной, статистически
незначимой, ненадежной в силу того, что она формируется под действием случайных
факторов;
является величиной, статистически
незначимой, ненадежной в силу того, что она формируется под действием случайных
факторов;
![]() коэффициент
регрессии
коэффициент
регрессии ![]() , так же, является величиной, статистически
незначимой, ненадежной в силу того, что она формируется под действием случайных
факторов;
, так же, является величиной, статистически
незначимой, ненадежной в силу того, что она формируется под действием случайных
факторов;
Для оценки значимости уравнения в целом рассчитаем значение F-критерия Фишера:
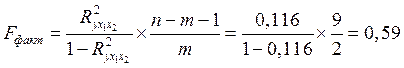
![]() ,
, ![]() , следовательно гипотеза H0 не отклоняется уравнение статистически незначимо в
целом.
, следовательно гипотеза H0 не отклоняется уравнение статистически незначимо в
целом.
2.4
В таблице 2.2
приведен расчет средней ошибки аппроксимации. ![]() вышла
за допустимые пределы (8-10%), что говорит о плохом качестве модели.
вышла
за допустимые пределы (8-10%), что говорит о плохом качестве модели.
2.5 Составим матрицы парных и частных коэффициентов корреляции:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.