


Задача 2. Применение графического метода при построении оптимального плана работы 2-х погрузчиков на 2-х площадках
Двум
погрузчикам разной мощности за 24 часа требуется погрузить на 1-й площадке ![]() , т, на 2-й -
, т, на 2-й - ![]() , т. 1-й погрузчик на 1-й площадке может погрузить
, т. 1-й погрузчик на 1-й площадке может погрузить ![]() , т/ч, на 2-й -
, т/ч, на 2-й - ![]() , т/ч. 2-й погрузчик на 1-й площадке -
, т/ч. 2-й погрузчик на 1-й площадке - ![]() , т/ч, на 2-й -
, т/ч, на 2-й - ![]() , т/ч. Стоимость работ, связанных с погрузкой 1 т 1-м погрузчиком на 1-й
площадке,
, т/ч. Стоимость работ, связанных с погрузкой 1 т 1-м погрузчиком на 1-й
площадке, ![]() , ден.ед., на 2-й площадке -
, ден.ед., на 2-й площадке - ![]() , ден.ед. 2-м погрузчиком на 1-й площадке -
, ден.ед. 2-м погрузчиком на 1-й площадке - ![]() , ден.ед., на 2-й площадке -
, ден.ед., на 2-й площадке - ![]() , ден.ед. Требуется составить оптимальный план, т.е. определить какой
объем работ должен выполнить каждый погрузчик на каждой площадке (т), чтобы
стоимость всех работ по погрузке была минимальной.
, ден.ед. Требуется составить оптимальный план, т.е. определить какой
объем работ должен выполнить каждый погрузчик на каждой площадке (т), чтобы
стоимость всех работ по погрузке была минимальной.
|
1 площадка |
2 площадка |
Время, ч |
|
|
1 погрузчик |
|
|
24 |
|
2 погрузчик |
|
|
24 |
|
задание |
|
|
|
1 площадка |
2 площадка |
Время, ч |
|
|
1 погрузчик |
|
|
24 |
|
2 погрузчик |
|
|
24 |
|
задание |
|
|
Решение:
1. Построим математическую модель:
Обозначим через ![]() , i,j=
, i,j=![]() объем работ (т) i-го
погрузчика на j-й площадке. Тогда целевая функция,
выражающая затраты, связанные с выполнением работ, имеет вид:
объем работ (т) i-го
погрузчика на j-й площадке. Тогда целевая функция,
выражающая затраты, связанные с выполнением работ, имеет вид:
Z=8![]() + 8
+ 8![]() + 11
+ 11![]() + 13
+ 13![]() min
min
При ограничениях:
- на время работы: ![]() ;
;
![]() (2)
(2)
- на выполнение работы: ![]() +
+![]()
- условие не отрицательности: ![]() , I,j=
, I,j=![]()
2. Решим задачу графическим методом. Для этого сведем задачу с 4-мя переменными в задачу с 2-мя переменными:
![]()
![]()
![]()
![]()
![]() min
min
![]() (1)
(1)
(232-![]() )+(170-
)+(170-![]() )
)![]() 2413
2413
![]() (2)
(2)
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]()
![]()
Функция Z=8![]() + 8
+ 8![]() + 11
+ 11![]() + 13
+ 13![]() достигает своего минимума в тех же точках, что и функция :
достигает своего минимума в тех же точках, что и функция :
![]() =
=![]()
Построим область допустимых решений:
Областью допустимых решений является многоугольник ABCDEF
Проведем вектор
градиентного направления ![]() =(4; 6). Для удобства построим 25
=(4; 6). Для удобства построим 25![]() =(100; 150).
=(100; 150).
Перпендикулярно
![]() строим
линию уровня целевой функции Z=0.
Перемещаем Z=0 в направлении
строим
линию уровня целевой функции Z=0.
Перемещаем Z=0 в направлении ![]() до крайней точки касания с областью допустимых решений – точки D.
до крайней точки касания с областью допустимых решений – точки D.
В т. D находится оптимальный план. Для определения координат т. D решим систему уравнений:
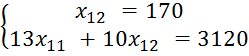
![]()
![]() 109
109
Тогда ![]() ;
; ![]() ;
;
Z=3120
Вывод: первый погрузчик должен погрузить 123т. на первой площадке, 170 – на второй площадке; второй погрузчик должен погрузить 109т. на первой площадке. При этом стоимость работ будет минимальной и составит 3120 денежных единиц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.