Построение дискретного ряда распределения по группировочному признаку. Анализ показателей бухгалтерского баланса путём расчёта статистических показателей структуры и динамики

число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.

14 предприятий имеет размер основных средств больше среднего арифметического, а 16 – меньше.

Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Так как эксцесс равен 0,037, то можно сделать вывод о том, что распределение относительно остроконечное.

Первая группа предприятий:

№ предприятия	Прибыль от продаж т.р.	Основные средства т.р.
8	7659	29351
17	38983	11553
19	6310	13488
21	8657	19107
22	17815	18184
24	9250	20705
26	4908	14546
27	3016	22661
28	20950	23480
29	27133	25590
30	11500	18650
Сумма	156181	217315

Вторая группа предприятий:

№ предприятия	Прибыль от продаж т.р.	Основные средства т.р.
4	13115	46234
6	2381	47067
10	1089	40633
15	2014	33465
16	7469	32176
18	2586	40150
20	8336	39282
Сумма	36990	279007

Третья группа предприятий:

№ предприятия	Прибыль от продаж т.р.	Основные средства т.р.
3	4678	52187
5	4809	56932
7	65920	54356
9	4817	62651
11	20995	64567
12	5515	58711
14	3412	57195
23	1526	62741
Сумма	111672	469340

Четвертая группа предприятий:

№ предприятия	Прибыль от продаж т.р.	Основные средства т.р.
13	10786	87210
25	6564	72342
Сумма	17350	159552

Пятая группа предприятий:

№ предприятия	Прибыль от продаж т.р.	Основные средства т.р.
1	24774	106447
2	9210	92805
Сумма	33984	199252

Вывод: 18 предприятий из 30 (60%) имеют основные средства, стоимость которых не превышает 49553 т.р., 4 предприятия (13%) имеют основные средства, стоимость которых превышает 68553 т.р. Прибыль всех 30 предприятий равна 356177 т.р., сумма основных средств всех предприятий равна – 1324466 т.р..

Задание 2

Для выявления зависимости между экономическими показателями провести аналитическую группировке показателей предприятий, с равными интервалами, выделив 4 или 5 групп. Рассчитать коэффициенты вариации. Объяснить расхождения в значениях полученных коэффициентов.

Решение:

Используя данные, полученные при решении задания 1, получим:

Рассчитаем среднее квадратическое отклонение, зная, что средняя арифметическая ряда равна – 44148,87:

Средняя величина хi	Частоты fi		2	2fi
21053	11	23095,87	533419211,1	5867611322
40053	7	4095,87	16776151,06	117433057,4
59053	8	14904,13	222133091,1	1777064728
78053	2	33904,13	1149490031	2298980062
97053	2	52904,13	2798846971	5597693942
	30		4720665455	15658783112

Среднее квадратическое отклонение для вариационного ряда определяется по формуле:

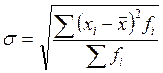
Подставив данные получим

s = 22846,4316

Коэффициент вариации равен:

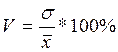=22846,4316/44148,86667*100%=51,7%, так как коэффициент вариации больше 33 %, то можно сделать вывод, что совокупность неоднородна и среднее для неё не истинно.

Задание 3

Выполнить анализ показателей бухгалтерского баланса путём расчёта статистических показателей структуры и динамики.

Решение:

Прирост равен разности между суммой на конец и начало периода.

Темп роста – частное между показателем на конец и на начало периода, выраженное в процентах.

Темп прироста равен 100% минус темп роста.

Проведённые расчёты подставим в виде таблицы (таблица 1), предварительно проведя группировку и уплотнение статей баланса.

Расчётная таблица 1.

	На начало периода	На конец периода	Удельный вес показателя в валюте баланса(%)	Удельный вес показателя в разделе баланса (%)	Прирост	Темп роста	Темп прироста
АКТИВ
1	2	3	4	5	6	7	8
I. Нефинансовые активы Основные средства (первоначальная стоимость) *	4 087 680,00	4 369 558,10	-	-	281 878,10	106,9	-6,9
Амортизация основных средств *	2 621 696,02	2 820 541,01	-	-	198 844,99	107,6	-7,6
Основные средства (остаточная стоимость)	1 465 983,98	1 549 017,09		98,0	83 033,11	105,7	-5,7
Материальные запасы	29 602,21	38 813,32		2,0	9 211,11	131,1	-31,1
Итого по разделу I	1 495 586,19	1 587 830,41	94,7	100,0	92 244,22	106,2	-6,2
II. Финансовые активы Денежные средства учреждения	14 416,48	17 017,59		17,4	2 601,11	118,0	-18,0
Расчеты по выданным авансам	39 719,14	185 500,81		47,9	145 781,67	467,0	-367,0
Расчеты с подотчетными лицами	28 749,24	9 357,92		34,7	-19 391,32	32,6	67,4
Итого по разделу II	82 884,86	211 876,32	5,3	100,0	128 991,46	255,6	-155,6
БАЛАНС	1 578 471,05	1 799 706,73	100,0		221 235,68	114,0	-14,0
ПАССИВ
Расчеты по платежам в бюджеты	7 108,00	2 784,07	0,2		-4 323,93	39,2	60,8
IV. Финансовый результат                                                                                      Финансовый результат учреждения	1 571 363,05	1 796 922,66	99,8	100,0	225 559,61	114,4	-14,4
Финансовый результат прошлых отчетных периодов	1 571 363,05	1 796 922,66		100,0	225 559,61	114,4	-14,4
Доходы будущих периодов	0,00	0,00		0,0	0,00	0,0	0,0
БАЛАНС	1 578 471,05	1 799 706,73	100,0		221 235,68	114,0	-14,0

<*> Данные по этим строкам в валюту баланса не входят.

Задание 4

Произвести 25% механическую выборку из совокупности, по показателю – прибыль от продаж. С вероятностью 0,954 рассчитать границы изменения средней величины в генеральной совокупности и сравнить с результатом, полученным на основе расчёта по выборочной совокупности. Начало отбора начать с номера предприятия, совпадающего с номером варианта. Сформулировать вывод.

Решение:

Механическая выборка предполагает, что отбор производится через равные промежутки. Генеральная совокупность состоит из 39 предприятий, проведём выборку предприятий (25%), начав с предприятия №4, шаг отсчёта равен 4 (1/0,25=4):

Рассчитаем величину средней ошибки механического бесповторного отбора по упрощённой форме, для этого сначала определим дисперсию признака в выборочной совокупности, при том, что среднее по выборочной совокупности равно 14613,67:

№ предприятия	Прибыль от продаж т.р.
4	24774	10160,33	103232305,7
8	4809	-9804,67	96131553,81
12	4817	-9796,67	95974743,09
16	10786	-3827,67	14651057,63
№ предприятия	Прибыль от продаж т.р.
20	38983	24369,33	593864244,6
24	8657	-5956,67	35481917,49
28	6564	-8049,67	64797187,11
32	27133	12519,33	156733623,6
36	5000	-9613,67	92422650,87
	131523		1253289284

Подставив данные получим выборочную дисперсию:

s² = 139254364,9

Определим величину средней ошибки механического бесповторного отбора по упрощённой формуле:

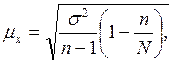 где N – объём генеральной совокупности, n – объём выборки.

Подставив данные получим:

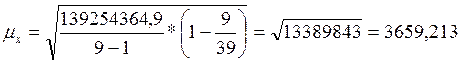
Рассчитаем границы измерения средней характеристики генеральной совокупности по материалам выборки, воспользуемся следующими формулами:

,

, где - средняя выборочной совокупности, - средняя генеральной совокупности.

= 14613,67

 (t – коэффициент доверия, показатель, определяющий размер ошибки в зависимости от того, с какой вероятностью (в нашем задании 0,954) она находится. Значения даны в специальных таблицах[1]).

14613,67-7318,43< >14613,67+7318,43

7295,24< < 21932,09

Таким образом, с вероятностью 0,954 мы утверждаем, что прибыль от продаж на одном предприятии в генеральной совокупности будет