Статистическая сводка и группировка данных. Выборочный метод в статистических исследованиях. Статистическое изучение взаимосвязей

Вариант №7

Раздел 1. Статистическая сводка. Группировка данных.

Задание 1.

Результативным признаком для данного варианта является «Чистая прибыль отчетного периода», группировочным – «Запасы». Исходные данные представлены в таблице 1.1

                    Таблица 1.1                                                                   Таблица 1.2

№ п/п	Чистая прибыль отчетного периода, т.р.	Запасы, т.р.
3	1007
4	22364
5	7850
6	5076
7	11429
8	5862	27850
9	1523	26781
10	24971	21342
11	8124	84013
12	1478	10328
13	941	23805
14	18180	11774
15	3030	11559
16	13123	32952
17	2271	20645
18	2017	54864
19	6154	23256
20	1170	76561
21	2189	13942
22	1776	74681
23	1621	33516
24	9882	15197
25	1235	28310
26	8882	40355
27	4813	39373
28	1653	15002
29	4589	47844
30	1579	27833
31	1570	17210
32	1321	19700
33	1754	20600
34	3501	17840
35	2160	11457
36	2363	13400
37	1007	8100
38	1145
40	998

8100
10328
11457
11559
11774
13400
13942
15002
15197
17210
17840
19700
20600
20645
21342
23256
23805
26781
27833
27850
28310
32952
33516
39373
40355
47844
54864
74681
76561
84013

Задание 1. Для построения ряда распределения по группировочному признаку, расположим значения признака в порядке возрастания (см. Табл. 1.2).

Величина интервала группировки определится по формуле: ,

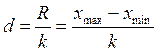где:  - величина интервала;  - число групп;  - размах вариации;  - максимальное значение группировочного признака в совокупности;  - минимальное значение групировочного признака.

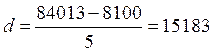
Подсчитав количество предприятий в каждой группе, получим ряд распределения предприятий по величине запаса. Рассчитаем показатели центра распределения: , , .

Среднюю величину в интервальном ряду распределения определим по формуле средней арифметической взвешенной:

,

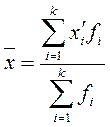где:  - средняя величина;  - среднее значение признака в интервале (цент интервала);  - число единиц совокупности в интервале (частота).  Определение показателе уравнения приводится в таблице 1.3.

Таблица 1.3

Предприятия по объемам запаса, тыс. р.				Накопленная частота
8100-23283	16	15691	251061	16
23283-38465	7	30874	216117	23
38465-53648	3	46057	138170	26
53648-68830	1	61239	61239	27
68830-84013	3	76422	229265	30
Итого	30	-	895852	-

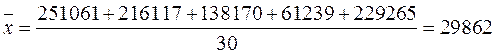 тыс. р.

Для определения величин моды и медианы используются следующие формулы: ,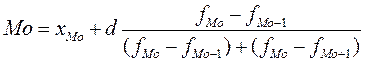

где:  - начало модального интервала;  - частота, соответствующая модальному интервалу;  - предмодальная частота;  - послемодальная частота.

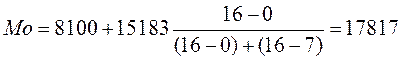 тыс. р.

,

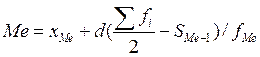где:  - нижняя граница медианного интервала;  - накопленная частота интервала, предшествующая медианному;  - частота медианного интервала. Медианным является интервал 8100-23283 тыс. р., так как в этом интервале накопленная частота больше половины всей суммы.

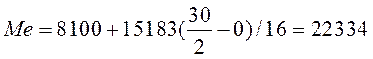 тыс. р.

Вычислим показатель ассиметрии:

,

 

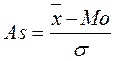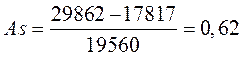
Так как  (17817<22334<29862) наблюдаем правостороннюю ассиметрию. Для оценки существенности показателя ассиметрии определим ее среднюю квадратическую ошибку, которая зависит от количества наблюдений :

,

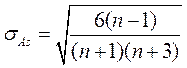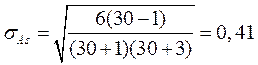
Так как 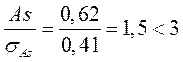, то ассиметрия несущественна, ее наличие объясняется влиянием различных случайных обстоятельств.

Для симметричного ряда можно рассчитать дополнительно показатель эксцесса:

,

где:  - доля (%) количества вариантов, лежащих в интервале, равном половине среднеквадратического отклонения в ту и другую сторону от средней арифметической. Имеем , , . Кривая распределения является в данном случае  островершинной.

Задание 2. Для выявления зависимости между экономическими показателями деятельности предприятий (см. таблицу 1.1, 1.2) проведем аналитическую группировку их показателей. Выделим пять групп с равными интервалами. Относительным показателем уровня вариации признака является коэффициент вариации (). Он представляет собой отношение среднего квадратического отклонения к средней величине признака и выражается обычно в процентах: ,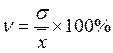

где:  - среднее квадратическое отклонение;  - средняя величина. Расчет средней величины проведем по средней арифметической простой (при расчете по исходным данным) и по средней арифметической взвешенной (при расчете по аналитической таблице). Группировка предприятий по объемам запаса представлена в таблице 1.4.

Таблица 1.4

Группы предприятий по величине запасов, млн. р.	Число предприятий в группе	Предприятие	Всего по группе, тыс. р.	Средний размер запаса по группе, тыс. р.
8100-23283	16	10, 12, 14, 15, 17, 19, 21, 24, 28, 31-37	251352	15710
23283-38465	7	8, 9, 13, 16, 23, 25, 30	201047	30150
38465-53648	3	26, 27, 29	127572	42524
53648-68830	1	18	54864	54864
68830-84013	3	11, 20, 22	235255	78418
Итого	30	х	870090

и расчете по исходным данным  по средней арифметической и  выражается обычно в процентах

Формулы для расчетов средних величин в зависимости от исходных данных:

,  .

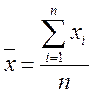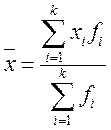где:  - численность совокупности;  - варианта или значение признака (для интервального ряда имеет среднее значение ),  - частота повторения индивидуального значения признака (его вес).

Для расчета среднего квадратического отклонения используем следующие формулы:

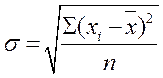 при расчете по исходным данным.

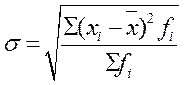 - при расчете по сгруппированным данным.

Расчет показателей вариации для предприятий произведем в таблице