Приложение 2
Протокол формирующей части эксперимента в группе 2.
Цель: сформировать у испытуемых способ сокращенного умножения содержательно-теоретическим типом обобщения.
Предметный материал -
картонные фигурки: квадрат со стороной ![]() ,
квадрат со стороной
,
квадрат со стороной ![]() , квадрат со стороной
, квадрат со стороной ![]() и два прямоугольника
и два прямоугольника ![]() (см. рис.).
(см. рис.).
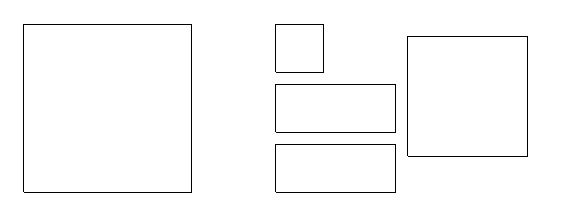
|
№ |
Время |
Этап (название) |
Что делает ведущий |
Что делают испытуемые |
|
1 |
20 |
Формула как модель равенства объектов |
Задает условия выполнения предметного действия. Сообщает, что полученная учащимися модель является формулой сокращенного умножения |
Выполняют предметное действие, результат моделируют на математическом языке |
|
2 |
10 |
Доказательство формулы |
Отмечает необходимость доказательства формулы |
Доказывают формулу с помощью распределительного закона и знания о степени |
|
3 |
10 |
Проверка уяснения |
Контролирует правильность выполнения заданий |
Выполняют задания на применение формулы |
«Ведущий (В): тема
сегодняшнего урока «Формула сокращенного умножения». Урок начнем с выполнения
задания. На столе каждого из вас лежит набор из геометрических фигур. Вам нужно
сравнить квадрат со стороной ![]() и набор других
фигур, и результат сравнения записать на математическом языке. Каждый пытается
сделать это самостоятельно.
и набор других
фигур, и результат сравнения записать на математическом языке. Каждый пытается
сделать это самостоятельно.
Ученики самостоятельно выполняют предметное действие.
Т: У меня получилось, что все фигурки укладываются в большой квадрат.
Р: И у меня получилось также.
В: Т., выходи к доске и попробуй начертить то, что у тебя получилось.
Т. выходит к доске и изображает на доске результат сравнения:

В: действительно, так. У кого не получился такой результат, попробуйте еще раз поместить все фигурки в большой квадрат, таким образом, как показано на доске.
Ученики выполняют указанное действие.
В: полученные результаты сравнения нам нужно зафиксировать в виде модели на математическом языке. Как нам это сделать? Как мы можем алгебраически записать полученное равенство фигур?
Ученики затрудняются ответить.
В: Давайте каждую фигуру попробуем записать на алгебраическом языке. Подумайте, почему все фигурки уместились в большой квадрат?
Л: потому что квадрат по площади такой же, как все фигурки вместе взятые.
В: верно. То есть, мы получили равенство площадей фигур. А можем мы теперь записать алгебраически такую характеристику фигуры как площадь? Мы знаем, как её находить?
Р: Да. Например, площадь квадрата равна стороне квадрата умноженной на саму себя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.