Рабочая программа по дисциплине "Теория автоматического управления". Варианты заданий к контрольной работе и пример выполнения задания, страница 5

Для построения АФЧХ на комплексной плоскости необходимо в уравнении передаточной функции выделить действительную и мнимую части, для этого числитель и знаменатель последнего выражения умножаем на сопряженное число знаменателю, т.е. на ((75×w² – 3000) – j×(8×w^{3 –} 550×w)). При расчетах помним, что j = ;  j² = -1;  j³ = -j.

W(jw) = =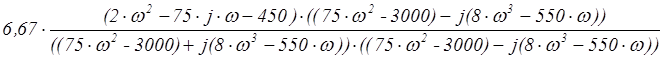

==

= .

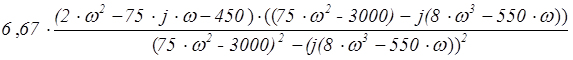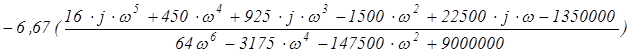Вместо j в формулу подставляем  j = ; j² = -1, получим:

W(jw)=.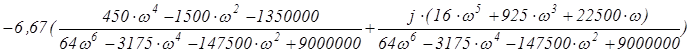

Модуль:

A(w) =;

Аргумент:

j(w) =,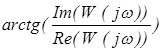

где Re(W(jw)) – действительная часть частотной передаточной функции; Im(W(jw)) – мнимая часть частотной передаточной функции.

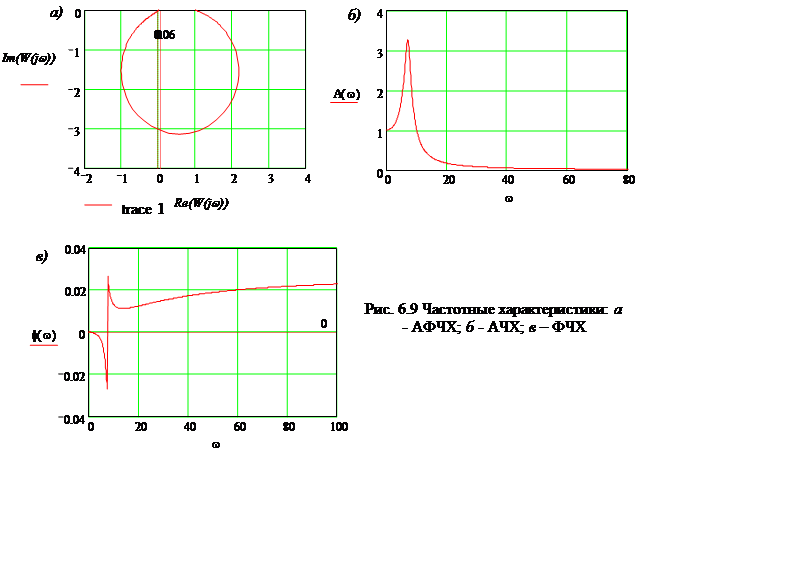
Подставим числовые значения частоты w = 0, 0.1,..1000, выполним расчеты и построим частотные характеристики АФЧХ, АЧХ, ФЧХ (рис. 6.9). Расчеты и построение графиков выполнено в программе MATHCAD.

Задание 4

Используя данные задания 1, провести анализ устойчивости системы, с помощью одного из алгебраических критериев устойчивости и одного из частотных. Если система неустойчива, то определить пути достижения устойчивости.

Анализ устойчивости по алгебраическому критерию Гурвица

Характеристическое уравнение разомкнутой системы по задающему воздействию X(p) (знаменатель передаточной функции,  смотри задание 2):

D(p) = 0,048p³ + 0,45p² + 3,3p + 18 = 0,

где a₀ = 0,048;      a₁ = 0,45;    a₂ = 3,3;      a₃ = 18.

Составим матрицу:

= 

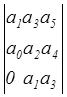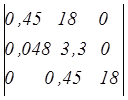
Условия устойчивости:

a₀ > 0;   a₁ > 0;       a₂ > 0;        a₃ > 0;          D₂ = a₁a₂ – a₀a₃ > 0.

Проверим выполнение этих условий.

a₀ = 0,048 > 0;        a₁ = 0,45 > 0;      a₂ = 3,3 > 0;         a₃ = 18 > 0.

Выразим определители Гурвица:

.

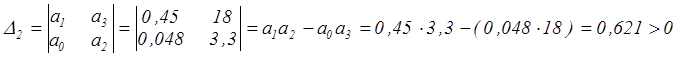Вывод: Условие D₂ > 0 выполняется, следовательно, система устойчива в разомкнутом состоянии по задающему воздействию.

Анализ устойчивости по критерию Михайлова

Анализ устойчивости системы этим методом сводится к построению по характеристическому многочлену замкнутой системы (знаменатель передаточной функции) комплексной частотной функции. Запишем знаменатель передаточной функции замкнутой системы по задающему воздействию (см. задание 2).

D(p) = (А₁p² + А₂p + А₃)×(A₄p + A₅) + (B₁p + B₂)×B₅p + (B₁p + B₂) × (B₂p + B₄) =

= (0,06p² + 0,1p +3)×(0,8p + 6) + (0,1p +3)×0,1p + (0,1p + 3)×(0,8p + 6).

Обозначим: p = jw, запишем:

D(jw) =(0,06× (j×w)² + 0,1× (j×w) +3)×(0,8× (j×w) + 6) + (0,1× (j×w) +3)×0,1× (j×w) +

+ (0,1× (j×w) + 3)×(0,8× (j×w) + 6).

Так как j = ; j² = -1; j³ = -j, то с учетом этого получим:

D(jw) = -0,048×j×w³ – 0,53×w² + 6,3× j×w +36;

Выделим действительную и мнимую часть комплекснозначной функции:

D(w) = (- 0,53×w²+36 )+ j× (6,3×w  – 0,048×w³);

D(w) = u(w) + j× v(w);

u(w) = Re(D(w));   v(w) = Im (D(w))

Подставим числовые значения частоты w = 0, 0.1..1000, выполним расчеты и построим АФЧХ (рисунок  3.10). Расчеты и построение графиков выполнены в программе MATHCAD.

Вывод: система автоматического управления в замкнутом состоянии устойчива, так как годограф Михайлова при изменении частоты w от нуля до бесконечности, начинаясь при w = 0 на вещественной положительной полуоси, обходит последовательно только против часовой стрелки три квадранта координатной плоскости (так как порядок характеристического уравнения третий), и уходит в бесконечность в третьем квадранте координатной плоскости.

Задание 5

Используя данные задания 1 и приняв f(t) = 0, определить значения установившейся ошибки системы.

Найдём значение установившейся ошибки, принимая p = 0:

К_замк. = W_замк.XY(0) = 18/36 = ½;

K_раз = W_разXY (0) = 18/18 = 1.

Ошибка:

E = ;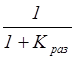

E = ½.

ВОПРОСЫ к ЭКЗАМЕНу

1.  Содержание понятий: «система», «регулирование», «управление», «объект управления», «управляемая величина», «возмущающее воздействие», «координата». Два рода операций в производственном процессе: рабочие операции, операции управления.

2.  Основные принципы управления.

3.  Блок-схема системы автоматического управления.