Номер варианта контрольной работы выбирается по двум последним цифрам номера зачетной книжки (таблица 3.1). Коэффициенты уравнений выбираются по таблице 3.2. Например: номер Вашей зачетной книжки 99-777. Ваш вариант 77 система уравнений в таблице 3.1 под номером 8. Значения коэффициентов в таблице 3.2 под номером 7.
Дана система уравнений, описывающих поведение некой системы автоматического управления:
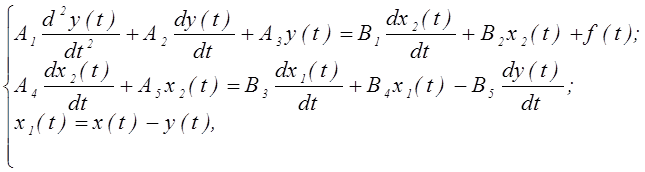
где: x(t) – входное воздействие (координата); y(t) – выходное воздействие (координата); x1(t), x2(t) – промежуточные координаты системы; f(t) – возмущающее воздействие; A1, A2, A3, A4, A5, B1, B2, B3, B4, B5 – постоянные коэффициенты.
A1 = 0,06; A2 = 0,1; A3 = 3; A4 = 0,8; A5 = 6;
B1= 0,1; B2= 3; B3= 0,8; B4= 6; B5= 0,1.
Используя преобразования Лапласа, представить уравнения в операторной форме, определить передаточные функции и построить структурную схему.
1) Строим структурную схему для первого уравнения системы:
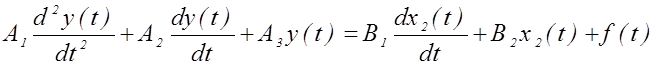 ;
;
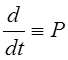 ;
;
 |
Y(p) = 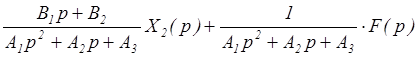 ;
;
W1 (p) = 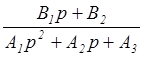 ;
;
W2 (p) =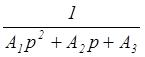 .
.
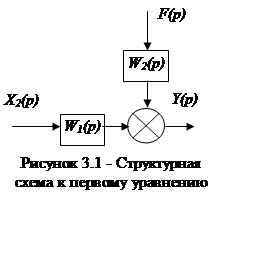
Y(p) = W1 (p) X2(p) + W2 (p) F(p)
Строим структурную схему (рисунок 3.1)
2) Строим структурную схему для второго уравнения:
A4 p X2(p) +A5 X2(p) = B3 p X1(p) +B4 X1(t) – B5 p Y(p);
(A4 p + A5) X2(p) = (B3 p + B4) X1(p) – B5 p Y(p);
X2(p) =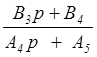 X1(p)
–
X1(p)
– 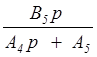 Y(p);
Y(p);
W3 (p) = 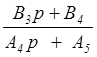 ; W4(p)
=
; W4(p)
= 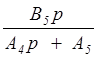 ;
;
X2(p) = W3 (p) X1(p) – W4(p) Y(p).
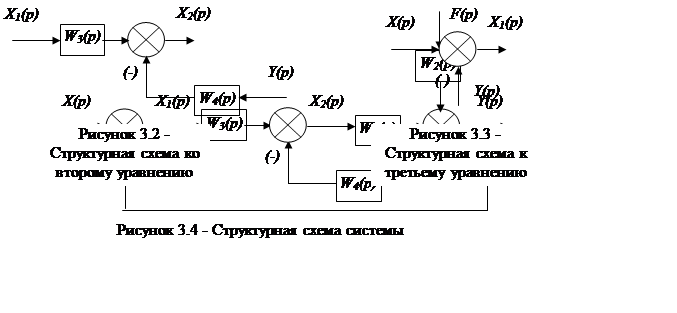
Строим структурную схему (рисунок 3.2)
3) Строим структурную схему для третьего уравнения:
X1(p) = X(p) – Y(p)
Строим структурную схему (рисунок 3.3).
 |
Используя правила эквивалентных преобразований, упростить схему, полученную в задании 1, до одного звена с обратной связью; определить передаточные функции по задающему и возмущающему воздействиям замкнутой и разомкнутой системы по цепи обратной связи, а также коэффициент усиления.
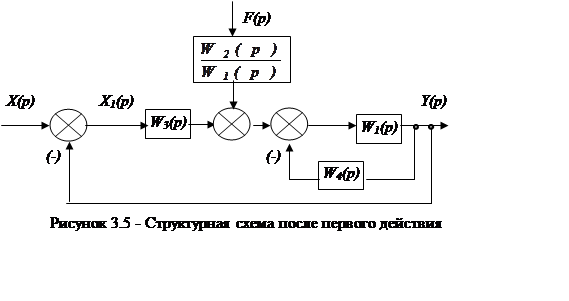 |
Второй шаг преобразований. Упростим обратную связь (рисунок 3.6):
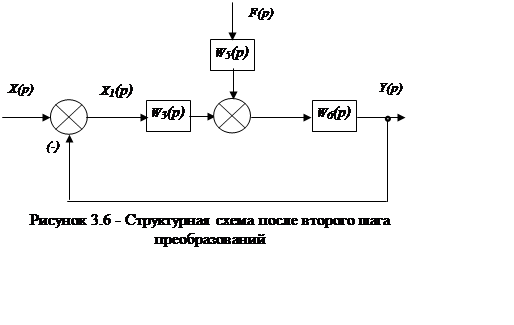 |
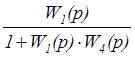 .
.
Третий шаг преобразований. Переносим сумматор через звено W3(p) влево:
W7(p) = W2(p)/(W1(p)×W3(p)),
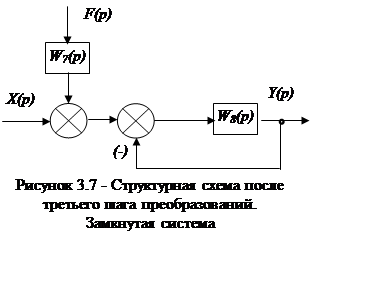
последовательно соединенные звенья W3(p) и W6(p)объединяем в одно звено с передаточной функцией W8(p) (рисунок 3.7):
W8(p) = 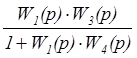 .
.
Запишем уравнение для определения выходной координаты Y(p):
Y(p) = [X(p)
+ F(p) ×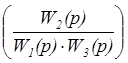 ] ´
] ´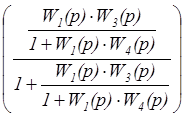 =
=
= [X(p) + F(p) ×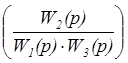 ] ´
] ´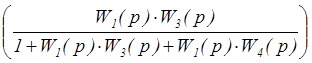 =
=
= 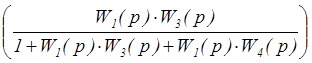 × X(p)
+
× X(p)
+ 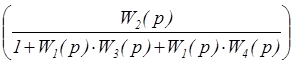 × F(p).
× F(p).
 |
Используя принцип суперпозиции, найдем передаточную функцию замкнутой системы сначала по задающему воздействию, а затем по возмущающему воздействию:
F(p) = 0; WXY(p) =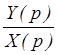 =
= 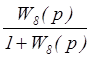 =
=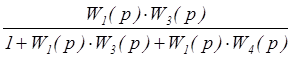 ;
;
X(p) = 0; WFY = 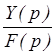 =
= 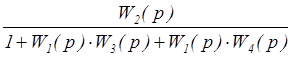 ;
;
W1(p) =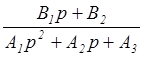 =
=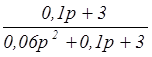 ;
;
W2(p) = 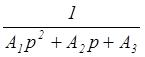 =
=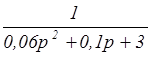 ;
;
W3(p) = 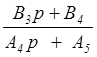 =
=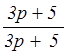 =1; W4(p) =
=1; W4(p) = 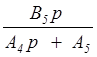 =
=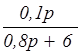 .
.
Тогда
WXY(p) =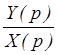 =
=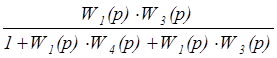 =
=
= 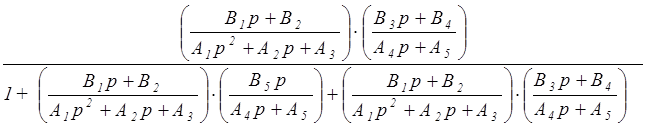 =
=
=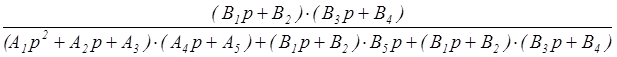 =
=
= 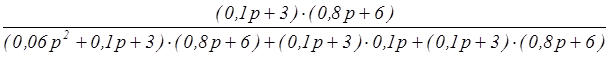 = =
= =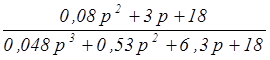 ;
;
WFY(p) = 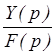 =
= 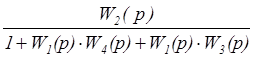 =
=
= 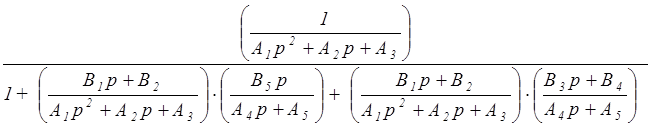 =
=
= 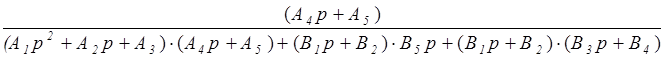 =
=
= 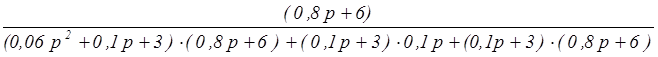 =
=
=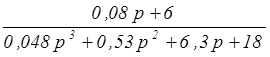 ;
;
Передаточная функция разомкнутой системы (рисунок 3.8) по возмущающему воздействию:
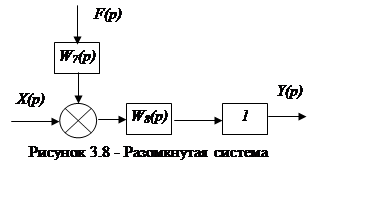 |
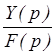 =
= 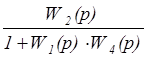 =
= 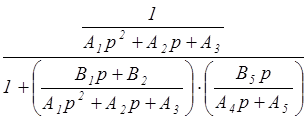 =
=
=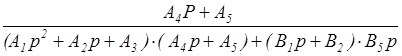 =
=
= 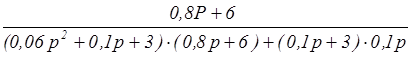 =
= 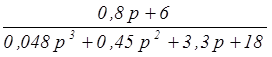 ;
;
Передаточная функция разомкнутой системы (рисунок 3.8) по задающему воздействию:
F(P) = 0;
WXY(p) = 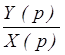 =
=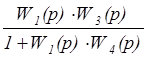 =
=
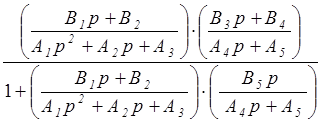 =
=
= 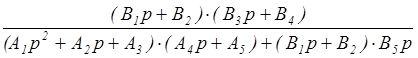 =
=
= 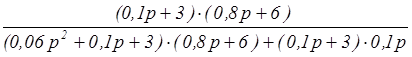 =
= 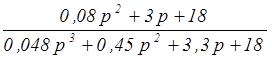 ;
;
WразXY (0) =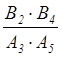 =
18/18 = 1.
=
18/18 = 1.
Используя данные задания 1, построить амплитудно-фазовую (АФЧХ), амплитудную (АЧХ) и фазовую (ФЧХ) частотные характеристики системы.
Общий вид уравнения передаточной функции разомкнутой системы по задающему воздействию:
WXY(p) = 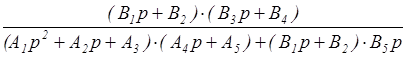 ;
;
WXY(p) = 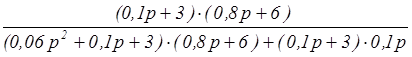 ;
;
Получим АФЧХ путем замены р в передаточной функции на jw.
Получим комплекснозначную функцию:
W(jw)=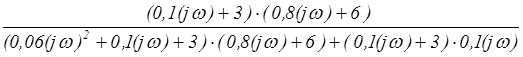 =
= 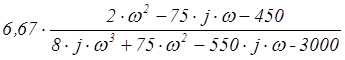 =
= 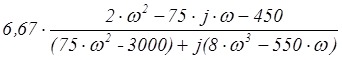 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.