Установление вещества по его рентгенограмме и расчёт параметров кристаллической ячейки: Методические указания к лабораторной работе № 1, страница 3

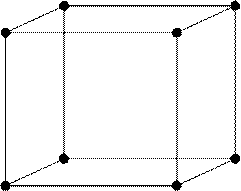
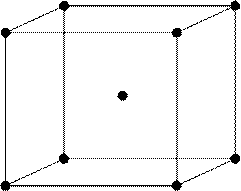
В каждой сингонии решетки делятся по степени заполнения их атомами. Например, для кубической сингонии наблюдается три ячейки: простая кубическая - на ячейку приходится один атом; объемоцентрированная кубическая (ОЦК) - на ячейку приходится два атома; гранецентрированная кубическая (ГЦК) - на ячейку приходится четыре атома (рис.5).  Все известные в природе кристаллические тела имеют одну из 14 ячеек (так называемых решеток Браве), которые отличаются друг от друга типом симметрии и степенью заполнения ячеек атомами.

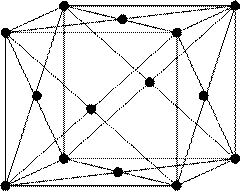              простая кубическая                        ОЦК                                      ГЦК

Рис.5. Кубические ячейки

Индецирование рентгенограммы. Операцию определения индексов (HKL) каждому рефлексу рентгенограммы называют индецированием [5]. Исходной формулой для определения миллеровских индексов отражающих плоскостей является формула закона Вульфа-Брэггов: 2d_НКL sinq = nl. Каждому значению sinq, а следовательно, и d_НКL,  соответствуют определенные значения миллеровских индексов (HKL) отражающих плоскостей. Обратное предположение справедливо только для некоторых простых решеток. В случае сложных решеток некоторые отражения гасятся и отсутствуют на рентгенограммах.

Индексы  первых семи линий рентгенограммы кубических решеток приведены в табл 4.

                                                                                                             Таблица 4

Из квадратичной формы для кубической сингонии

                                   Sin²q = l²(Н²+К²+L²) / 4 a²

следует, что отношение синусов углов отражения для разных линий рентгенограммы должны быть равны соответствующему отношению сумм квадратов индексов, следовательно, отношению целых чисел.

                     Sin²q_i / Sin²q_m = (H_i²  + K_i² + L_i²) / (H_m²  + K_m² + L_m²) = B.

Если в знаменателе взять m = 1, то ряд отношений для всех линий рентгенограммы в порядке возрастания углов дифракции должен представлять собой строго определенный ряд чисел B_i, различный для решеток разного типа (табл. 5).

                                                                                                                    Таблица 5

Ряд B для кубических решеток

Задача индецирования  сводится к тому, чтобы найти значения Sin²q для всех линий рентгенограммы и ряд отношений Sin²q_i / Sin²q₁ = B_i , который сопоставляется с рядами табл.5. Этим сравнением определяется тип решетки исследуемого вещества. Затем, используя данные табл.4, следует присвоить индексы отражающих плоскостей всем линиям рентгенограммы.

Определение размеров элементарной ячейки. После индецирования рентгенограммы вещества с кубической решеткой период последней легко определяется по формуле:

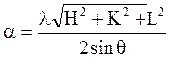                                          ,                                 (2)

где l - длина волны рентгеновского излучения.

Порядок расчета рентгенограммы

1. Продолжить расчёт рентгенограммы вещества. Результаты расчетов дифракционных углов 2q  и q  из табл. 2 перенести занести в табл. 6.

2. Найти экспериментальный ряд чисел B_i, равный отношению Sin²q_i каждой линии к Sin²q₁ первой линии. Сравнить полученный ряд чисел с табличными рядами, представленными в табл.5. Этим сравнением определяется тип элементарной ячейки.