Установление вещества по его рентгенограмме и расчёт параметров кристаллической ячейки: Методические указания к лабораторной работе № 1

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Лабораторная работа № 1

УСТАНОВЛЕНИЕ ВЕЩЕСТВА ПО ЕГО РЕНТГЕНОГРАММЕ И РАСЧЁТ ПАРАМЕТРОВ КРИСТАЛЛИЧЕСКОЙ ЯЧЕЙКИ

Цель работы: рассчитать рентгенограмму от неизвестного вещества, определить тип вещества и тип кристаллической ячейки, рассчитать параметры кристаллической ячейки

Приборы: рентгенограмма.

Часть 1. УСТАНОВЛЕНИЕ ВЕЩЕСТВА ПО ЕГО РЕНТГЕНОГРАММЕ

Краткая теория

Любое кристаллическое вещество характеризуется упорядоченным расположением частиц (атомов, атомных остатков, молекул) по объему. В естественных условиях кристаллы встречаются в виде поликристаллов. В нихправильная периодичность в расположении частиц наблюдается в небольших объемах, называемых монокристаллами.

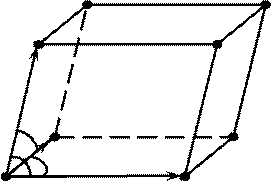
При описании правильной кристаллической структуры обычно используют понятие кристаллической решетки. Она представляет собой пространственную сетку, в узлах которой расположены частицы. В основе кристаллической решетки лежит элементарная ячейка, представляющая собой параллелепипед с характерным для данной решетки расположением частиц (рис.1). Расстояние между однородными атомами в элементарной ячейке называют периодом или постоянной кристаллической решетки. Периоды кристаллических решеток всех простых веществ имеют порядок нескольких нанометров.

Через узлы кристаллической решетки можно провести прямые линии и плоскости. Одинаково ориентированные в пространстве они представляют собой семейства прямых и плоскостей, которые кристаллографически идентичны и обладают одинаковыми расстояниями между собой. Знание межплоскостных расстояний позволяет охарактеризовать кристаллическуюрешетку исследуемого объекта и установить тип вещества или отдельной фазы, если соединение сложное по составу. Данные о межплоскостных расстояниях для различных веществ и фаз можно найти в специальных таблицах и справочной литературе по рентгеноструктурному анализу. Определение фазового состава поликристаллических веществ по их межплоскостным расстояниям является одной из наиболее распространенных задач рентгеноструктурного анализа.

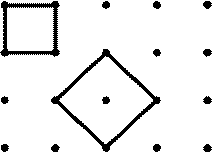
Ориентировка семейства плоскостей (прямых, узлов) в решетке однозначно определяется кристаллографическими индексами (их называют миллеровскими индексами). Под миллеровскими индексами плоскости понимают три взаимно простых целых числа Н, К, L, которые представляют собой дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых любой плоскостью данного семейства на координатных осях. Совокупность индексов плоскости, взятая в круглые скобки, называется символом плоскости - (НКL). Важнейшие плоскости в кубической решетке и их индексы показаны на рис. 2.

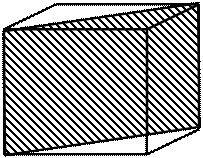
Для рентгеновских лучей кристаллы являются естественными дифракционными решетками. Дифракцию лучей на кристаллах можно представить как рассеяние их кристаллографическими плоскостями решетки (рис.3). В направлении угла дифракции q наблюдается максимум интенсивности лучей, отраженных плоскостями одного семейства, если соблюдается закон Вульфа-Брэггов:

                               2d_НКL sinq = nl,                                                                 (1)

где d_HKL - межплоскостное расстояние, l - длина волны характеристического рентгеновского излучения, n - порядок максимума.

Подставляя в формулу (1) значения d_HKL для разных решеток, получают для них соответствующие равенства, называемые квадратичными формами. В качестве  примера квадратичные формы для некоторых решеток приведены в табл. 1.

                                                                                                         Таблица 1

Примечание: в таблице величины а и с - параметры кристаллической ячейки.

Порядок выполнения работы

1.  Получить у преподавателя номер рентгенограммы вещества, расчет которой нужно сделать. Внешний вид заданной рентгенограммы приведен в приложении на стр.10-11. Рентгенограммы получены на рентгеновском дифрактометре ДРОН-3 в медном фильтрованном излучении с длиной волны l = 0,154 нм. Рентгенограмма простых веществ имеет четкий набор дифракционных максимумов, расположенных под разными углами 2q и имеющих разную интенсивность (рис.4).

                                                                            c

                                                                               g

                                                                         bb

                                                                                  a

 а) плоские ячейки                                                                 a           

                                                                       б) пространственная ячейка

Рис. 1. Кристаллическая ячейка

         (100)                                         (110)                                         (111)      

Рис. 2. Основные плоскости кубической ячейки

Рис. 3.  Рассеяние рентгеновских лучей плоскостями кристаллической решетки

Рис.4. Внешний вид рентгенограммы

2.  Каждой дифракционной линии рентгенограммы присвоить номер по порядку в порядке возрастания углов 2q, начиная с наименьших углов дифракции. Произвести оценку интенсивности линий на глаз по пятибальной системе:

                                очень сильная         О.С.               100 %         (1.00)