Исследование метода оптимального обнаружения сигнала на фоне флуктуационного шума, страница 2

На основе анализа апостериорных вероятностей приемник должен выдать в качестве решения одну из указанных выше гипотез и отбросить другую. Естественно считать, что решение о наличии или отсутствии сигнала должно приниматься путем сравнения апостериорных вероятностей по определенному правилу. Другими словами, должно приниматься более вероятное решение. Для этого используется неравенство

.                                             (4.1)

Величина Λ характеризует правдоподобность той или иной гипотезы. При Λ > 1 полагается, что гипотеза «» правдоподобнее гипотезы «», поэтому величину Λ называют отношением правдоподобия.

Правило выбора гипотез по критерию максимума апостериорной вероятности называется байесовским правилом или байесовским решением. Оно автоматически обеспечивает минимизацию вероятности ошибки при выборе гипотезы и, следовательно, является наиболее разумным правилом при оценке качества передачи информации по каналу связи.

Известно, что алгоритм работы оптимального приемника сводится к проверке следующего неравенства:

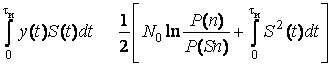 ,                              (4.2)

где  – мощность шума, приходящаяся на единицу полосы частот.

Правую часть выражения (4.2) можно вычислить до приема и, заменив ее некоторой константой , в дальнейшем работать с ней как с порогом:

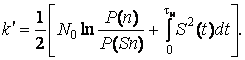                             (4.3)

Тогда

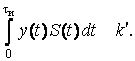                                                          (4.4)

Если интеграл в левой части неравенства (4.4) превысит порог k', то регистрирующее устройство приемника отметит наличие сигнала, в противном случае – его отсутствие. В этом неравенстве известны: интервал времени t_и , в котором производится наблюдение за принятой реализацией; передаваемый сигнал S(t); его форма, амплитуда, частота и фаза; порог k'. Неизвестным членом является лишь реализация y(t), которую может принять приемник. Однако эта неизвестность устраняется вместе с принятием какой-либо конкретной реализации.