Примеры решения задач по теме № 5 «Физика колебаний и волн»

Примеры решения задач по теме 5

«Физика колебаний и волн»

          Задача 1 Материальная точка массой m=5 г совершает гармонические колебания с частотой n=0,5 Гц. Амплитуда А=3 см. Определить: а) Скорость точки в момент времени, когда смещение х=1,5 см; б) максимальную силу F_max, действующую на эту точку; в) полную энергию Е колеблющейся точки.

Дано:                                               Решение

m=1 г                    1. Уравнение гармонического колебания имеет вид

n=0,5 Гц                                       х=Аcos(wt+j).                                                              (1)

А=3 см                                              

x=1,5 см               Для нахождения скорости точки возьмем первую производную

                              по времени от смещения:

u, F_max, E - ?                           u=dx/dt=-Awsin(wt+j).                                                      (2)

Чтобы выразить скорость через смещение, нужно исключить время из формул (1) и (2). Для этого возведем оба уравнения в квадрат, разделим первое на А², второе на А²w² и сложим:

                                                       x²/A²+u²/(A²w²)=1;

                                            w=2pn Þ x²/A² + u²/(A²4p²n²) = 1

Найдем выражение для скорости точки

                                          u²=A²4p²n²(1 - x²/A²) = 4p²n²(A² - x²)

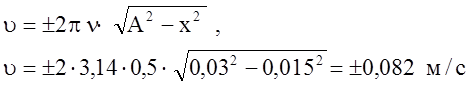
Знак плюс соответствует направлению вектора скорости, совпадающему с положительным направлением оси x, знак минус – с отрицательным.

2. Силу, действующую на точку, найдем по второму закону Ньютона 

                                                                 F=ma,                                                                 (3)

где a - ускорение точки, которое можно получить, взяв производную по времени от скорости:

                                    а=du/dt=-Aw²cos(wt+j)=-4p²n²Acos(wt+j),

                                                  F=-4p²n²mAcos(wt+j).

Максимальное значение  силы будет при cos(wt+j)=-1 Þ

                                                 F_max=4p²n²mA ,

                                       F_max=4×3,14²×0,5²×0,005×0,03=1,49 мН

3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. W=W_k+W_п. В соответствии с законом сохранения полной механической энергии в момент, когда кинетическая энергия достигает максимального значения, потенциальная энергия равна нулю. Поэтому полная энергия W колеблющейся точки равна максимальной кинетической энергии W_{k max}:

                                                   W=W_{k max}=mu²_max /2.                                                       (4)

Максимальную скорость найдем из уравнения (2) при sin(wt+j)=-1;

                                                         u_max=2pnA.                                                                (5)

Подставим (5) в (4): W=2p²mn²A²

                                  W=2×3,14²×0,005×0,5²×0,03²=22,1 мкДж.

Ответ:u = ±0,082 м/с; F_max= 1,49 мН; W= 22,1 мкДж.

Задача 2 Гиря массой 0,5 кг подвешена к пружине, жесткость  которой   k=32,0 Н/м и совершает затухающие колебания. Определить их период, если за время двух колебаний (N=2) амплитуда уменьшилась в h=20 раз. Какова добротность данного осциллятора, если под действием вынуждающей вертикальной гармонической силы с частотой W=10 с^-1 гиря будет совершать установившиеся колебания. При этом смещение гири будет отставать по фазе от вынуждающей силы на j=3p/4.

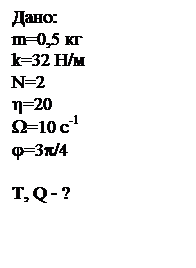
                                      Решение

В данной задаче следует рассмотреть два случая

1. Сопротивление среды уменьшает частоту свободных колебаний, что приводит к их затуханию.

2. Под действием вынуждающей силы гиря совершает установившиеся гармонические колебания.

Решим первую задачу.

Период затухающих колебаний может быть найден через циклическую частоту затухающих колебаний w:

                                           ,           

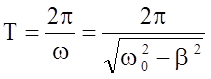где w₀ - собственная циклическая частота, b - коэффициент затухания.

                                                ,     

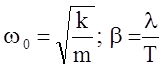где l - логарифмический декремент затухания.

                                                .

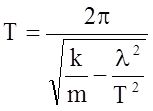Выразим период колебаний     

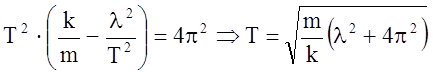                             .                                   (1)

Закон убывания амплитуды затухающих колебаний: А=А₀e^-bt=A₀e^{-lt / T}. По условию А₀/А=h. Число колебаний N=t/T, где t - общее время колебаний, T - время одного колебания (период). A₀/A=e^lN=h. Логарифмируя, получим

                                                     l = ln(h)/N.                                                                  (2)

Подставим выражение (2) в (1): 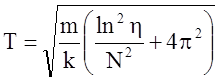. Подставив числовые значения, получим T=0,81 c.

Во втором случае  на гирю будет действовать вынуждающая сила, изменяющаяся по гармоническому закону   F=F₀cos Wt.

Тогда (с учетом отставания по фазе на j=3p/4) гиря будет совершать установившиеся вынужденные колебания по закону   x(t)=Acos