Примеры решения задач по теме № 6 «Квантовая физика»

Определить, какие спектральные линии появятся в спектре атома водорода.

                                    Решение

     При возбуждении атома электрон в атоме переходит из основного состояния (m=1) в состояние с главным квантовым числом n, которое можно определить по формуле:

          1/l=R(1/m² - 1/n²) .

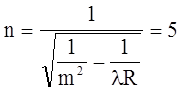                                            (округляем до меньшего целого).

Таким образом, при обратном переходе с 5-го уровня электроны могут переходить на 1, 2, 3, 4-й уровни. Этим переходом будут соответствовать определенные спектральные линии:

Всего будет наблюдаться 10 линий:

4 линии в серии Лаймана;

3 - в серии Бальмера;

2 - в серии Пашена;

1 - в серии Брэккета.

          Ответ: n = 10.

Задача 5 Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=0,5 кВ. Принимая, что неопределенность импульса равна 0,1 % от его численного значения, найти неопределенность координаты электрона. Являются ли в данных условиях электроны квантовыми или классическими частицами?

Дано: U = 0,5 кВ Dpx=0,001px

Dx - ?

                                Решение

 Согласно соотношению неопределенностей

                               DxDp_x ³ h,                                            (1)

где Dx - неопределенность   координаты электрона;       Dp_x - неопределенность проекции его импульса; h=6,63×10^-34 Дж×с - постоянная Планка. Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U:

                                                            T = |e|U = 0,5 кэВ,

то есть электрон при данных условиях не является релятивистской частицей, и импульс электрона

                                        

Согласно условию задачи, неопределенность импульса Dp_x=0,001p_x=1,24×10^-26 кг×м/с, то есть Dp_x=0,001p_x=1,24×10^-26 кг×м/с, то есть Dp_x<<p_x, и электрон при данных условиях является классической частицей.

Искомая неопределенность координаты из выражения (1)

                                        .

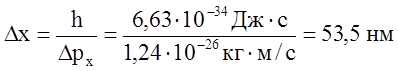          Ответ: Dx = 53,5 нм.

          Задача 6  Электрон в одномерной прямоугольной «потенциальной яме» шириной l = 200 пм с бесконечно высокими «стенками» находится  в  возбужденном  состоянии  (n = 4).  Определить:  1) минимальную энергию электрона; 2) вероятность W обнаружения электрона в первой четверти «ямы».

    

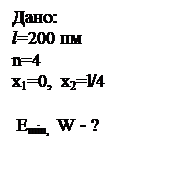
                                         Решение

     Собственное значение энергии электрона, находящегося на n-м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»:

                                          ,

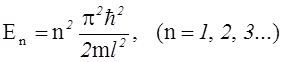где m=9,1×10^-31 кг - масса электрона; 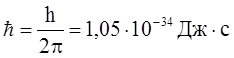  - постоянная Планка.

Минимальную энергию электрон имеет при минимальном n, то есть при n = 1:

                        .

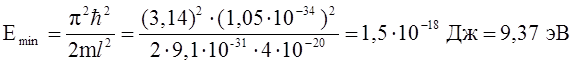Вероятность обнаружить частицу в интервале x₁<x<x₂:

                                                  

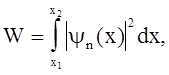
где 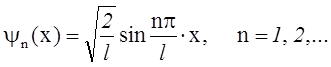  -  нормированная собственная волновая функция, соответствующая данному состоянию.

Возбужденному  состоянию n=4 отвечает собственная функция

                                                   .

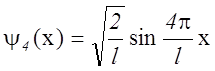Тогда по условию задачи,

                             .

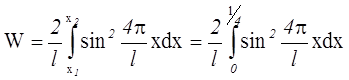Заменив sin²(4px/l)=1/2×(1-cos(8px/l)), запишем

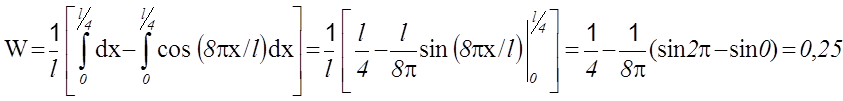
График зависимости

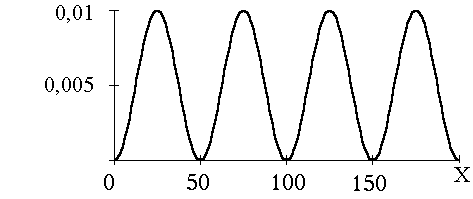
          Ответ: E_min, = 9,37 эВ; W = 0,25.

          Задача 7 Первоначальная масса радиоактивного изотопа радона  (период полураспада T_1/2=3,82 сут.) равна 1,5 г.   Определить:   1) начальную активность изотопа;   2) его активность через 5 суток.

Дано:                                                             m0=1,5 г T1/2=3,82 сут t=5 сут

A0 , A - ?

                              Решение

Начальная активность изотопа

                               A₀=lN₀,

где 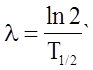- постоянная радиоактивного распада;              N₀ -число ядер изотопа в начальный момент времени.

                        ,

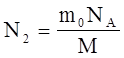где M - молярная масса радона (M=222×10^-3 кг/моль); N_A - число Авогадро, равное 6,02×10²³ моль^-1. Учитывая это выражение, найдем искомую начальную активность изотопа

                                           

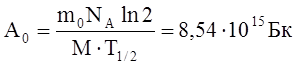
Активность изотопа A=lN, где, согласно закону радиоактивного распада, N=N₀e^-lt - число нераспавшихся ядер в момент времени t. Учитывая  lN₀=A₀, найдем, что активность нуклида уменьшается со временем по закону:

                                          A=A₀e^-lt=.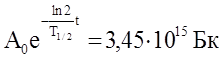

          Ответ: A₀ = 8,54×10¹⁵ Бк; A = 3,45×10¹⁵ Бк.

          Задача 8 В результате соударения дейтрона с ядром бериллия  образовалось новое ядро и нейтрон. Определить порядковый номер и массовое число образовавшегося ядра, записать ядерную реакцию и определить ее энергетический эффект.

Дано:

Z, A, Q - ?

                                             Решение

Из законов сохранения электрического заряда и массовых чисел следует, что Z=5, A=10, то есть образовавшееся в результате ядерной реакции ядро - изотоп бора . Поэтому ядерную

реакцию можно записать в виде

                                                         

Энергетический эффект реакции

                                        ,                               

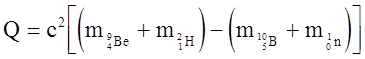где в первых круглых скобках указаны масса исходных ядер, во вторых