2. Вероятность того, что на странице книги имеется опечатка, равна 0,2. Какова вероятность наличия опечаток в главе, содержащей 4 страницы?
Решение
Пусть
А — наличие опечаток в главе (т.е. имеется хотя бы одна опечатка). Применим
формулу для вероятности хотя бы одного события: ![]()
Ответ: 0,5904.
1. Студент выучил 15 вопросов из 17. Какова вероятность того, что он знает все три вопроса, входящие в билет? Знает два из них?
Решение
Применим формулу классической вероятности. При выборе 3 объектов из 17 данных общее число исходов
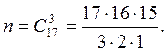
а)
Событие А (знает все три вопроса): 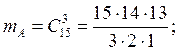
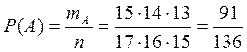 .
.
б)
Событие В (знает два вопроса): 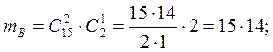
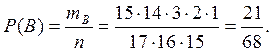
Ответ: 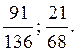
3. Из всех новорожденных доживают до 60 лет 40% мальчиков и 65% девочек. Какая часть всех новорожденных доживет до 60 лет, если вероятность рождения мальчика равна 0,52?
Решение
Рассмотрим событие В — «новорожденный дожил до 60 лет». По условию, вероятность этого события зависит от следующих гипотез.
А1
— новорожденный является мальчиком. ![]()
А2
— новорожденный является девочкой. ![]() (сумма вероятностей
всех гипотез равна 1).
(сумма вероятностей
всех гипотез равна 1).
По
условию, ![]()
![]()
Вычислим
по формуле полной вероятности: ![]()
![]()
Ответ: 49,6%.
3. Из урны, содержащей 3 красных, 5 синих и 2 белых шара, извлекли одновременно два шара. Какова вероятность того, что они — разного цвета?
Решение
Пусть
событие А —«шары разного цвета», тогда противоположное событие ![]() — «шары одного цвета», то есть В1
— «оба красные», или В2 — «оба синие», В3 — «оба белые».
Вычислим вероятности трех последних событий:
— «шары одного цвета», то есть В1
— «оба красные», или В2 — «оба синие», В3 — «оба белые».
Вычислим вероятности трех последних событий:
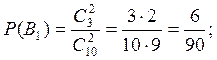
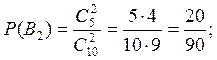
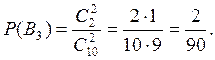 По формуле сложения вероятностей
По формуле сложения вероятностей 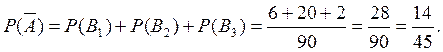
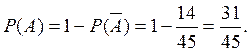 Ответ:
Ответ: ![]()
1. Телефонный номер состоит из шести цифр (первая — не ноль). Найти вероятность того, что все цифры разные.
Решение
Применим
формулу классической вероятности. Т.к. первая цифра не может быть нулем (всего
9 возможностей, а остальные 5 цифр могут быть любыми), то общее число возможных
исходов ![]() .
.
Найдем число исходов, благоприятных для события А— «все цифры разные»:
![]() (первая цифра любая, кроме нуля, вторая
любая, кроме первой, третья любая, кроме первой и второй, и т.д.).
(первая цифра любая, кроме нуля, вторая
любая, кроме первой, третья любая, кроме первой и второй, и т.д.).
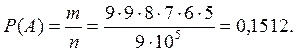 Ответ: 0,1512.
Ответ: 0,1512.
1. Телефонный номер состоит из шести цифр (первая — не ноль). Найти вероятность того, что номер содержит двойку.
Решение
Применим
формулу классической вероятности. Т.к. первая цифра не может быть нулем (всего
9 возможностей, а остальные 5 цифр могут быть любыми), то общее число возможных
исходов ![]() .
.
Найдем число исходов, благоприятных для события А— «номер не содержит двойки»:
![]() (первая цифра любая, кроме нуля и двойки,
остальные любые, кроме двойки).
(первая цифра любая, кроме нуля и двойки,
остальные любые, кроме двойки).
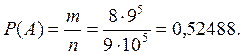
Требуется
найти вероятность противоположного события ![]() —
«номер содержит хотя бы одну двойку».
—
«номер содержит хотя бы одну двойку».
![]()
Ответ:
![]()
3. Что вероятнее: хотя бы 4 орла при пяти бросаниях монеты или ровно 1 орел при четырех?
Решение
Вычислим обе вероятности, применяя формулу Бернулли.
а) 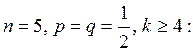
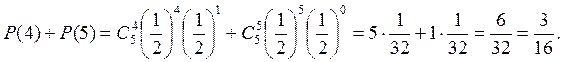
б) 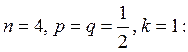
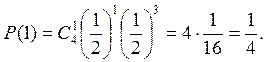
Вторая вероятность больше.
Ответ: вероятнее один орел при четырех бросаниях монеты.
1. Телефонный номер состоит из шести цифр (первая — не ноль). Найти вероятности того, что номер содержит только цифры 1 и 2.
Решение
Применим
формулу классической вероятности. Т.к. первая цифра не может быть нулем (всего
9 возможностей, а остальные 5 цифр могут быть любыми), то общее число возможных
исходов ![]() .
.
Найдем число исходов, благоприятных для события А— «номер содержит только цифры 1 и 2»:
![]() (для каждой из шести цифр две
возможности).
(для каждой из шести цифр две
возможности).
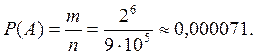 Ответ:
Ответ: ![]()
2. Шахматист А выигрывает у Б белыми с вероятностью 0,5, черными — с вероятностью 0,2, вероятность ничьей в обоих случаях равна 0,4. Играются две партии (со сменой цвета). Какова вероятность ничейного счета после двух партий?
Решение
Ничейный счет достигается в следующих трех случаях.
а)
А выиграл первую партию (белыми) и проиграл вторую (черными). Соответствующие
вероятности, по условию, равны 0,5 и 1-0,2-0,4=0,4. Применим формулу умножения
вероятностей независимых событий:![]() .
.
б)
А проиграл первую партию и выиграл вторую (вероятности 1-0,5-0,4=0,1 и 0,2). ![]()
в)
В обеих партиях ничьи. ![]()
Применим
формулу сложения вероятностей несовместных событий: искомая вероятность равна ![]()
Ответ: 0,38.
3. Известно, что в июне бывает в среднем 30% дождливых дней, в июле — 18%, в августе — 24%. Найти вероятность дождя в произвольно выбранный летний день.
Решение
При случайном выборе летнего дня возможны три гипотезы.
А1
— выбран день в июне. 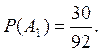 А2 — выбран
день в июле.
А2 — выбран
день в июле. 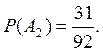 А3 — выбран день в
августе.
А3 — выбран день в
августе. 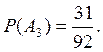
Пусть
событие В — дождь в выбранный день. По условию, ![]()
![]()
![]()
Вычислим
по формуле полной вероятности: ![]()
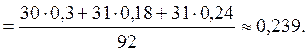
Ответ:
![]()
1. Какова вероятность, расставляя в случайном порядке карточки с буквами А,А,Г,М,М, получить слово ГАММА?
Решение
Применим формулу классический вероятности.
Число
способов переставить 5 карточек равно ![]()
Число
благоприятных перестановок равно ![]() так как буквы А и М
каждая допускают по 2 перестановки, а буква Г занимает единственное положение.
так как буквы А и М
каждая допускают по 2 перестановки, а буква Г занимает единственное положение.
Искомая
вероятность равна 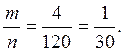 Ответ:
Ответ: ![]()
3. Из всех телевизоров, выпускаемых заводом «Изумруд», 20% — черно-белые. Известно, что гарантийный ремонт требуется каждому четвертому из черно-белых телевизоров и каждому третьему цветному. Какая часть всей продукции подлежит гарантийному ремонту?
Решение
Так как по условию вероятность гарантийного ремонта зависит от типа телевизора, то применим формулу полной вероятности. Рассмотрим 2 гипотезы:
А1
— выбранный телевизор — черно-белый. По условию, ![]()
А2
— выбранный телевизор — цветной. ![]()
Пусть
событие В состоит в том, что выбранный телевизор потребовал гарантийного
ремонта. По условию, 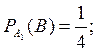
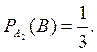
Вычислим
по формуле: 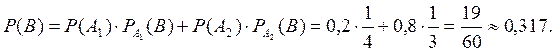
Ответ:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.