1. Из урны, содержащей 3 красных, 2 синих и 1 белый шар, извлекли одновременно три шара. Какова вероятность того, что они разного цвета?
Решение
Применим формулу классической вероятности.
При
извлечении 3 шаров из 6 имеющихся общее число возможных исходов 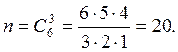
Число
благоприятных исходов ![]() (любой из трех красных, любой из
двух синих, единственный белый шар).
(любой из трех красных, любой из
двух синих, единственный белый шар).
Искомая
вероятность равна 
Ответ: 0,3.
2. В институте из 600 студентов 50 отличников. Найти вероятность наличия отличников среди выбранных наугад трех студентов
Решение
Пусть
событие А — наличие (хотя бы одного) отличника среди выбранных студентов. Тогда
противоположное событие ![]() — среди выбранных нет
отличников.
— среди выбранных нет
отличников.
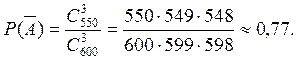
![]()
Ответ:
![]()
2. При стрельбе по тарелочке можно сделать три выстрела; вероятности попадания равны соответственно 0,7; 0,4; 0,2. Найти вероятность того, что тарелочка будет разбита.
Решение
Применим
формулу для вычисления вероятности хотя бы одного из нескольких независимых
событий. Искомая вероятность равна ![]()
Ответ: 0,856.
3. Вероятность рождения мальчика равна 0,52. В семье четверо детей. Найти вероятности того, что в ней:
а) двое мальчиков;
б) хотя бы двое мальчиков.
Решение
Применим формулу Бернулли.
Дано:
![]() ,
, ![]()
а) ![]()
б)Требуется вычислить вероятность не менее 2 успехов.
![]()
Ответ: 0,3738; 0,7169.
1. Рассеянный профессор разложил три письма по трем конвертам случайным образом. Найти вероятность того, что хотя бы одно письмо дойдет по назначению.
Решение
Пусть конверты лежат в порядке 1, 2, 3.
Письма
можно разложить 6-ю вариантами (число перестановок трех элементов ![]() ).
).
Благоприятными
считаем варианты, когда хотя бы одно письмо попадет в конверт с тем же номером.
Перечислим благоприятные варианты: 1,2,3; 1,3,2; 2,1,3; 3,2,1 (всего ![]() варианта).
варианта).
Искомая
вероятность равна 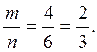 Ответ:
Ответ: ![]()
2. При стрельбе по тарелочке можно сделать три выстрела; вероятности попадания равны соответственно 0,7; 0,4; 0,2. Найти вероятность того, что тарелочка будет разбита вторым или третьим выстрелом.
Решение
Рассмотрим следующие события:
А
— попадание при первом выстреле, по условию, ![]()
В —
попадание при втором выстреле, по условию, ![]()
С —
попадание при третьем выстреле, по условию, ![]()
Вероятность попадания при втором или третьем выстреле вычислим по формуле сложения вероятностей.
Первое
попадание при втором выстреле: ![]()
Первое
попадание при третьем выстреле: ![]()
Ответ:
![]()
1. Из монет в 50 копеек, 1, 2, 2 и 5 рублей потерялись две. Какова вероятность того, что потерянная сумма превосходит 3 рубля?
Решение
Применим формулу классической вероятности.
При
извлечении 2 объектов из 5 имеющихся общее число возможных исходов 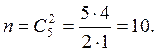
Перечислим исходы, благоприятные для события А: «сумма превосходит 3 рубля».
0,5+5,
1+5, 2+2, 2+5, 2+5 (всего ![]() исходов).
исходов).
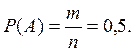
Ответ: 0,5.
2. Вероятность поломки станка за день равна 0,1. Какова вероятность того, что за рабочую неделю (5 дней) не будет ни одной поломки?
Решение
Вероятность
того, что станок проработает день без поломок, равна ![]()
Для
вычисления вероятности отсутствия поломок за 5 дней применим правило умножения
вероятностей независимых событий: ![]()
Ответ:
![]()
3. Завод «Изумруд» получает кинескопы с двух других заводов, причем первый из них обеспечивает 60% потребности. Какой процент кинескопов выдерживает три года работы, если для кинескопов первого завода вероятность этого равна 0,7, а для кинескопов второго — 0,85?
Решение
Применим формулу полной вероятности. Для случайно выбранного кинескопа рассмотрим 2 гипотезы
А1
— кинескоп произведен первым заводом. По условию, ![]()
А2
— кинескоп произведен вторым заводом. ![]()
Пусть
событие В состоит в том, что кинескоп выдержал три года работы. По условию, ![]()
![]()
Вычислим
по формуле: ![]()
Ответ: 76%.
1. В вагоне, содержащем 10 купе по 4 места, оказались двое знакомых. Найти вероятность того, что их места в одном купе.
Решение
Применим формулу классической вероятности. Второй из знакомых может с равной вероятностью занимать любое из n=39 мест (за исключением того места, которое занял первый). Из них m=3 места находятся в том же купе.
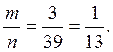 Ответ:
Ответ: ![]()
2. Слово КОЛОКОЛ разрезали на 7 букв, их перемешали и выложили в ряд три буквы. Найти вероятность того, что получили слово КОЛ.
Решение
Рассмотрим следующие события:
А — первой оказалась буква К,
В — второй оказалась буква О,
С — третьей оказалась буква Л.
Применим формулу умножения вероятностей зависимых событий:
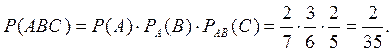 Ответ:
Ответ: ![]()
1. Фишки с номерами 1,2,3,4,5,6,7,8 расставлены по кругу случайным образом. Найти вероятность того, что фишки 1 и 2 оказались рядом
Решение
Применим формулу классической вероятности.
Пусть
фишка 1 заняла определенное место. Для фишки 2 существует ![]() равновозможных исходов (мест), из них
равновозможных исходов (мест), из них ![]() благоприятных для события А — «фишка 2
находится рядом с фишкой 1».
благоприятных для события А — «фишка 2
находится рядом с фишкой 1».
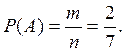 Ответ:
Ответ: ![]()
2. Слово КОЛОКОЛ разрезали на 7 букв, их перемешали и выложили в ряд три буквы. Найти вероятность того, что получили слово ОКО.
Решение
Рассмотрим следующие события:
А — первой оказалась буква О,
В — второй оказалась буква К,
С — третьей оказалась буква О.
Применим формулу умножения вероятностей зависимых событий:
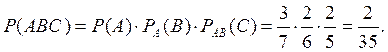
Ответ:
![]()
2. Из колоды в 36 карт извлечены наугад три. Найти вероятность того, что они — разных мастей.
Решение
Рассмотрим следующие события.
А —
вторая карта не той же масти, что первая. 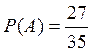 (из 35
оставшихся карт 27 имеют другую масть).
(из 35
оставшихся карт 27 имеют другую масть).
В —
третья карта не той же масти, что первая или вторая. 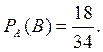
Применим
формулу умножения вероятностей зависимых событий: 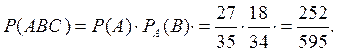
Ответ:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.