2009-09-29
Лекция 6
Метод последовательного улучшения решения (продолжение)
Для нахождения
оптимального решения, подставим 2 в минимизированную линейную функцию ![]() , выраженную через свободные переменные.
Тогда получим форму записи 4:
, выраженную через свободные переменные.
Тогда получим форму записи 4:
![]() (4)
(4)
Подставим 2 в 4 и получим форму записи 5:
![]() (5)
(5)
Вопрос: можно
ли улучшить решение, уменьшить функцию L, увеличивая
переменные ![]() :
:
а) если все
коэффициенты ![]() в уравнении 4 положительны, то увеличивать
коэффициенты
в уравнении 4 положительны, то увеличивать
коэффициенты ![]() нельзя, так как L будет возрастать, а мы эту функцию минимизируем.
Следовательно, найденное решение не будет оптимальным;
нельзя, так как L будет возрастать, а мы эту функцию минимизируем.
Следовательно, найденное решение не будет оптимальным;
б) если среди
коэффициентов ![]() есть отрицательные, то,
увеличивая переменные при отрицательных коэффициентах, решение улучшить можно,
уменьшив L.
есть отрицательные, то,
увеличивая переменные при отрицательных коэффициентах, решение улучшить можно,
уменьшив L.
В некоторых уравнениях системы 1 коэффициенты перед x отрицательны. Выберем из них то уравнение, в котором отношение свободного члена к отрицательному коэффициенту наименьшее по модулю.
![]() (6)
(6)
где ![]()
Из выражения 6 видно,
что при подстановке в него 2, переменная ![]() остается
неотрицательной только при
остается
неотрицательной только при 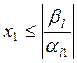 .
.
Далее нужно
переразрешить систему уравнений 1, вводя в число свободных переменных,
переменную ![]() . А бывшую свободную переменную
. А бывшую свободную переменную ![]() перевести в базисные. Аналогично
переразрешается линейная форма 4.
перевести в базисные. Аналогично
переразрешается линейная форма 4.
Вторым шагом решения можно предположить, что все свободные переменные равны нулю. Получим второе опорное решение.
1. Если
все коэффициенты при новой линейной форме ![]() положительны,
то найденное решение оптимально;
положительны,
то найденное решение оптимально;
2. Если среди коэффиентов при переменных новой линейной формы есть отрицательные, то процедура улучшения продолжается.
Пример 1: определить минимум линейной функции
![]() (П_1)
(П_1)
При условиях ограничениях:
![]()
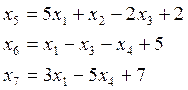 (П_2)
(П_2)
Свободные переменные x1 x2 x3 x4
Базисные переменные – все остальные
1. Пусть свободные переменные равны 0:
![]() (П_3)
(П_3)
Подставим П_3 в П_2. Получим
![]() (П_4)
(П_4)
Подставим П_3 в линейную форму П_1 и получим
L=0 (П_5)
Решение П_3 и П_4 является опорным, так как все свободные члены в П_2 неотрицательны. Решение П_3 и П_4 не является оптимальным, так как в выражении П_1 коэффициент при x3 отрицателен (при уменьшении его, L будет уменьшается).
Переменная x3 входит в 1 и 2 уравнение системы П_2. Причем
коэффициенты перед переменной в обоих уравнениях отрицательны. Из этих двух
уравнений выберем то, в котором отношение свободного члена к отрицательному
коэффициенту перед x3. ![]() (П_6)
(П_6)
Разрешаем уравнение П_6 относительно x3, получаем:
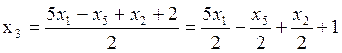 (П_7)
(П_7)
Подставим П_7 во второе уравнение П_2, получаем:
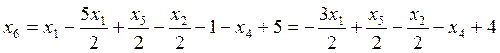 (П_8)
(П_8)
Третье уравнение системы П_2 оставляем без изменений, так там нет x3.
![]() (П_9)
(П_9)
Вывод: привели систему П_2 к системе П_7 – П_9 со свободными переменными x1 x2 x5 x4 и базисные переменные x3 x6 x7.
Выразим линейную функцию через новые свободные переменные. Получим:
![]() (П_10)
(П_10)
2. Пусть все свободные переменные равны нулю.
![]() (П_11)
(П_11)
Подставим П_11 в П_7 – П_9 и получим новое опорное решение:
![]() (П_12)
(П_12)
Подставим П_11 в П-10 и получим:
L = -2 (П_13)
Вывод: второе решение лучше предыдущего, однако не является оптимальным, так как в выражении П_10 коэффициент при x2 отрицателен.
В уравнении П_8 коэффициент перед x2 отрицателен. Поменяем x2 иx6. Тем самым переводим x2 из свободных в базисные переменные. Получаем новую систему:
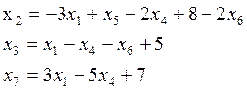
![]() (П_14)
(П_14)
Выразим П_1 через новые свободные переменные:
![]() (П_15)
(П_15)
![]()
3. Все свободные переменные приравняем к нулю:
![]() (П_16)
(П_16)
Подставим П_16 в линейную форму П_15 и получим L = -10. Найденное решение П_17 явялеятся оптимальным, так как коэффициенты при свободных переменных в П_15 являются положительными.
Оптимальное решение определяется подстановкой П_16 в П_14:
![]() (П_17)
(П_17)
Симплекс-метод заключается в переходе от одного допустимого решения к другому путем замены одной группы базисных переменных другой.
Алгоритм нахождения опорного решения
а) если ![]() , причем i пробегает все множество значений, то имеем опорное решение;
, причем i пробегает все множество значений, то имеем опорное решение;
б) если среди ![]() есть отрицательные, то выбираем строку,
соответствующую наибольшему отрицательному свободному члену по модулю.
есть отрицательные, то выбираем строку,
соответствующую наибольшему отрицательному свободному члену по модулю.
2.1
Если все элементы строки ![]() , это означает, что
система уравнений
, это означает, что
система уравнений 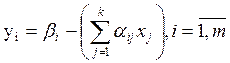 (1)
(1)
не совместима с условием неотрицательности переменных (4):
![]()
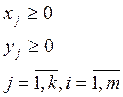 (4)
(4)
2.2 Если в строке имеются отрицательные элементы, то выбираем любой из них.
Пример см. на листе А4.
![]() (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.