Методы решения задач линейного и целочисленного программирования

Приведем заданную модель к каноническому виду, введя свободные переменные y₃ и y₄, превращающие неравенства в равенства. Переменные y₃ и y₄ входят в уравнение с коэффициентом единица и только один раз:

84y₁+84y₂→min

12y₁ + 7y₂ – y₃ = 8

7y₁ + 12y₂ – y₄ = 9

y₃ = – 8 – (–12y₁ – 7y₂)

y₄ = – 9 – (–7y₁ – 12y₂)

Составим симплекс – таблицу:

                За разрешающий элемент мы берем -12, т.к. он находится на пересечении разрешающего столбца и разрешающей строки. Разрешающая строка – это строка с максимальным по модулю отрицательным элементом столбца свободных членов. Разрешающий столбец – столбец, с минимальным симплекс отношением, полученным в результате деления элементов F-строки на элементы разрешающей строки.

                В Разрешающем  столбце, все элементы делятся на разрешающий элемент, меняя при этом знак. В Разрешающей  строчке, все элементы делятся на разрешающий элемент, не меняя при этом знак. А все остальные элементы, находятся по правилу Z.

                План не является оптимальным, т.к. в столбце свободных членов есть отрицательные значения. Значит принимаем за разрешающий элемент -7,91667 и получаем следующую симплекс таблицу:

План является оптимальным, т.к. в столбце свободных членов нетотрицательных элементов.

Ответ:

X₁^*=0,3473

X₂^*=0,5473

F^*=75.1589

6. Математическая постановка задачи линейного целочисленного программирования.

Многие экономические задачи ха­рактеризуются тем, что объемы управляемых ресурсов (в силу тех или иных объективных свойств) могут принимать только целые значения. Математическая формализация данных ситуа­ций приводит к моделям дискретного программирования. В об­щем виде задача дискретного программирования может быть сформулирована как задача нахождения максимума (или мини­мума) целевой функции f(x_l,x₂,...,x_n) на множестве D, опреде­ляемом системой ограничений

                          

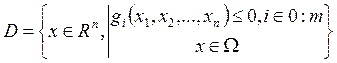
где  — некоторое конечное, или счетное, множество. Ус­ловие  называется условием дискретности. Особое место среди дискретных задач занимает целочисленная за­дача линейного программирования в канонической форме (ЦКЗЛП):

                                                           

                               

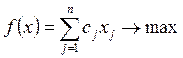
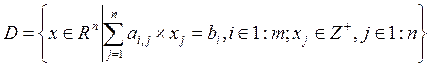
где   Z⁺ ={0; 1; 2; ...} — множество неотрицательных целых чи­сел.

(4)       f=8x₁+9x₂→max

(1)       12x₁+7x₂  ≤ 84

7x₁+12x₂  ≤ 84

(2)       x₁≥0,   x₂≥0

(3)       х₁, х₂ –целые неотрицательные числа.

Найти значения х₁, х_2, удовлетворяющие ограничениям (1) – (3) и доставляющие целевой функции (4) максимальное значение.

7. Дать графическую интерпретацию задачи ЛЦП. Выделить множество допустимых точек. Решить графическим способом задачи ЛЦП.

8x₁+9x₂→max

12x₁+7x₂ ≤ 84

7x₁+12x₂ ≤ 84

x₁≥0,  x₂≥0

Отбрасываем условие целочисленности и решаем графически задачу линейного программирования. Решение приведено в пункте 2.

Оптимальный план - точка В (4,421; 4,421). f(B)= 75,157.

Выделим в области все целочисленные точки, которые являются областью допустимых планов целочисленной задачи.

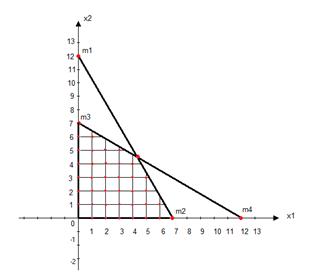
x₂– дробь; подбираем дополнительное ограничение:

≤ 4 

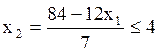
Проверяем точку (5;4)

8*5+9*4 = 40 + 36 = 76 > 75    Данное решение не попадает в ОДР.

Проверяем точку(5;3)

8*5 + 9*3 = 40 + 27 = 67  < 75  => Данное решение является целочисленным решением

Проверяем точку(4;4)

8*4 + 9*4 = 32 + 36 = 68  < 75  => Данное решение является целочисленным решением, и оно более точное.

Ответ:

x₁^*=4

x₂^*=4

F^*=68

8. Решение задачи линейного программирования с помощью метода Гомори.

Решение происходит на основе прямого симплекс метода.

Выбираем свободный член с наибольшей дробной частью.

x₂ = + *x₃ *x₄

Дополнительное ограничение имеет вид

*x₃*x₄ -  ≥ 0

 

Умножим неравенство на -1 и преобразуем его в уравнение. Введем новую переменную х₅

*x₃*x₄  =

х₅ = + *x₃ + *x₄

Составим симплекс-таблицу.

Делаем симплекс преобразование.

Базовые переменные	Свободные члены	Свободные переменные
		x3	X5
X1	7028/1577	11/83	-7/83
X2	6876/1577	-7/83	12/83
X4	40/83	7/83	-95/83
F	118108/1577	25/83	52/83

Так как в Z-строке есть отрицательный элемент,- решаем дальше.

Выбираем свободный член x₄.

x₄ =  *x₃ *x₅

Дополнительное ограничение имеет вид

*x₃*x₅≥ 0

Умножим неравенство на -1 и преобразуем его в уравнение. Введем новую переменную х₆

*x₃*x₅≥ 0

x₆= *x₃*x₅

Составим симплекс-таблицу.

Базовые переменные	Свободные члены	Свободные переменные
		x3	X5
X1	7028/1577	11/83	-7/83
X2	6876/1577	-7/83	12/83
X4	40/83	7/83	-95/83
X6	-40/83	76/83	-12/83
F	118108/1577	25/83	52/83

Делаем симплекс преобразование.

Базовые переменные	Свободные члены	Свободные переменные
		x3	X6
X1	4	2/3	-7/12
X2	3	1	1
X4	1	7/3	-95/12
X5	3	19/3	-83/12
F	72	14	52/12

Так как свободный член F целочисленный (72), то целочисленное решение найдено.

Ответ:

X₁^*=4

X₂^*=3

F^*=72

9. Решение задачи линейного целочисленного программирования с помощью метода ветвей и границ.

(1)       f=8x₁+9x₂→max

 

(2)       12x₁+7x₂≤84           

7x₁+12x₂≤84                                                  

(3)       x₁≥0, x₂≥0

(4)       х₁, х₂ –целые неотрицательные числа.

(5)       0≤ х₁≤5; 0≤ х₂≤5

Снимаем условие целочисленности (4) и решаем задачу1, с условиями 2,3,5

x₁=

x₂=

W=

Ортимальное решение не целочисленно. Вносим в основной список задач 2 задачи.

Задача2: 4≤ х₁≤5; 0≤ х₂≤5; (1), (2), (3)

Задача3: 0≤ х₁≤4; 0≤ х₂≤5

Решаем Задачу2.

При х₁=4,

х₂==

х₂  удовлетворяет условию, следовательно в основной список задач добавляем две задачи:

Задача4:   х₁=4; 0≤ х₂≤3; (1), (2), (3)

Задача5:   х₁=4; 4≤ х₂≤5; (1), (2), (3)

При х₁=5,

х₂==

х₂  удовлетворяет условию, следовательно в основной список задач добавляем две задачи:

Задача6:   х₁=5; 0≤ х₂≤4; (1), (2), (3)

Задача7:   х₁=5; 5≤ х₂≤5; (1), (2), (3)

Решаем Задачу4.

При х₁=4,

х₂==

х₂  не удовлетворяет условию, следовательно решений нет.

Решаем Задачу5.

При х₁=4 и х₂=4,

W=8*4+9*4=68

Решение целочисленно, поэтому запомнаем его.

При х₁=4 и х₂=5,

W=8*4+9*5=77

Решение целочисленно, но больше чем исходное нецелочисленное решение, поэтому не запомнаем его.

Решаем Задачу6.

При х₁=5 и х₂=5,

W=8*5+9*5=85

Решение целочисленно, но больше чем исходное нецелочисленное решение, поэтому не запомнаем его.

Решаем Задачу7.

При х₁=5,

х₂==

х₂  не удовлетворяет условию, следовательно решений нет.

Решаем Задачу3.

При х₁=4,

х₂==

х₂  удовлетворяет условию, следовательно в основной список задач добавляем две задачи:

Задача8:   х₁=4; 0≤ х₂≤3; (1), (2), (3)

Задача9:   х₁=4; 3≤ х₂≤5; (1), (2), (3)

Решаем Задачу8.

При х₁=4,

х₂  не удовлетворяет условию, следовательно решений нет.

Решаем Задачу9.

При х₁=4,

х₂==

х₂  удовлетворяет условию, следовательно в основной список задач добавляем две задачи:

Задача10:   х₁=4; 3≤ х₂≤4; (1), (2), (3)

Задача11:   х₁=4; 4≤ х₂≤5; (1), (2), (3)

Решаем Задачу10.

При х₁=4 и х₂=3,

W=8*4+9*3=59

Решение целочисленно, поэтому запомнаем его.

При х₁=4 и х₂=4,

W=8*4+9*4=68

Решение целочисленно, поэтому запомнаем его.

Решаем Задачу11.

При х₁=4,

х₂==

х₂  не удовлетворяет условию, следовательно решений нет.

Список задач пуст.

Таким образом, имем два оптимальных целочисленных решения:

1)  х₁=4; х₂=3; W=8*4+9*3=59

2)  х₁=4; х₂=4; W=8*4+9*4=68

Так как 68>59 то решением примем 2 решение.

Ответ:

х₁*=4

х₂*=4;

F*=68

Общий вывод:

Задача линейного программирования была решена пятью методами