Расчет плана перевозок, при котором общие затраты на перевозку всей продукции, по всем потребителям, будут минимальны

ПОСТАНОВКА ЗАДАЧИ

Имеется 4 склада, содержащие некоторое количество единиц однотипной продукции (Таблица 1), имеется также 5 потребителей, нуждающихся в определенном количестве данной продукции (Таблица 2). При перевозке одной единицы продукции со склада i потребителю j возникают издержки Pij. Величины издержек приведены в Таблице 3. При перевозке K единиц продукции со склада i потребителю j суммарные затраты на перевозку составляют.

Требуется найти такой план перевозок при котором общие затраты на перевозку всей продукции, по всем потребителям, будут минимальны.

Таблица 1

Склад №	Запас единиц продукции
1	17
2	19
3	11
4	13

Таблица 2

Потребитель №	Потребность в единицах продукции
1	5
2	15
3	11
4	9
5	20

Таблица 3

7	10	16	27	19	1
30	18	8	29	15	2
3	18	28	19	13	3
9	12	2	25	21	4
1	2	3	4	5

Склад №
Потребитель №        

1. Проверяем задачу на сбалансированность. Общее число запасов на складах: 60; общая потребность: 60. Задача является закрытой.

2. Метод северо-западного угла (Рисунок 1)

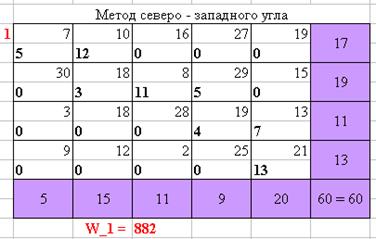
Рисунок 1 – Нахождение оптимального плана перевозок методом северо-западного угла

3. Метод минимального элемента (Рисунок 2)

 

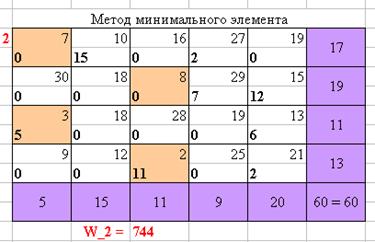
Рисунок 2 – Нахождение оптимального плана перевозок методом минимального элемента

4. Метод двойного предпочтения (Рисунок 3)

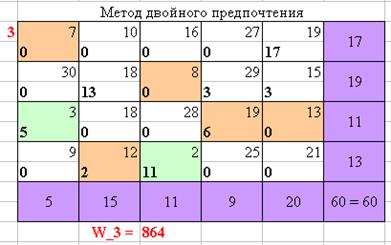
Рисунок 3 – Нахождение оптимального плана перевозок методом двойного предпочтения

5. Метод потенциалов (Рисунок 3 – 6)

Рисунок 4 - Нахождение оптимального плана перевозок методом потенциалов

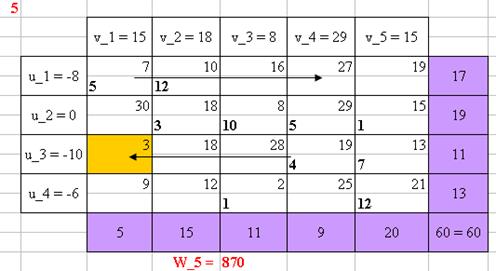
Рисунок 5 - Нахождение оптимального плана перевозок методом потенциалов

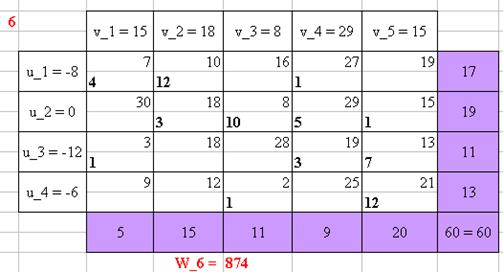
Рисунок 6 - Нахождение оптимального плана перевозок методом потенциалов

6. Венгерский метод (Рисунок 7 -

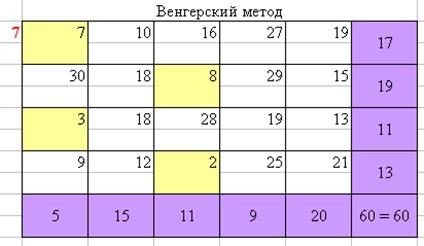
Рисунок 7 – Нахождение оптимального плана перевозок Венгерским методом

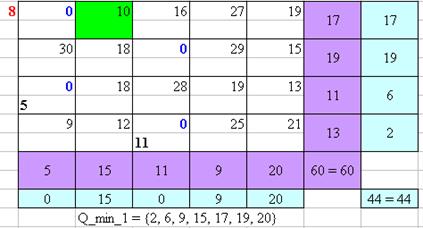
Рисунок 8 – Нахождение оптимального плана перевозок Венгерским методом

    

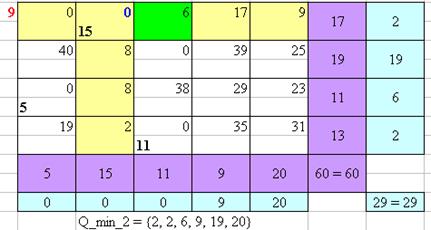
Рисунок 9 – Нахождение оптимального плана перевозок Венгерским методом

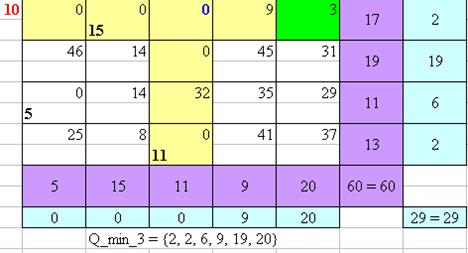
Рисунок 10 – Нахождение оптимального плана перевозок Венгерским методом

  

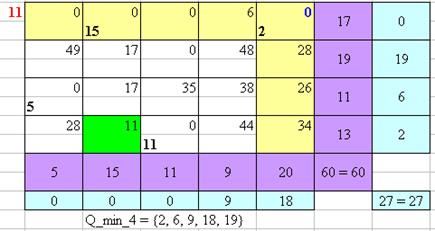
Рисунок 11 – Нахождение оптимального плана перевозок Венгерским методом

        

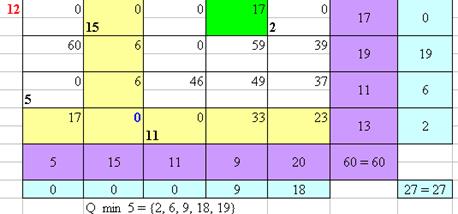
Рисунок 12 – Нахождение оптимального плана перевозок Венгерским методом

                

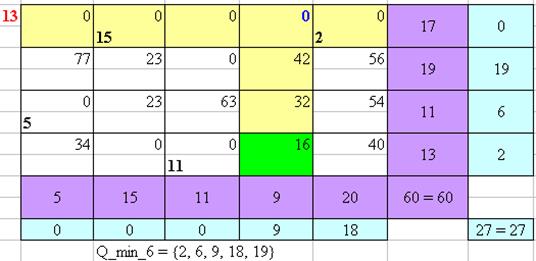
Рисунок 13 – Нахождение оптимального плана перевозок Венгерским методом

          

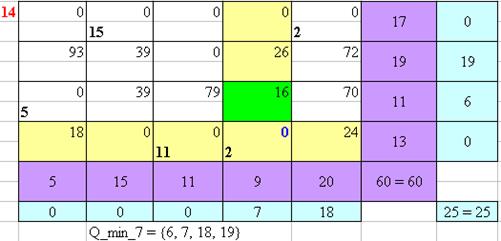
Рисунок 14 – Нахождение оптимального плана перевозок Венгерским методом

            

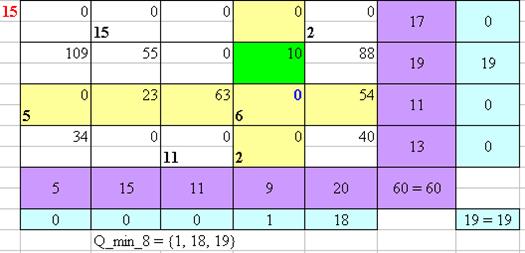
Рисунок 15 – Нахождение оптимального плана перевозок Венгерским методом

    

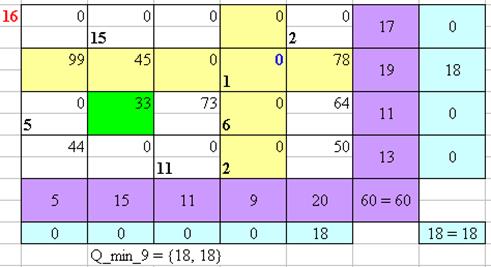
Рисунок 16 – Нахождение оптимального плана перевозок Венгерским методом

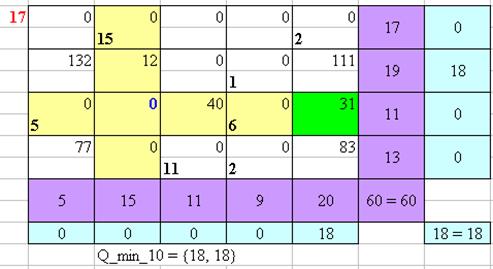
Рисунок 17 – Нахождение оптимального плана перевозок Венгерским методом

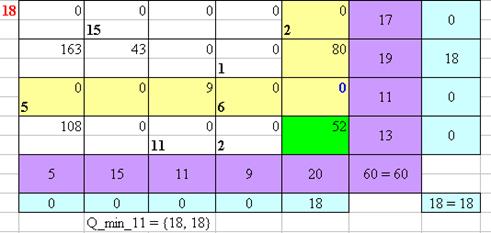
Рисунок 18 – Нахождение оптимального плана перевозок Венгерским методом

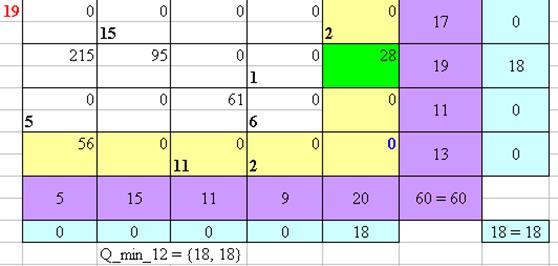
Рисунок 19 – Нахождение оптимального плана перевозок Венгерским методом

  

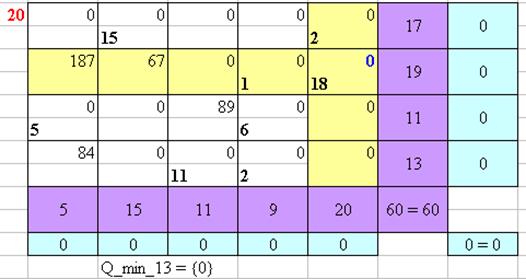
Рисунок 20 – Нахождение оптимального плана перевозок Венгерским методом

Имея старую стоимость перевозок и новое количество единиц груза, получаем значение W = 688.

Таким образом, при решении поставленной задачи всеми выше перечисленными методами (W_{метод северо-западного угла} = 882, W_{метод минимального элемента} = 744, W_{метод двойного предпочтения} = 864, W_{метод потенциалов} = 874, W_{Венгерский метод} = 688), можно сделать заключение, что оптимальным методом решения является Венгерский метод.