Расчет корреляционного поля (потребительские расходы на душу населения), страница 4

Опираясь на данные таблицы, получим следующие значения параметров:

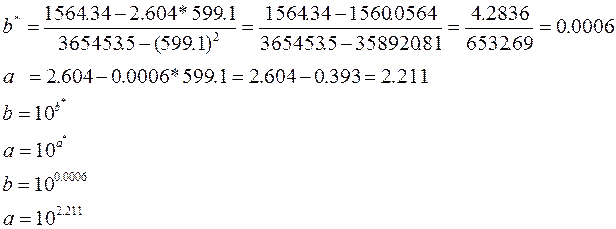
Таким образом, уравнение показательной регрессии будет выглядеть следующим образом:

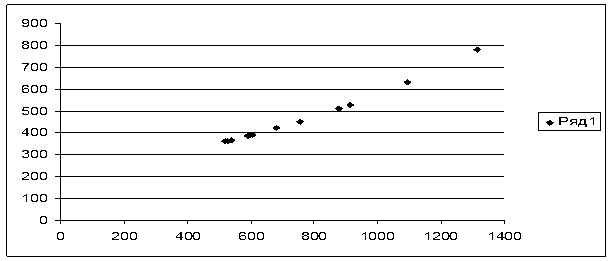
График полученной показательной зависимости на основании таблицы 5

3.  Оценка тесноты связи с помощью показателей корреляции и детерминации.

Вычислим коэффициент корреляции для линейной регрессии: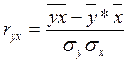

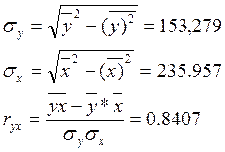
            Таким образом, связь между x и y тесная.

Для логарифмической регрессии значение коэффициента корреляции, вычисленное по аналогии с линейной регрессией, будет иметь следующее значение: 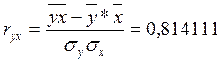- это означает, что связь между x и y тесная.

Коэффициент корреляции этой регрессии ниже, чем коэффициент корреляции линейной регрессии. Значит, линейная регрессия больше подходит для описания взаимодействия  x и y.

Для определения значения коэффициента корреляции для степенной регрессии нам необходимо вычислить значение величин  и . Согласно данным таблицы 3 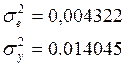. Значит 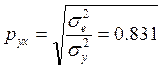- связь средней тесноты.

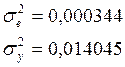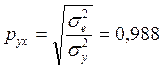Для определения значения коэффициента корреляции для показательной регрессии необходимо вычислить значения  и  для показательной функции. Согласно таблице 5  эти данные: . Значит - связь средней тесноты.

Поскольку величина коэффициента корреляции служит одним из критериев оценки качества модели, то, разумеется, при подборе уравнения регрессии, из всей совокупности регрессии выбирается та, коэффициент корреляции которой выше по сравнению с другими регрессионными уравнениями. В нашем случае такой является логарифмическая.

Вычислим значение коэффициентов детерминации:

Для линейной регрессии . Следовательно, уравнение регрессии объясняет 70,68% дисперсии результативного фактора, а на долю прочих факторов приходится 29,32% ее дисперсии.

Для логарифмической регрессии . Таким образом, если мы аппроксимируем, исходные данные с помощью логарифмической регрессии, то выбранное нами уравнение объяснит 66,28% дисперсии результативного признака, а на долю прочих признаков останется 33,72% ее дисперсии.

Для степенной регрессии: . Как мы видим, данное уравнение (степенное) объясняет 69,01% дисперсии результативного фактора, а на долю прочих факторов останется 30,94% ее дисперсии.

Для показательной регрессии . Как мы видим, данное уравнение (показательное) объясняет 97,61% дисперсии результативного фактора, а на долю прочих факторов останется 2,39% ее дисперсии.

Поскольку величина коэффициента детерминации служит одним из критериев оценки качества модели, то при выборе уравнения регрессии, из всей совокупности регрессий выбирается та, которая в состоянии объяснить большую долю вариации переменной по сравнению с другими регрессионными уравнениями. В нашем случае такой регрессией является показательная.

Аналитическая записка.

Корреляционное поле по данным таблицы 1 не дает возможности предположить, какая зависимость между рассматриваемыми признаками.

Поскольку с помощью коэффициента корреляции, коэффициента детерминации можно оценить статистическую надежность результатов регрессионного моделирования, то сведем полученные результаты в таблицу:

            Сравним полученные по линейной, степенной, показательной и логарифмической регрессии прогнозные значение y.

Вывод: лучше всего исходные данные аппроксимируются с помощью показательной регрессии.