Проектирование квазиэлектронной АТС (монтируемая емкость 350 В), страница 8

,

где V – искомое число линий, определяемое подбором;

W₁ – вероятность занятости всех соединительных путей от входа в первое звено до линии рассматриваемого пучка, включенной в выход последнего звена (вероятность блокировки линии);

Y_P – расчетная нагрузка, приходящаяся на один выход последнего звена.

Вероятность блокировки рассчитывается по формуле:

Величины z₁ и z₂ зависят от числа точек включения линий в выходы блоков и от числа f промежуточных линий между каждым БАЛ и каждым БСЛ. В зависимости от числа f и от числа выходов БСЛ или БИЛ, в которые включается каждая линия, в таблице 8 даны значения z₁ и z_2.

Таблица 8

f	8		4		2		1
Количество точек включения	z1	z2	z1	z2	z1	z2	z1	z2
одна	2	4	1	4	1	2	1	1
две	4	4	2	4	1	4	1	2

В соответствии с числом f определяются значения z₁ и z₂ и рассчитывается W₁. Так как f имеет значение, отличное от приведенных в таблице,

то необходимо вычислить вероятность блокировки W₁ при f ближайшем меньшем к f из таблицы.

для f^’ = 2

z₁ = 1   z₂ = 4

для f^’’ = 4

z₁ = 2   z₂ = 4

После этого искомое значение вероятности блокировки рассчитывается по формуле.

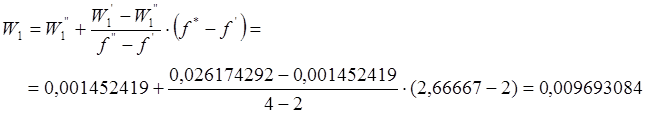¾  Расчет исходящих СЛ к УАТС

Y_И.УАТС = Y_Р = 6,889869563 Эрл

Y_S = 0,16215794 Эрл

Произвольно задаемся числом линий V так, чтобы полученная конечная вероятность была не больше значения 0,01, и определяем величины эффективной доступности D_э:

Пусть V = 14

тогда

В тех случаях, когда доступность принимает не табулированные или дробные значения, следует пользоваться формулой Пальма-Якобеуса:

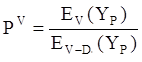
Значения вероятностей числителя и знаменателя определяются по номограмме при заданных нагрузках и числу линий.

Для исходящих СЛ к УАТС она примет вид:

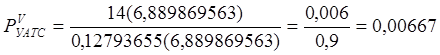
Полученное значение вероятности удовлетворяет поставленному условию, следовательно, произвольно выбранное число V оказалось искомым.

¾  Расчет исходящих СЛ к РАТС

Y_И.РАТС = Y_Р = 3,81874083 Эрл

Y_S =  0,16215794 Эрл

Произвольно задаемся числом линий V так, чтобы полученная конечная вероятность была не больше значения 0,01, и определяем величины эффективной доступности D_э:

Пусть V = 10

тогда

В тех случаях, когда доступность принимает не табулированные или дробные значения, следует пользоваться формулой Пальма-Якобеуса:

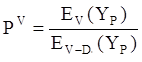
Значения вероятностей числителя и знаменателя определяются по номограмме при заданных нагрузках и числу линий.

Для исходящих СЛ к РАТС она примет вид:

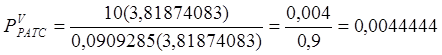
Полученное значение вероятности удовлетворяет поставленному условию, следовательно, произвольно выбранное число V оказалось искомым.

¾  Расчет исходящих СЛ к УАК

Y_И.УАК = Y_Р = 1,774082949 Эрл

Y_S = 0,16215794 Эрл

Произвольно задаемся числом линий V так, чтобы полученная конечная вероятность была не больше значения 0,01, и определяем величины эффективной доступности D_э:

Пусть V = 6

тогда

В тех случаях, когда доступность принимает не табулированные или дробные значения, следует пользоваться формулой Пальма-Якобеуса:

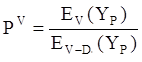
Значения вероятностей числителя и знаменателя определяются по номограмме при заданных нагрузках и числу линий.

Для исходящих СЛ к УАК она примет вид:

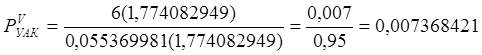
Полученное значение вероятности удовлетворяет поставленному условию, следовательно, произвольно выбранное число V оказалось искомым.

¾  Расчет исходящих ЗЛ

Y_И.ЗЛ = Y_Р = 2,141886366 Эрл

Y_S = 0,16215794 Эрл

Произвольно задаемся числом линий V так, чтобы полученная конечная вероятность была не больше значения 0,01, и определяем величины эффективной доступности D_э:

Пусть V = 7

тогда

В тех случаях, когда доступность принимает не табулированные или дробные значения, следует пользоваться формулой Пальма-Якобеуса:

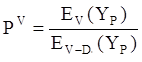
Значения вероятностей числителя и знаменателя определяются по номограмме при заданных нагрузках и числу линий.

Для исходящих СЛ к УАК она примет вид:

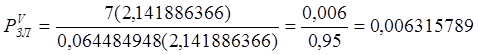
Полученное значение вероятности удовлетворяет поставленному условию, следовательно, произвольно выбранное число V оказалось искомым.

¾  Расчет приемников набора