В задаче рассматривается схема нагружения вала крутящими моментами, вызывающими деформацию кручения, которая измеряется углом закручивания вала. Условие статической прочности вала при кручении состоит в том, что возникающее в сечениях наиболее опасного участка вала максимальное касательное напряжение tmax не должно превышать допускаемого напряжения [t], зависящего от материала вала.
Рекомендуется предварительно изучить следующие вопросы для подготовки к зачету: “Предмет изучения в разделе “Сопротивление материалов”. Расчетная модель. Виды нагрузок. Деформации: упругая и остаточная. Виды простых деформаций. Напряжения: нормальные и касательные. Прочность и жесткость”, “Кручение: напряжение, деформация, расчеты на прочность и жесткость”.
Угол закручивания j (в радианах) на участке вала длиной L (в метрах) рассчитывается по формуле: j = T L / (GJp), где Т – крутящий момент на данном участке вала (Н . м), G – модуль упругости при сдвиге (Па), JP – полярный момент инерции сечения (м4), причем JP = 0,1d4, где d – диаметр вала (в метрах).
В качестве примера рассмотрим решение задачи со следующими исходными данными: размеры вала и величины крутящих моментов Т1 и
26
М 1:2
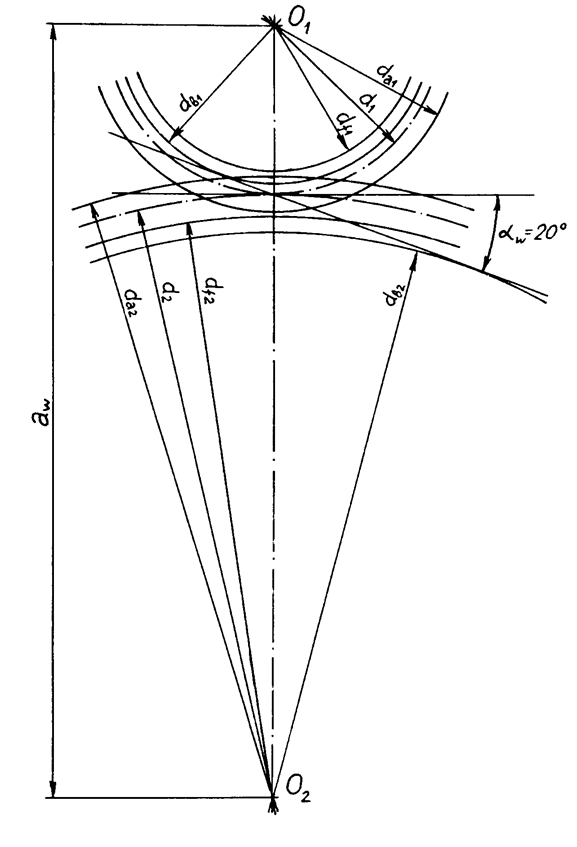
Z1=19 d1=95 мм d2=340 мм p=15,7 мм
Z2=68 da1=105 мм da2=350 мм aw=217,5 мм
m=5 мм df1=82,5 мм df2=327,5 мм
db1=89,3 мм db2=319,5 мм
Рис. 7. Геометрическая картина зубчатого зацепления.
27
Т2 указаны на рис. 8а, допускаемое касательное напряжение [t] = 40 МПа = = 40 . 106 Па, модуль упругости G = 8 . 104 МПа = 8 . 1010 Па.
1. Определяем крутящий момент Т0 в заделке. Условие равновесия вала STi = 0, или T0 – T1 + T2 = 0. Отсюда T0 = T1 – T2 = 2,2 – 0,5 = 1,7 кН.м. Строим эпюру крутящих моментов. На участке A (a = 1,8 м): TA = T0 = = 1,7 кН.м. На участке B (b = 3,2 м): TB = T0 – T1 = 1,7 – 2,2 = – 0,5 кН.м. Опасным является участок A: Tmax = 1,7 кН.м = 1700 Н.м.
2. Вычисляем требуемый
диаметр вала. Максимальное расчетное напряжение при кручении зависит от
максимального крутящего момента Tmax и диаметра d вала: tmax = Tmax / (0,2d3). Отсюда с учетом условия прочности
при кручении tmax 
[t] получаем диаметр: d 
= = 
= 5,97 . 10-2 м = 59,7 мм. Полученный диаметр вала округляем до ближайшего большего значения из ряда Ra40 нормальных линейных размеров по
ГОСТ 6636-69 (приложение 1): d
= 60 мм = 0,06 м.
3. Вычисляем углы закручивания. Предварительно вычисляем полярный момент инерции сечения вала Jp = 0,1d4 = 0,1 . 0,064 = 130 . 10-8 м4 и жесткость вала при деформации кручения GJp = 8 . 1010 . 130 . 10-8 = = 1040 . 102 Н.м2. Углы закручивания: на участке A jA = TA a / (GJp) = = 1700 . 1,8 / (1040 . 102) = 2,94 . 10-2 рад, на участке B: jB = TB b / (GJp) = = – 500 . 3,2 / (1040 . 102) = – 1,54 . 10-2 рад. Строим эпюру углов закручивания, рассчитав угол закручивания в конечной точке участка B jA + jB = 2,94 . 10-2 + (– 1,54 . 10-2) = 1,4 . 10-2 рад. Максимальный угол закручивания jmax = 2,94 . 10-2 рад.
Задача 4
В задаче рассматривается схема нагружения двухопорной балки
28
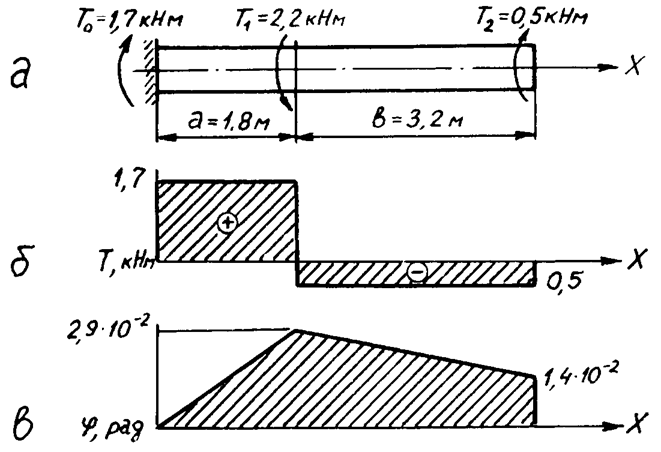
Рис. 8: а – схема нагружения вала, б – эпюра крутящих моментов,
в – эпюра углов закручивания.
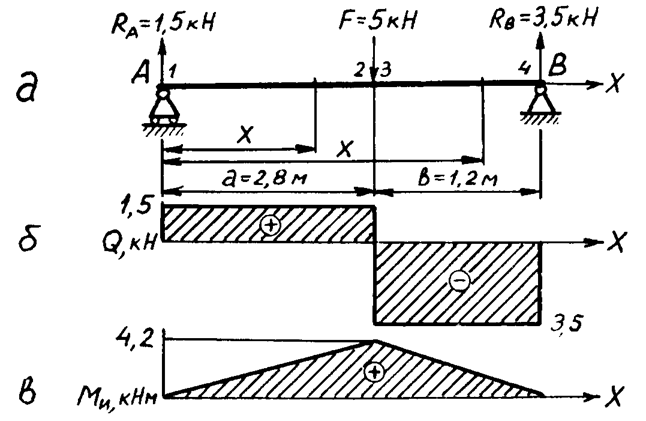
Рис. 9: а – схема нагружения двухопорной балки, б – эпюра поперечной силы Q, в – эпюра изгибающего момента Ми.
29
сосредоточенными силами, вызывающими деформацию изгиба. Условие статической прочности балки при изгибе состоит в том, что возникающее в наиболее опасном сечении балки максимальное нормальное напряжение smax не должно превышать допускаемого напряжения [s], зависящего от материала балки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.